Fichier de rejeu Close
Indication Close
A propos de... Close
Commentaire Close
Systèmes d'Information
- Notions mathématiques
- Calcul relationnel
- Algèbre relationnelle
- Langage de requêtes
- Arbre de requêtes
- Exercices
- Introduction
- Commandes de bases
- Langage de définition de données (LDD)
- Langage de manipulation de données (LMD)
- Types de données
- Exercice
- Dépendances fonctionnelles
- Décomposition de relations
- Inférence logique
- Normalisation
- Aux pays des bières
- Modélisation
- Exercices

© Your Copyright
Aide
Relation binaire
De manière informelle, une relation binaire entre deux ensembles (E,F) est une proposition qui lie entre eux certains éléments de ces deux ensembles.
Nous présentons ici la définition d’une relation binaire en introduisant différentes notions de base :
- définition mathématique d’une relation binaire
- domaine et image d’une relation binaire
- sémantique d’une relation binaire (entre des employés et des sociétés)
- diagramme sagittal d’une relation binaire
- cardinalité d’une relation binaire
et en appliquant ces notions sur un simple exemple d’employés dans des sociétés à l’aide des formalismes de modélisation Entité-Association et UML .
Une relation binaire \(R\) entre deux ensembles (\(E,F\)) est définie par un sous-ensemble (une partie) du produit cartésien (\(R \subset E \times F\)).
- Autrement dit une relation binaire est une collection de couples, \((x, y)\) tel que :
- \(x \in E\): la première composante du couple est dans \(E\)
- \(y \in F\) : la seconde dans \(F\)
Si le couple \((x, y) \in R\) on dit que (l’élément) x est en relation avec (l’élément) y.
- La relation entre les deux éléments s’exprime :
- en notation infixée : \(xRy\)
- en notation préfixée : \(Rxy\) ou encore \(R(x,y)\)
Le domaine de définition de la relation binaire est l’ensemble des éléments de E qui sont en relation avec des éléments de F :
- \(dom(R) = \{ x \in E \mid \exists y \in F,(x,y) \in R \}\)
L’image de la relation binaire est l’ensemble des éléments (valeurs) de F mis en relation avec le domaine de définition :
- \(image(R) = \{ y \in Y \mid \exists x \in E,(x,y) \in R \}\)
Soit l’ensemble des employés et des sociétés
- \(employes = \{e_1,e_2,e_3,e_4,e_5 \}\)
- \(societes = \{ s_1,s_2,s_3,s_4 \}\)
La relation travailler est représentée par l’ensemble des couples :
- \(travailler = \{ (e_1,s_1),(e_2,s_1), (e_2,s_2),(e_3,s_2),(e_4,s_2),(e_4,s_3)\}\)
- une société (\(s_1,s_2\)) peut avoir plusieurs employés (ça parait normal !)
- un employé (\(e_2,e_4\)) peut travailler dans plusieurs sociétés (c’est possible !)
- il existe des employés (\(e_5\)) qui ne travaillent pas (malheureusement !)
- il existe des sociétés (\(s_4\)) qui n’ont pas d’employés (c’est bizarre !)
La sémantique de la relation définit le sens (de l’ensemble de départ à l’ensemble d’arrivée) :
- les employés travaillent pour une société.
En inversant le sens de la relation on obtiendrait :
- les sociétés qui font travailler des employés.
Une relation peut être définie par un verbe d’action qui relie deux entités (sujet et complément).
Le verbe conjugué définit l’action, le lien, la sémantique de l’association.
Pour représenter graphiquement la relation, on peut utiliser un diagramme sagittal (du latin sagitta : flèche)
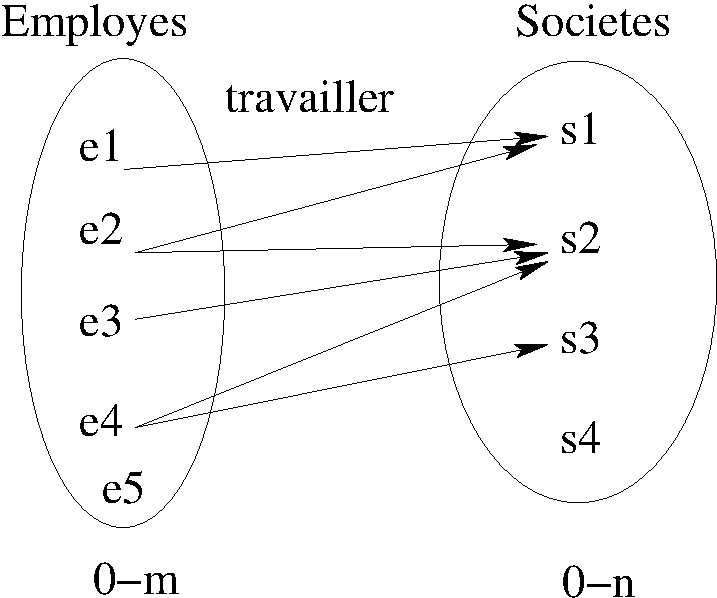
Dans cette représentation on remarquera les notations :
- \((0-m)\) sous l’ensemble des employés
- \((0-n)\) sous l’ensemble des sociétés
Ces notations indiquent le nombre d’éléments d’un ensemble qui pourront être mis en relation avec les éléments de l’autre ensemble impliqué dans la relation binaire. C’est ce qu’on appelle la cardinalité de la relation.
Dans ce cas il peut y avoir plusieurs employés (0-m) à travailler dans une société et un employé peut travailler dans plusieurs sociétés (0-n).
Cette notation représente le nombre d’éléments d’un ensemble qui peuvent être mis en jeu avec un élément de l’autre ensemble dans la relation binaire :
- il existe dans l’ensemble des employés des éléments (\(e_5\)) qui ne travaillent pas \((0-...)\)
- un employé (\(e_2,e_4\)) peut travailler dans plusieurs sociétés \((...-m)\)
- il existe dans l’ensemble des sociétés des éléments (\(s_4\)) qui n’ont pas d’employés \((0-...)\)
- une société (\(s_1,s_2\)) peut faire travailler plusieurs employés \((...-n)\))
Pour les associations binaires, la cardinalité minimale (resp. maximale) est le nombre minimum (resp. maximum) d’occurrences de l”entité d’arrivée associées à une occurrence de l”entité de départ.
Cardinalité d’une association dans le modèle Entité-Association :
Dans l’exemple de la figure ci-dessus les cardinalités représentent les contraintes suivantes :
- les employés peuvent ne pas travailler ou être dans une ou plusieurs sociétés \((0,m)\)
- une société peut n’avoir aucun employé ou en avoir un ou plusieurs \((0,n)\)
On modélise ici les employés qui peuvent éventuellement travailler dans des sociétés qui peuvent éventuellement avoir des employés.
Dans la notation UML les cardinalités sont inversées par rapport à la représentation du modèle Entité-Association.
La liaison entre l’ensemble et la relation est notée (\(..\)) et une cardinalité multiple est représentée par une étoile (*).
Ainsi le diagramme UML de la figure suivante :
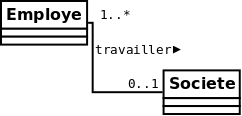
représentera les contraintes suivantes :
- un employé travaille au plus dans une société
- une société fait travailler au moins un employé
On modélise donc les employés qui peuvent éventuellement travailler dans une société qui a au moins un employé.
