Fichier de rejeu Close
Indication Close
A propos de... Close
Commentaire Close
Systèmes d'Information
- Notions mathématiques
- Calcul relationnel
- Algèbre relationnelle
- Langage de requêtes
- Arbre de requêtes
- Exercices
- Introduction
- Commandes de bases
- Langage de définition de données (LDD)
- Langage de manipulation de données (LMD)
- Types de données
- Exercice
- Dépendances fonctionnelles
- Décomposition de relations
- Inférence logique
- Normalisation
- Aux pays des bières
- Modélisation
- Exercices
© Your Copyright
Aide
Aux pays des bières
- On propose dans cet exercice de travailler sur une base de données en formulant la recherche d’information :
- sous forme d’arbre de requêtes
- en langage SQL
à partir de questions exprimées en langage naturel (français).
Le modèle de données sur lequel on travaillera représentera très schématiquement :
- les bars qui servent des bières
Cette phrase (sujet-verbe-complément) permet d’identifier deux entités (bars,bières) reliées par un verbe représentant une association entre ces deux entités.
Nous verrons plus en détail dans le chapitre « Modélisation » ces notions d’Entité-Association très utiles pour proposer une structuration de bases de données.
Modèle de données
En partant de cette simple phrase représentant le « monde » à modéliser :
- les bars qui servent des bières
On peut émettre les hypothèses suivantes :
- un bar peut servir plusieurs bières
- une bière peut-être servie dans plusieurs bars
Ces hypothèses signifient que l’on a à faire à une association plusieurs à plusieurs entre les deux entités (bars,bières).
Cette situation nécessite de « réifier » le verbe (le transformer en une entité) afin de transformer l’association plusieurs à plusieurs en deux associations un à plusieurs.
On peut donc se baser sur le modèle de données :
- un bar propose plusieurs services
- une bière peut être proposée dans plusieurs services
qui fait apparaître l’entité services (sujet-verbe-complément)
On peut également conjuguer différemment les phrases :
- chaque service est proposé dans un bar
- chaque service concerne une bière
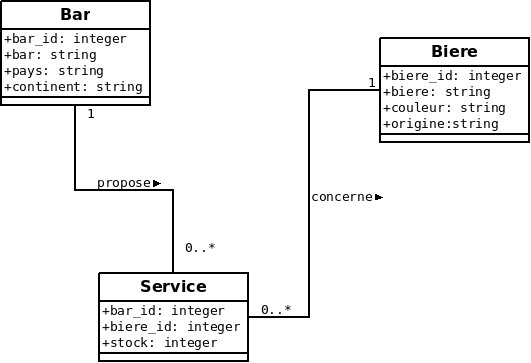
A partir de ces phrases on peut représenter ce modèle de données en utilisant le formalisme UML :
A partir de ce modèle de données on peut créer les tables qui correspondent aux entités de ce modèle.
Représentation, en SQL, du modèle de données à étudier.
A partir du modèle de données UML on peut structurer la base de données en trois tables :
- bars(bar_id,bar,pays,continent)
- services(bar_id,bar,biere_id,stock)
- bieres(biere_id,biere,couleur,origine)
où les associations sont mises en oeuvre par des clés étrangères qui apparaissent sur les entités de cardinalité supérieure à 1 (du côté plusieurs de l’association).
CREATE TABLE bars (
bar_id INTEGER NOT NULL PRIMARY KEY,
-- bar_id INTEGER NOT NULL PRIMARY KEY AUTOINCREMENT,
bar TEXT,
pays TEXT,
continent TEXT
);
CREATE TABLE bieres (
biere_id INTEGER NOT NULL PRIMARY KEY,
-- biere_id INTEGER NOT NULL PRIMARY KEY AUTOINCREMENT,
biere TEXT,
couleur TEXT,
origine TEXT
);
CREATE TABLE services (
bar_id INTEGER NOT NULL,
biere_id INTEGER NOT NULL,
stock SMALLINT,
PRIMARY KEY (bar_id,biere_id),
FOREIGN KEY (bar_id) REFERENCES bars(bar_id) ON DELETE CASCADE,
FOREIGN KEY (biere_id) REFERENCES bieres(biere_id) ON DELETE CASCADE
);
On pourra vérifier l’état de la base de données en formulant les requêtes pour retrouver toutes les informations des trois tables :
Arbres de requêtes
L’objectif de ces exercices est de savoir représenter sous forme d’arbre de requêtes, la recherche d’informations à partir :
- d’une seule table (projection et restriction)
- de plusieurs tables (jointures)
- des opérations ensemblistes (union,intersection,différence)
- de formulation de division relationnelle
- des fonctions d’agrégats
- des regroupements dans un ensemble avec restriction sur les groupements
Savoir formuler, sous forme d’arbre, une requête sur une table en appliquant des :
-
Vérification du contenu des tables de la base de données
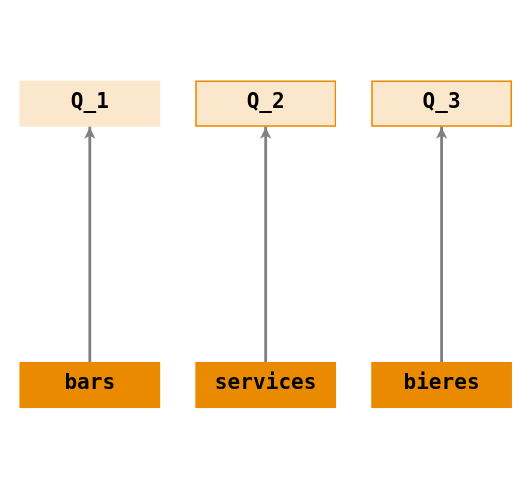
Construire les arbres de requêtes répondant aux questions :
- \(Q_1\) : « quel est le contenu de la table
bars - \(Q_2\) : « quel est le contenu de la table
services - \(Q_3\) : « quel est le contenu de la table
bieres
Votre réponse :
Arbre de requêtes : graph6.jsonTables
Opérateurs unaires
Opérateurs binaires
Vue d'ensemble Une solution possible :
Récupérer les éléments (
b) de l’ensemble (bars) : \(\displaystyle Q_1 = bars(b)\)Récupérer les éléments (
s) de l’ensemble (services) : \(\displaystyle Q_2 = services(s)\)Récupérer les éléments (
b) de l’ensemble (bieres) : \(\displaystyle Q_3 = bieres(b)\)
- \(Q_1\) : « quel est le contenu de la table
-
Projection
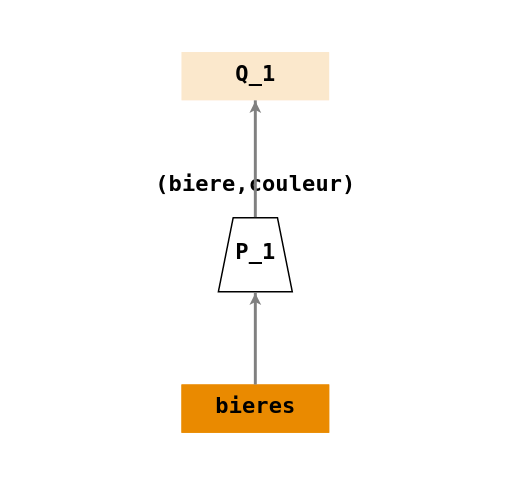
Construire un arbre de requêtes répondant à la question :
- \(Q_1\) : « Rechercher le nom et la couleur des bières ».
Votre réponse :
Arbre de requêtes : graph10.jsonTables
Opérateurs unaires
Opérateurs binaires
Vue d'ensemble Une solution possible :
Ecriture en algèbre relationnelle :
- \(Q_1 = \Pi_{(biere,couleur)}(bieres)\)
On applique une projection (\(\Pi\)) sur les colonnes
(biere,couleur)de la tablebieres.Arbre de requêtes :
-
Restriction
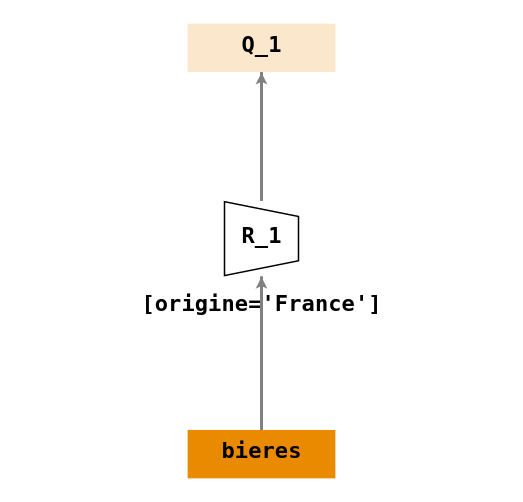
Construire un arbre de requêtes répondant à la question :
- \(Q_1\) : « Rechercher les bières d’origine française ».
Votre réponse :
Arbre de requêtes : graph14.jsonTables
Opérateurs unaires
Opérateurs binaires
Vue d'ensemble Une solution possible :
Ecriture en algèbre relationnelle :
- \(Q_1 = \sigma_{[origine = 'France']}(bieres)\)
On applique une restriction (\(\sigma\)) avec la condition
[origine = 'France']sur la tablebieres.Arbre de requêtes :
-
Projection et restriction
Construire un arbre de requêtes répondant à la question :
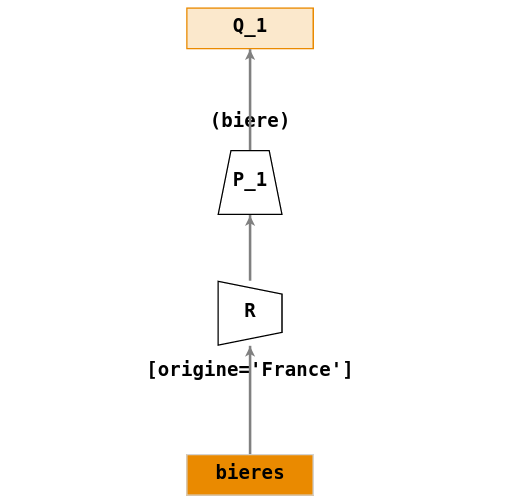
- \(Q_1\) : « Rechercher le nom des bières françaises ».
Votre réponse :
Arbre de requêtes : graph18.jsonTables
Opérateurs unaires
Opérateurs binaires
Vue d'ensemble Une solution possible :
Ecriture en algèbre relationnelle :
- \(Q_1 = \Pi_{(biere)}(\sigma_{[origine='France']}(bieres))\)
On applique une projection (\(\Pi\)) sur la colonne
biereet une restriction (\(\sigma\)) sur la condition[origine='France']de la tablebieres.Arbre de requêtes :
-
Connecteur logique
Construire un arbre de requêtes répondant à la question :
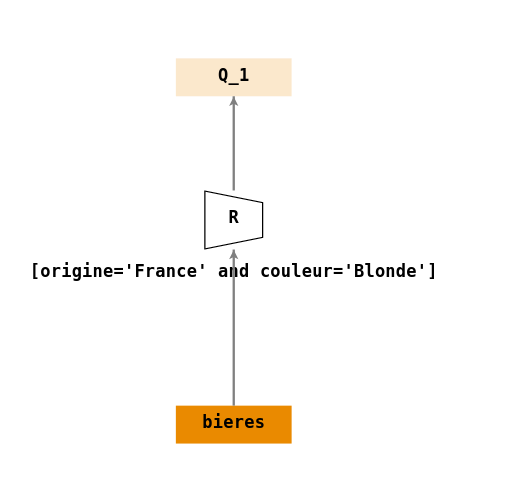
- \(Q_1\) : « Rechercher les bières blondes françaises ».
Votre réponse :
Arbre de requêtes : graph22.jsonTables
Opérateurs unaires
Opérateurs binaires
Vue d'ensemble Une solution possible :
Ecriture en algèbre relationnelle :
- \(Q_1 = \sigma_{[origine='France' \land couleur='Blonde']}(bieres)\).
On vérifie (\(\sigma\)) que les bières sont d’origine française (
origine='France') et (\(\land\)) qu’elles sont de couleur blonde (couleur='Blonde')Arbre de requêtes :
-
Connecteurs logiques
Construire un arbre de requêtes répondant à la question :
- \(Q_1\) : « Rechercher le nom et la couleur des bières françaises blondes et les bières brunes ».
Votre réponse :
Arbre de requêtes : graph26.jsonTables
Opérateurs unaires
Opérateurs binaires
Vue d'ensemble Une solution possible :
Ecriture en algèbre relationnelle :
- \(Q_1 = \sigma_{[origine='France' \land couleur='Blonde' \lor couleur='Brune']}(bieres)\)
On vérifie (\(\sigma\)) sur la table
bieresqu’elles sont d’origine française et (\(\land\) : et logique) de couleur blonde ou (\(\lor\): ou logique) que la couleur des bières est brune.Arbre de requêtes :
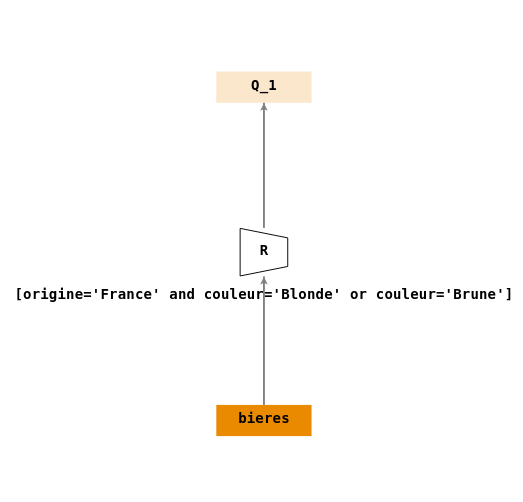
Attention à la priorité du connecteur logique \(\land\) sur le \(\lor\) (de même que la multiplication l’est sur l’addition).
- La requête :
- \(Q_1 = \sigma_{[origine='France' \lor couleur='Blonde' \land couleur='Brune']}(bieres)\)
donnerai comme résultat … les bières françaises (il ne peut exister des bières blonde et brune à la fois).
- Remarque : on peut modifier la priorité en parenthésant des parties de la restriction :
- \(Q_1 = \sigma_{[origine='France' \land (couleur='Blonde' \lor couleur='Brune')]}(bieres)\)
donnera comme résultat les bières françaises et les bières de couleur blonde ou brune.
Savoir représenter, sous forme d’arbre, une requête sur plusieurs tables de la base de données « Aux pays des bières ».
-
Produit cartésien et restriction
Construire un arbre de requêtes répondant à la question :
- \(Q_1\) : « Rechercher les bars qui servent de la bière ».
Votre réponse :
Arbre de requêtes : graph31.jsonTables
Opérateurs unaires
Opérateurs binaires
Vue d'ensemble Une solution possible :
Ecriture en algèbre relationnelle :
- \(IJ_1 = \Join_{[bars.bar\_id=services.bar\_id]}(bars,services)\)
- \(IJ_2 = \Join_{[IJ_1.biere\_id=bieres.biere\_id]}(IJ_1,bieres)\)
- \(Q_1 = IJ_2\)
On réalise ici deux jointures (\(\Join\)) entre les tables
bars,servicespuis une jointure entre le résultat obtenu (\(IJ_1\)) et la tablebieres.L’ordre d’éxecution des jointures (\(IJ_1\) avant ou après \(IJ_2\)) dépendra de l’état de la base de données (nombre d’enregistrements dans les tables, utilisation d’index sur colonnes …) et sera déterminé par l’optimiseur de requêtes du SGBD Relationnel utilisé.
Remarque :
une jointure est une combinaison de produit cartésien et de restriction, on peut les représenter à l’aide de ces opérateurs :
- \(IJ_1 = \sigma_{[bars.bar\_id=services.bar\_id]}(\times(bars,services))\)
- \(IJ_2 = \sigma_{[IJ_1.biere\_id=bieres.biere\_id]}(\times(IJ_1,bieres))\)
Arbre de requêtes :
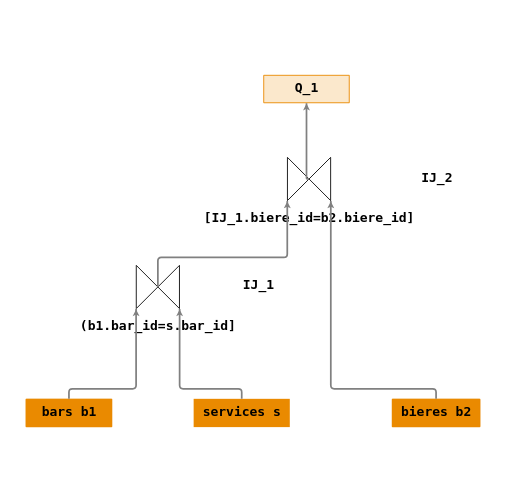
Le lecteur pourra vérifier qu’on obtient le même résultat en modifiant l’ordre d’éxecution des jointures dans l’arbre de requêtes.
-
Création de vue
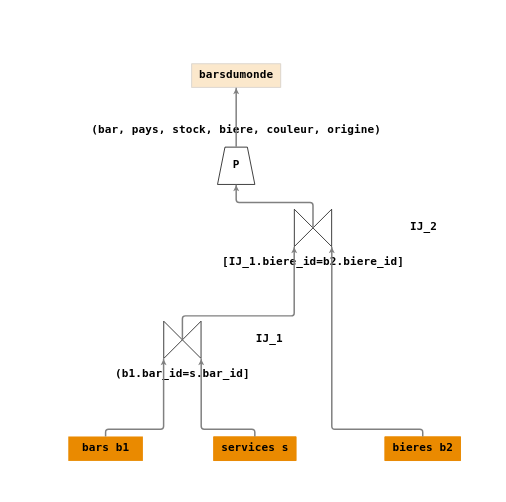
Construire un arbre de requêtes pour créer une vue barsdumonde sur les informations “métier” (sans les clés
bar_id,biere_id) des « bars qui servent de la bière ».Votre réponse :
Arbre de requêtes : graph35.jsonTables
Opérateurs unaires
Opérateurs binaires
Vue d'ensemble Une solution possible :
Ecriture en algèbre relationnelle :
- \(IJ_1 = \Join_{[bars.bar_id=services.bar_id]}(bars,services)\)
- \(IJ_2 = \Join_{[NJ_1.biere_id=bieres.biere_id]}(IJ_1,bieres)\)
- \(P = \Pi_{(bar,pays,stock,biere,couleur,origine)}(IJ_2)\)
- \(barsdumonde=P\)
Arbre de requêtes :
Savoir formuler, sous forme d’arbre, des opérations ensemblistes (\(\cup,\cap,\setminus\)) sur le modèle de données « Aux pays des bières ».
-
Union
Construire un arbre de requêtes répondant à la question :
- \(Q_1\) : « récupérer les noms des pays ou se trouvent des bars et ceux des origines de fabrication des bières ».
Votre réponse :
Arbre de requêtes : graph40.jsonTables
Opérateurs unaires
Opérateurs binaires
Vue d'ensemble Une solution possible :
Ecriture en algèbre relationnelle :
- \(P_1 = \Pi_{(pays)}(bars)\)
- \(P_2 = \Pi_{(origine)}(bieres)\)
- \(U_1 = \cup(P_1,P_2)\)
- \(Q_1 = U_1\)
Arbre de requêtes :
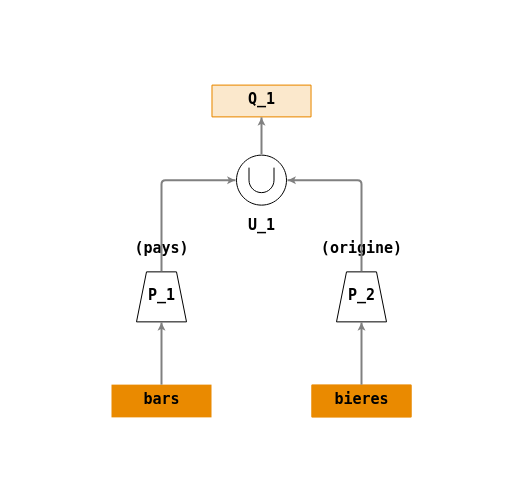
On applique d’abord une projection (\(\Pi\)) sur les colonnes
paysde tablebarsetoriginede la tablebierespour pouvoir mettre en oeuvre l’opération ensembliste d’union (\(\cup\)).Les opérations ensemblistes sont des opérateurs binaires qui doivent avoir pour chaque entrée (opérande) le même nombre d’attributs, chacun étant défini sur le même domaine.
-
Intersection
Construire un arbre de requêtes répondant à la question :
- \(Q_1\) : « Rechercher les noms des pays qui produisent de la bière et qui ont des bars ».
Votre réponse :
Arbre de requêtes : graph44.jsonTables
Opérateurs unaires
Opérateurs binaires
Vue d'ensemble Une solution possible :
Ecriture en algèbre relationnelle :
- \(P_1 = \Pi_{(origine)}(bieres)\)
- \(P_2 = \Pi_{(pays)}(bars)\)
- \(I_1 = \cap(P_1,P_2)\)
- \(Q_1 = I_1\)
Arbre de requêtes :
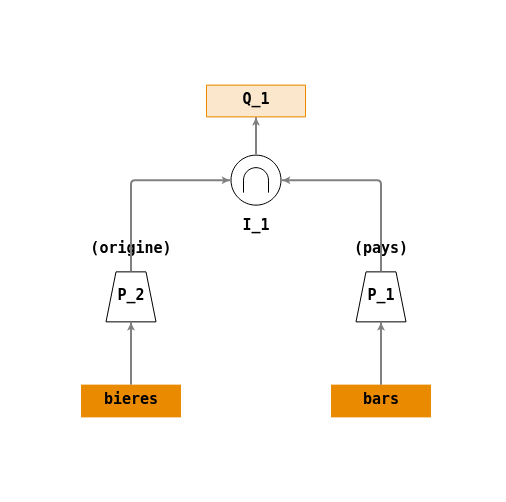
On applique d’abord une projection (\(\Pi\)) sur les colonnes
originede tablebieresetpaysde la tablebarspour pouvoir appliquer l’opération ensembliste d’intersection (\(\cap\)).Les opérations ensemblistes sont des opérateurs binaires qui doivent avoir pour chaque entrée (opérande) le même nombre d’attributs, chacun étant défini sur le même domaine.
-
Différence
Construire un arbre de requêtes répondant à la question :
- \(Q_1\) : « récupérer les noms des pays fabriquant de la bière mais n’ayant pas de bars ».
Votre réponse :
Arbre de requêtes : graph48.jsonTables
Opérateurs unaires
Opérateurs binaires
Vue d'ensemble Une solution possible :
Ecriture en algèbre relationnelle :
- \(P_1 = \Pi_{(origine)}(bieres)\)
- \(P_2 = \Pi_{(pays)}(bars)\)
- \(E_1 = \setminus(P_1,P_2)\)
- \(Q_1 = E_1\)
Arbre de requêtes :
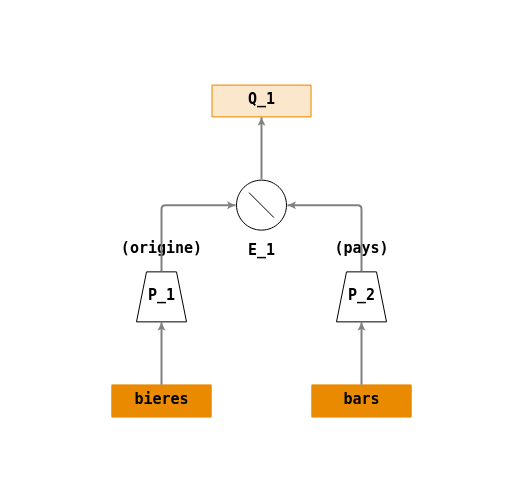
On applique d’abord une projection (\(\Pi\)) sur les colonnes
paysde tablebarsetoriginede la tablebierespour pouvoir appliquer l’opération ensembliste de différence (\(\displaystyle {\setminus}\)).Les opérations ensemblistes sont des opérateurs binaires qui doivent avoir pour chaque entrée (opérande) le même nombre d’attributs, chacun étant défini sur le même domaine.
Contrairement aux opérations ensemblistes d’union et d’intersection, la différence n’est pas commutative.
Savoir répondre « Aux pays des bières » à des questions du type :
- “trouve-moi les \(x\) qui sont associés à tous (\(\forall\)) les \(y\)“
Dans notre cas savoir, par exemple, représenter sous forme d’arbre de requêtes la question :
- “trouver les bars qui servent toutes les bières
-
DOUBLE NEGATION (1/2)
Construire un arbre de requêtes répondant à la question :
- \(Q_1\) : « quels sont les identifiants des bars qui servent toutes les bières ? ».
Votre réponse :
Arbre de requêtes : graph53.jsonTables
Opérateurs unaires
Opérateurs binaires
Vue d'ensemble Une solution possible :
Ecriture en algèbre relationnelle :
- \(P_1 = \Pi_{(bar\_id,biere\_id)}(services)\)
- \(P_2 = \Pi_{(biere\_id)}(bieres)\)
- \(D = \div(P_1,P_2)\)
- \(Q = D\)
Arbre de requêtes :
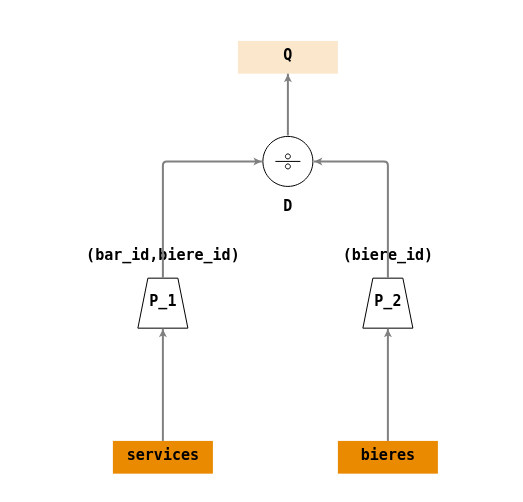
On peut représenter le symbole de division relationnelle dans un arbre de requête. Cependant il faut garder à l’esprit que cet opérateur n’existe pas en SQL, mais qu’on pourra le mettre en œuvre, par exemple à l’aide d’une double négation (
NOT EXISTSimbriqués).De manière générique on peut formuler la division relationnelle pour récupérer dans l’ensemble
S(S[X,Y]) les éléments qui sont liés à tous ceux de l’ensembleT(T[Y]) par l’information (Y) par l’écriture de l’expression algèbrique :- \(\div(\Pi_{(X,Y)}(S),\Pi_{(Y)}(T))\)
-
DOUBLE NEGATION (2/2)
Construire un arbre de requêtes répondant à la question :
- \(Q_1\) : « quels sont les noms des bars qui servent toutes les bières ? ».
Votre réponse :
Arbre de requêtes : graph57.jsonTables
Opérateurs unaires
Opérateurs binaires
Vue d'ensemble Une solution possible :
Ecriture en algèbre relationnelle :
- \(P_1 = \Pi_{(bar\_id,biere\_id)}(services)\)
- \(P_2 = \Pi_{(biere\_id)}(bieres)\)
- \(D = \div(P_1,P_2)\)
- \(IJ_1 = \Join_{[D.bar\_id=bars.bar\_id]}(D,bars)\)
- \(P_3 = \Pi_{(bar)}(IJ_1)\)
- \(Q_1 = P_3\)
Arbre de requêtes :
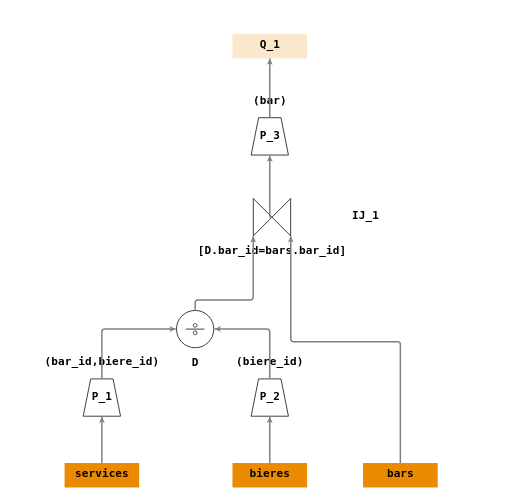
On peut représenter le symbole de division relationnelle dans un arbre de requête. Cependant il faut garder à l’esprit que cet opérateur n’existe pas en SQL, mais qu’on pourra le mettre en œuvre, par exemple à l’aide d’une double négation (
NOT EXISTSimbriqués).De manière générique on peut formuler la division relationnelle pour récupérer dans l’ensemble
S(S[X,Y]) les éléments qui sont liés à tous ceux de l’ensembleT(T[Y]) par l’information (Y) par l’écriture de l’expression algèbrique :- \(\div(\Pi_{(X,Y)}(S),\Pi_{(Y)}(T))\)
-
GROUP BY, HAVING, COUNT (1/3)
Construire un arbre de requêtes répondant à la question :
- \(Q_1\) : « quels sont les identifiants des bars qui servent toutes les bières ? ».
Votre réponse :
Arbre de requêtes : graph61.jsonTables
Opérateurs unaires
Opérateurs binaires
Vue d'ensemble Une solution possible :
- \(P_1 = \Pi_{(bar\_id,biere\_id)}(services)\)
- \(P_2 = \Pi_{(biere\_id)}(bieres)\)
- \(D = \div(P_1,P_2)\)
- \(Q_1 = \Pi_{(bar\_id)}(D)\).
Arbre de requêtes :
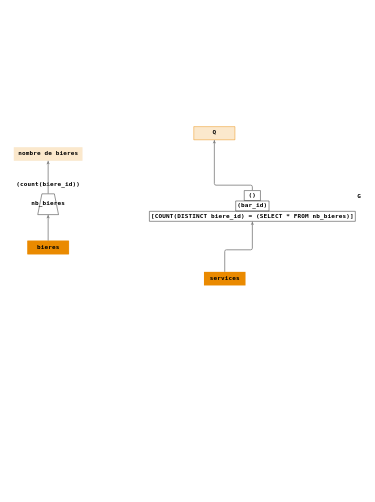
L’opération de division relationnelle n’existe pas en SQL, mais on peut le mettre en œuvre en appliquant des fonctions d’agrégats sur des regroupements.
- En effet on peut compter le nombre de bières différentes servies par bar (
GROUP BY) et ne retenir (conditionHAVING) que ceux pour lesquels le nombre de bières est égal au nombre total de bières existantes dans la base de données. On peut donc reformuler la question : - trouver les identifiants des bars qui servent un nombre de bières différentes qui soit égal au nombre total de bières de la base de données.
Dans ce cas, on peut reformuler la division relationnelle par l’expression algébrique :
- \(nb\_bieres=\Pi_{count(biere\_id)}(bieres)\)
- \(G = G_{[count(biere\_id)=nb\_bieres]}^{(bar\_id)}(services)\).
- \(Q_1 = \Pi_{(bar\_id)}(G)\).
Le symbole \(G\) représente l’opérateur de regroupement appliqué sur la table
servicesavec :- en exposant : attributs de groupement (
GROUP BY) - en indice : critère de restriction (
HAVING) sur les groupements.
Cette expression algébrique suppose qu’on élimine les doublons.
-
GROUP BY, HAVING, COUNT (2/3)
Construire un arbre de requêtes répondant à la question :
- \(Q_1\) : « quels sont les noms des bars qui servent toutes les bières ? ».
Votre réponse :
Arbre de requêtes : graph65.jsonTables
Opérateurs unaires
Opérateurs binaires
Vue d'ensemble bar Bar du Coin Une solution possible :
Ecriture en algèbre relationnelle :
- \(P_1 = \Pi_{(bar\_id,biere\_id)}(services)\)
- \(P_2 = \Pi_{(biere\_id)}(bieres)\)
- \(D = \div(P_1,P_2)\)
- \(IJ = \Join_{[D.bar\_id=bars.bar\_id]}(D,bars)\)
- \(P = \Pi_{(bar)}(IJ_1)\)
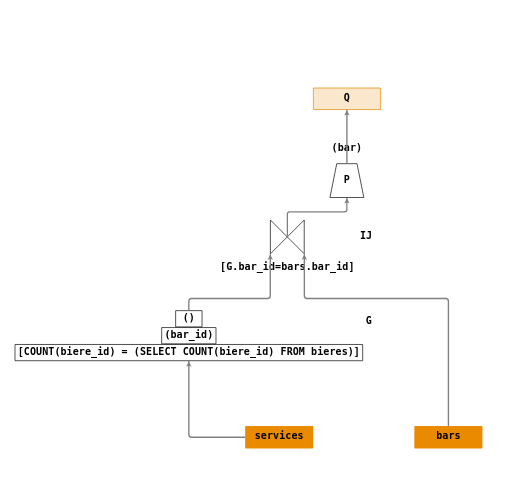
L’opération de division relationnelle n’existe pas en SQL, mais on peut le mettre en œuvre en appliquant des fonctions d’agrégats sur des regroupements.
- En effet on peut compter le nombre de bières différentes servies par bar (
GROUP BY) et ne retenir (conditionHAVING) que ceux pour lesquels le nombre de bières est égal au nombre total de bières existantes dans la base de données. On peut donc reformuler la question : - trouver les identifiants des bars qui servent un nombre de bières différentes qui soit égal au nombre total de bières de la base de données.
Dans ce cas, on peut reformuler la division relationnelle par l’expression algébrique :
- \(IJ = \Join_{[bars.bar\_id=services.bar\_id]}(bars,services)\)
- \(nb\_bieres=\Pi_{count(biere\_id)}(bieres)\)
- \(G = G_{[count(biere\_id)=nb\_bieres]}^{(bar)}(IJ)\).
- \(Q_1 = \Pi_{(bar)}(G)\).
Le symbole \(G\) représente l’opérateur de regroupement appliqué sur la table
servicesavec :- en exposant : attributs de groupement (
GROUP BY) - en indice : critère de restriction (
HAVING) sur les groupements.
Cette écriture supposant qu’on élimine les doublons.
Arbre de requêtes :
-
GROUP BY, HAVING, COUNT (3/3)
Construire un arbre de requêtes répondant à la question :
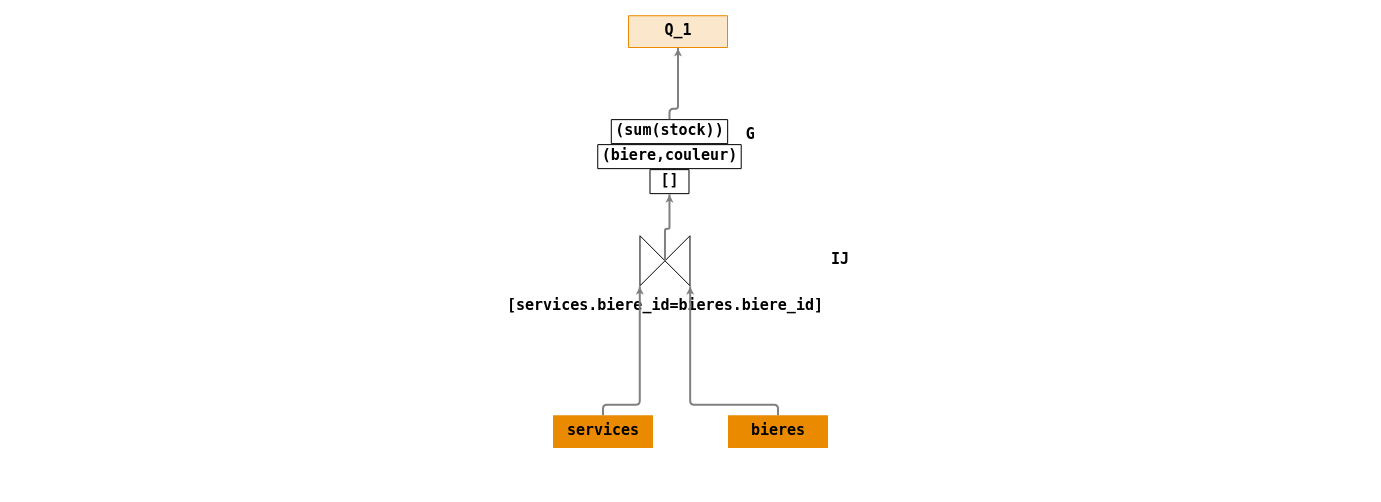
- \(Q_1\) : « nom des bars qui servent toutes les bières et somme de leur stock de bières ».
Votre réponse :
Arbre de requêtes : graph70.jsonTables
Opérateurs unaires
Opérateurs binaires
Vue d'ensemble Une solution possible :
Ecriture en algèbre relationnelle :
- \(P_1 = \Pi_{(bar\_id,biere\_id)}(services)\)
- \(P_2 = \Pi_{(biere\_id)}(bieres)\)
- \(D = \div(P_1,P_2)\)
- \(IJ = \Join_{[D.bar\_id=bars.bar\_id]}(D,bars)\)
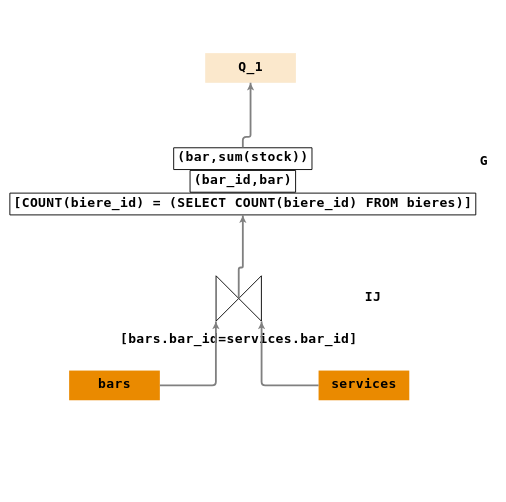
- \(P = \Pi_{(bar,sum(stock))}(IJ_1)\)
L’opération de division relationnelle n’existe pas en SQL, mais on peut le mettre en œuvre en appliquant des fonctions d’agrégats sur des regroupements.
- En effet on peut compter le nombre de bières différentes servies par bar (
GROUP BY) et ne retenir (conditionHAVING) que ceux pour lesquels le nombre de bières est égal au nombre total de bières existantes dans la base de données. On peut donc reformuler la question : - trouver les identifiants des bars qui servent un nombre de bières différentes qui soit égal au nombre total de bières de la base de données.
Dans ce cas, on peut reformuler la division relationnelle par l’expression algébrique :
- \(IJ = \Join_{[bars.bar\_id=services.bar\_id]}(bars,services)\)
- \(nb\_bieres=\Pi_{count(biere\_id)}(bieres)\)
- \(G = G_{[count(biere\_id)=nb\_bieres]}^{(bar)}(IJ_1)\).
- \(Q_1 = \Pi_{(bar,sum(stock))}(G)\).
Le symbole \(G\) représente l’opérateur de regroupement appliqué sur la table
servicesavec :- en exposant : attributs de groupement (
GROUP BY) - en indice : critère de restriction (
HAVING) sur les groupements.
Cette écriture supposant qu’on élimine les doublons.
Arbre de requêtes :
Savoir appliquer, sous forme d’arbre, des fonctions d’agrégat (COUNT, SUM, MAX, MIN, AVG) sur les recherches « Aux pays des bières ».
-
Sur une requête simple
Construire un arbre de requêtes répondant à la question :
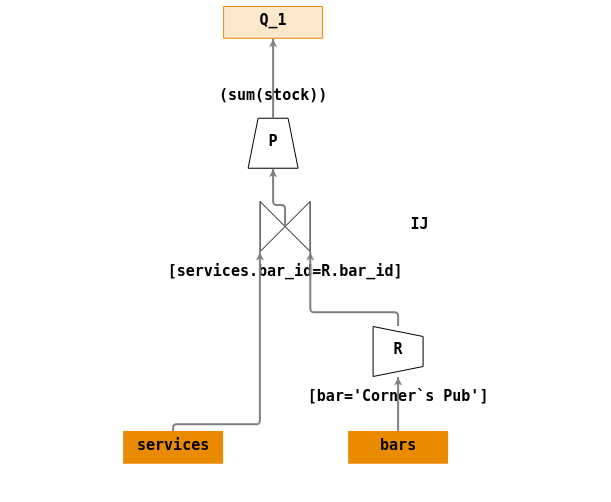
- \(Q_1\) : « Quelle est la quantité de bières en stock au “Corners Pub” ? ».
Votre réponse :
Arbre de requêtes : graph75.jsonTables
Opérateurs unaires
Opérateurs binaires
Vue d'ensemble Une solution possible :
Ecriture en algèbre relationnelle :
- \(R = \sigma_{[bar='Corner`s \; Pub]}(bars)\)
- \(IJ = \Join_{[R.bar\_id=services.bar\_id]}(R,services)\)
- \(P = \Pi_{(sum(stock))}(IJ)\)
- \(Q_1 = P\)
Arbre de requêtes :
-
Sur une requête imbriquée (1/2)
Construire un arbre de requêtes répondant à la question :
- \(Q_1\) : « Rechercher le nom des bières servies au “Bar du Coin” en quantité supérieure à la moyenne de tous les stocks ».
Votre réponse :
Arbre de requêtes : graph79.jsonTables
Opérateurs unaires
Opérateurs binaires
Vue d'ensemble biere Kronenbourg Une solution possible :
- Ecriture en algèbre relationnelle :
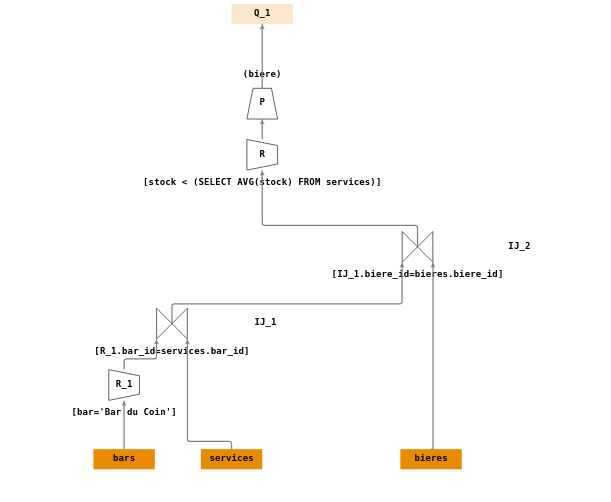
- \(R_1 = \sigma_{[bar='Bar \; du \; Coin']}(bars)\)
- \(IJ_1 = \Join_{[R_1.bar\_id=services.bar\_id]}(R_1,services)\)
- \(IJ_2 = \Join_{[IJ_1.biere\_id=bieres.biere\_id]}(IJ_1,bieres)\)
- \(average=\Pi_{(avg(stock))]}(services)\)
- \(R_2 = \sigma_{[stock < average]}(IJ_2)\)
- \(P = \Pi_{(biere)}(R_2)\)
- \(Q_1 = P\)
Arbre de requêtes :
-
Sur une requête imbriquée (2/2)
Construire un arbre de requêtes répondant à la question :
- \(Q_1\) : « Rechercher le nom des bars servant de la “Spaten” en quantité supérieure au maximum des stocks de bières du “Bar du Coin” ».
Votre réponse :
Arbre de requêtes : graph84.jsonTables
Opérateurs unaires
Opérateurs binaires
Vue d'ensemble Une solution possible :
Ecriture en algèbre relationnelle :
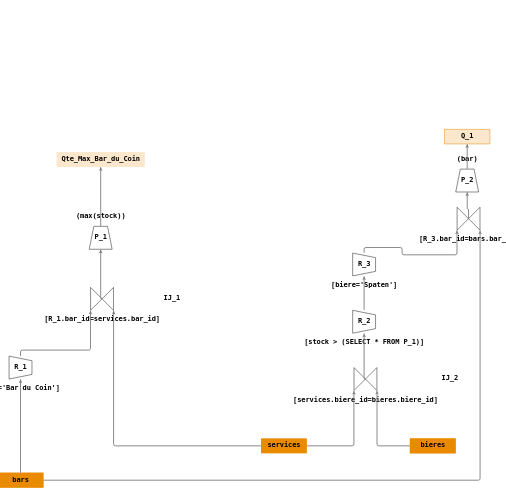
- \(R_1 = \sigma_{[bar='Bar \; du \; Coin']}(bars)\)
- \(IJ_1 = \Join_{[R_1.bar\_id=services.bar\_id]}(bars,services)\)
- \(max\_bdc=\Pi_{(max(stock))}(IJ_1)\)
- \(IJ_2 = \Join_{[services.biere\_id=bieres.biere\_id]}(services,bieres)\)
- \(R_2 = \sigma_{[biere='Spaten']}(IJ_2)\)
- \(R_3 = \sigma_{[stock > max\_bdc]}(R_2)\)
- \(IJ_3 = \Join_{[R_3.bar\_id=bars.bar\_id]}(R_3,bars)\)
- \(P = \Pi_{(bar)}(R_3)\)
- \(Q_1 = P\)
Arbre de requêtes :
Savoir regrouper, sous forme d’arbre, (GROUP BY) les informations, définir des conditions sur les regroupements (HAVING)
et appliquer des fonctions d’agrégat sur ces regroupements.
-
GROUP BY
Construire un arbre de requêtes répondant à la question :
- \(Q_1\) : « Rechercher le nom, la couleur des bières et leur quantité en stock dans la base de données ».
Votre réponse :
Arbre de requêtes : graph89.jsonTables
Opérateurs unaires
Opérateurs binaires
Vue d'ensemble Une solution possible :
Ecriture en algèbre relationnelle :
- \(IJ = \Join_{[services.biere\_id=bieres.biere\_id]}(services,bieres)\).
- \(G = G_{[]}^{(biere,couleur)}(NJ)\).
- \(Q_1 = \Pi_{(biere,couleur,sum(stock))}(G)\).
Arbre de requêtes :
-
GROUP BY HAVING
Construire un arbre de requêtes répondant à la question :
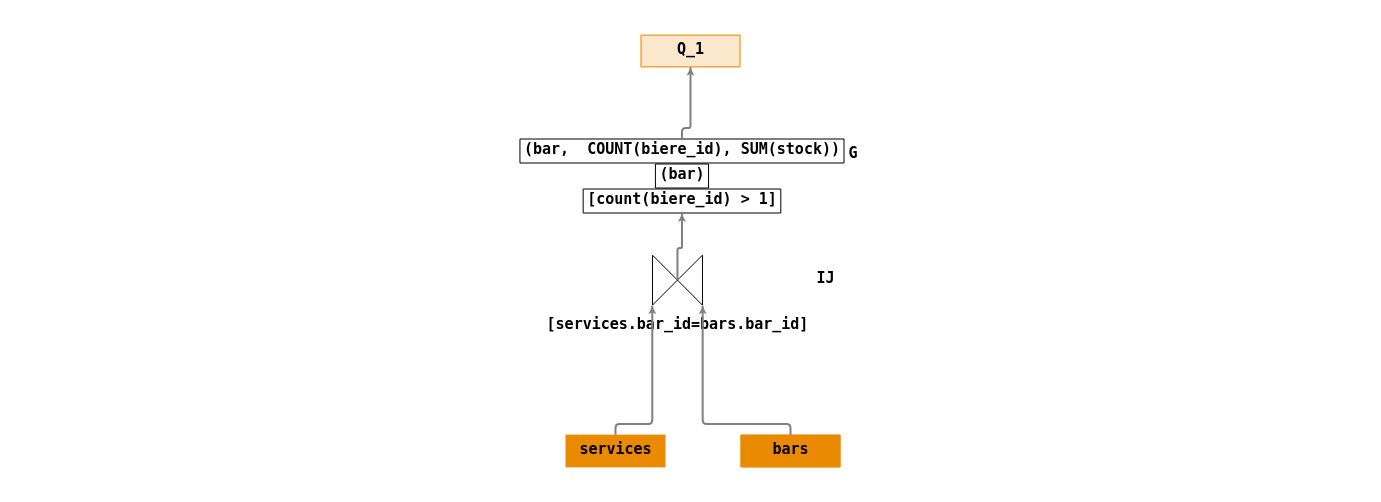
- \(Q_1\) : « Rechercher le nom des bars, le nombre de bières qu’ils servent et la somme de leur stocks pour les bars qui servent au moins deux bières ».
Votre réponse :
Arbre de requêtes : graph93.jsonTables
Opérateurs unaires
Opérateurs binaires
Vue d'ensemble Une solution possible :
Ecriture en algèbre relationnelle :
- \(IJ = \Join_{[services.bar\_id=bars.bar\_id]}(services,bars)\).
- \(G = G_{[count(biere\_id) > 1]}^{(bar)}(IJ)\).
- \(Q_1 = \Pi_{(bar,count(biere\_id),sum(stock))}(G)\).
Arbre de requêtes :
-
GROUP BY HAVING, requête imbriquée
Construire un arbre de requêtes répondant à la question :
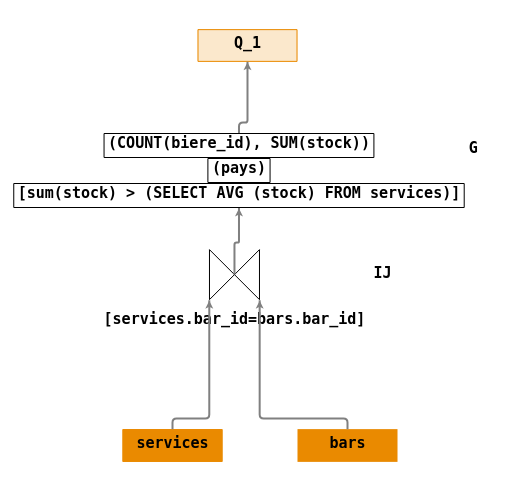
- \(Q_1\) : « Rechercher le nom des pays, le nombre de toutes les bières servies dans ces pays et la somme de leurs stocks, pour les pays dont la quantité de bières est supérieure à la moyenne des stocks mondiaux ».
Votre réponse :
Arbre de requêtes : graph97.jsonTables
Opérateurs unaires
Opérateurs binaires
Vue d'ensemble Une solution possible :
Ecriture en algèbre relationnelle :
- \(IJ = \Join_{[services.bar\_id=bars.bar\_id]}(services,bars)\).
- \(average=\Pi_{(avg(stock))]}(services)\)
- \(G = G_{[sum(stock)> average]}^{(pays)}(IJ)\).
- \(Q_1 = \Pi_{(pays,count(biere\_id),sum(stock))}(G)\).
Arbre de requêtes :
-
WHERE, GROUP BY HAVING
Construire un arbre de requêtes répondant à la question :
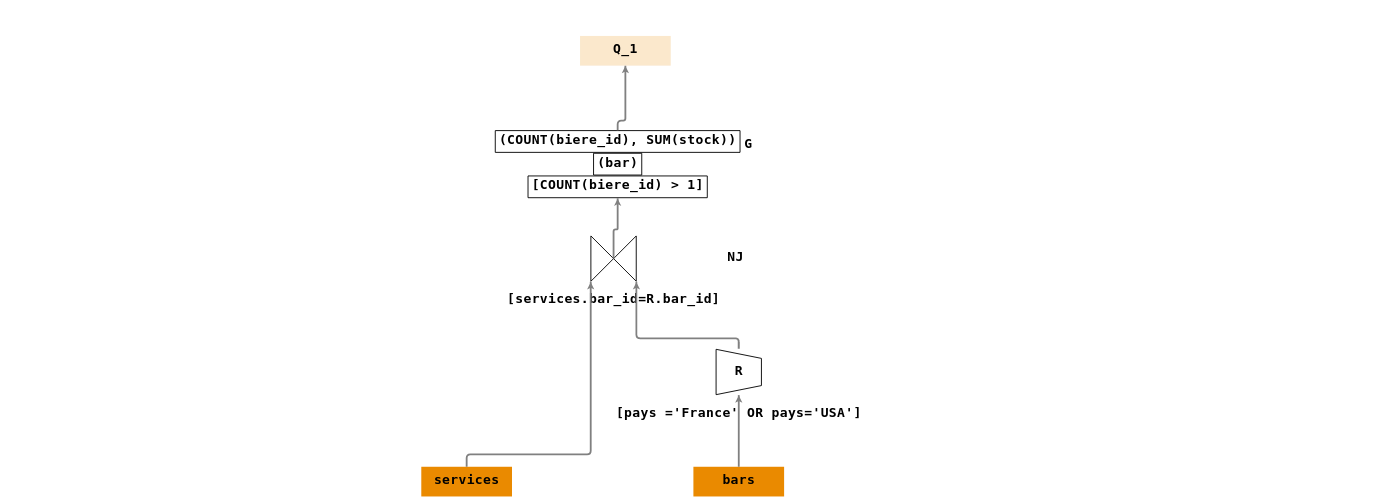
- \(Q_1\) : « Rechercher le nom des bars, le nombre de toutes les bières servies dans ces bars et la somme de leurs stocks, pour les bars de “France” ou des “USA” servant plus d’une bière ».
Votre réponse :
Arbre de requêtes : graph101.jsonTables
Opérateurs unaires
Opérateurs binaires
Vue d'ensemble Une solution possible :
Ecriture en algèbre relationnelle :
- \(R = \sigma_{[pays ='France' \; \lor \; pays='USA']}(bars)\)
- \(IJ = \Join_{[services.bar\_id=R.bar\_id]}(services,R)\)
- \(G = G_{[count(biere\_id) > 1)]}^{(bar)}(IJ)\).
- \(Q_1 = \Pi_{(bar,count(biere\_id),sum(stock))}(G)\).
Requêtes SQL
L’objectif des ces exercices est de savoir formuler des requêtes SQL sous la forme :
SELECT ... FROM ... WHERE ... GROUP BY ... HAVING ...
pour savoir rechercher les informations à partir :
- d’une seule table (projection et restriction)
- de plusieurs tables (jointures)
- des opérations ensemblistes (union,intersection,différence)
- de formulation de division relationnelle
- des fonctions d’agrégats
- des regroupements dans un ensemble avec restriction sur les groupements
Savoir formuler les requêtes sur une table en appliquant des :
- projections (\(\Pi\))
- restrictions (\(\sigma\))
en écrivant des expressions logiques dans les clauses de restriction.
-
Projection
Ecrire une requête SQL répondant à la question :
- \(Q_1\) : « Rechercher le nom et la couleur des bières ».
Votre réponse :
sql : bars.sqlOutputUne solution possible :
Ecriture en algèbre relationnelle :
- \(Q_1 = \Pi_{(biere,couleur)}(bieres)\)
On applique une projection (\(\Pi\)) sur les colonnes
(biere,couleur)de la tablebieres.Ecriture en langage SQL :
SELECT biere,couleur FROM bieres;
-
Restriction
Ecrire une requête SQL répondant à la question :
- \(Q_1\) : « Rechercher les bières d’origine française ».
Votre réponse :
sql : bars.sqlOutputUne solution possible :
Ecriture en algèbre relationnelle :
- \(Q_1 = \sigma_{[origine='France']}(bieres)\)
On applique une restriction (\(\sigma\)) sur la table
bieresavec la condition[origine='France'].Ecriture en langage SQL :
SELECT * FROM bieres WHERE origine='France';
-
Projection et Restriction
Ecrire une requête SQL répondant à la question :
- \(Q_1\) : « Rechercher le nom des bières françaises ».
Votre réponse :
sql : bars.sqlOutputUne solution possible :
Ecriture en algèbre relationnelle :
- \(Q_1 = \Pi_{(biere)}(\sigma_{[origine='France']}(bieres))\).
On applique une projection (\(\Pi\)) sur la colonne
biereet une restriction (\(\sigma\)) sur la condition[origine='France']de la tablebieres.Ecriture en langage SQL :
SELECT biere FROM bieres WHERE origine='France';
-
Connecteur logique
Ecrire une requête SQL répondant à la question :
- \(Q_1\) : « Rechercher les bières blondes françaises ».
Votre réponse :
sql : bars.sqlOutputUne solution possible :
Ecriture en algèbre relationnelle :
- \(Q_1 = \sigma_{[origine='France' \land couleur='Blonde']}(bieres)\).
On vérifie (\(\sigma\)) que les bières sont d’origine française (
origine='France') et (\(\land\)) qu’elles sont de couleur blonde (couleur='Blonde')Ecriture en langage SQL :
SELECT * FROM bieres WHERE origine='France' AND couleur='Blonde';
-
connecteurs logiques
Ecrire une requête SQL répondant à la question :
- \(Q_1\) : « Rechercher le nom et la couleur des bières françaises blondes et les bières brunes ».
Votre réponse :
sql : bars.sqlOutputUne solution possible :
Ecriture en algèbre relationnelle :
- \(Q_1 = \Pi_{(biere,couleur)}(\sigma_{[origine='France' \land couleur='Blonde' \lor couleur='Brune']}(bieres))\)
On vérifie (\(\sigma\)) sur la table
bieresqu’elles sont d’origine française et (\(\land\) : et logique) de couleur blonde ou (\(\lor\): ou logique) que la couleur des bières est brune.Ecriture en langage SQL :
SELECT biere,couleur FROM bieres WHERE origine='France' AND couleur='Blonde' OR couleur='Brune';
Attention à la priorité du connecteur logique \(\land\) sur le \(\lor\) (de même que la multiplication l’est sur l’addition).
- La requête :
- \(Q_1 = \sigma_{[origine='France' \lor couleur='Blonde' \land couleur='Brune']}(bieres)\)
donnerait comme résultat … les bières françaises (il ne peut exister des bières blonde et brune à la fois).
- Remarque : on peut modifier la priorité en parenthésant des parties de la restriction :
- \(Q_1 = \sigma_{[origine='France' \land (couleur='Blonde' \lor couleur='Brune')]}(bieres)\)
donnera comme résultat les bières françaises et les bières de couleur blonde ou brune.
Savoir formuler une requête sur plusieurs tables en faisant:
- produits cartésiens (\(\times\))
- jointures (\(\Join\))
Sachant qu’une jointure est une combinaison de produit cartésien (\(\times\)) et de restriction (\(\sigma\))
Savoir créer des vues qui contiennent les informations « métier » sur le modèle de données « Aux pays des bières ».
-
Produit cartésien et restriction
Ecrire une requête SQL répondant à la question :
- \(Q_1\) : « Rechercher les bars qui servent de la bière ».
Votre réponse :
sql : bars.sqlOutputUne solution possible :
Ecriture en algèbre relationnelle :
- \(IJ_1 = \Join_{[bars.bar\_id=services.bar\_id]}(bars,services)\)
- \(IJ_2 = \Join_{[IJ_1.biere\_id=bieres.biere\_id]}(IJ_1,bieres)\)
- \(Q_1 = IJ_2\)
On réalise ici deux jointures (\(\Join\)) entre les tables
bars,servicespuis une jointure entre le résultat obtenu (\(IJ_1\)) et la tablebieres.L’ordre d’éxecution des jointures (\(IJ_1\) avant ou après \(IJ_2\)) dépendra de l’état de la base de données (nombre d’enregistrements dans les tables, utilisation d’index sur colonnes …) et sera déterminé par l’optimiseur de requêtes du SGBD Relationnel utilisé.
Remarque :
une jointure est une combinaison de produit cartésien et de restriction, on peut les représenter à l’aide de ces opérateurs :
- \(IJ_1 = \sigma_{[bars.bar\_id=services.bar\_id]}(\times(bars,services))\)
- \(IJ_2 = \sigma_{[IJ_1.biere\_id=bieres.biere\_id]}(\times(IJ_1,bieres))\)
Ecriture en langage SQL :
SELECT * FROM bars, services s, bieres WHERE bars.bar_id = services.bar_id AND services.biere_id=bieres.biere_id;
On réalise, dans cette requête SQL, un produit cartésien (\(\times\)) entre les tables
bars,services,bierespuis on applique une restriction (\(\sigma\)) pour vérifier que chaque bar de l’ensemble desbarsest bien lié auxbieresqu’il sert par l’ensemble desservices:\([bars.bar\_id = services.bar\_id \land services.biere\_id=bieres.biere\_id]\)
Le produit cartésien (
CROSS JOIN) suivi d’une restriction (WHERE) peut aussi être mis en oeuvre en utilisant l’opérateur de jointure interne (INNER JOIN) avec une condition (ON) sur les colonnes de jointure.SELECT "" AS "Jointure interne"; SELECT * FROM bars INNER JOIN services INNER JOIN bieres ON (bars.bar_id=services.bar_id AND services.biere_id=bieres.biere_id);
Les colonnes de jointures ayant même nom (
bar\_id,biere\_id) et étant définies sur les même domaines (integer) nous pourrions aussi formuler cette requête par une jointure naturelle (\(\Join_{[]}\))SELECT * FROM bars NATURAL JOIN services NATURAL JOIN bieres;
Cependant les jointures naturelles sont à manipuler avec précaution. Il faut être sûr qu’il n’existe pas d’autres colonnes dans les tables qui pourraient être utilisés « naturellement » sans que nous le sachions.
-
Création de vue
Créer une vue barsdumonde sur les informations “métier” (sans les clés
bar_id,biere_id) des « bars qui servent de la bière ».Votre réponse :
sql : bars.sqlOutputUne solution possible :
Ecriture en algèbre relationnelle :
- \(IJ_1 = \Join_{[bars.bar_id=services.bar_id]}(bars,services)\)
- \(IJ_2 = \Join_{[NJ_1.biere_id=bieres.biere_id]}(IJ_1,bieres)\)
- \(barsdumonde = \Pi_{(bar,pays,stock,biere,couleur,origine)}(IJ_2)\)
Ecriture en langage SQL :
CREATE VIEW barsdumonde AS SELECT bar,pays,continent,biere,couleur,origine,stock FROM bars, services, bieres WHERE bars.bar_id = services.bar_id AND services.biere_id=bieres.biere_id; SELECT "" AS "Informations sur les Bars du Monde"; SELECT * FROM barsdumonde;
On “encapsule” dans une vue (
CREATE VIEW barsdumonde AS) une requête SQL pour consulter plus simplement les informations “métier” (sans les clés primaires et étrangères). (bar,pays,stock,biere,couleur,origine).
Savoir formuler des opérations ensemblistes (\(\cup,\cap,\setminus\)) sur le modèle de données « Aux pays des bières ».
- Union (\(\cup\))
- Intersection (\(\cap\))
- Différence (\(\setminus\))
-
Union
Ecrire une requête SQL répondant à la question :
- \(Q_1\) : « récupérer les noms des pays ou se trouvent des bars et ceux des origines de fabrication des bières ».
Votre réponse :
sql : bars.sqlOutputUne solution possible :
Ecriture en algèbre relationnelle :
- \(P_1 = \Pi_{(pays)}(bars)\)
- \(P_2 = \Pi_{(origine)}(bieres)\)
- \(U_1 = \cup(P_1,P_2)\)
Ecriture en langage SQL :
SELECT pays FROM bars UNION SELECT origine FROM bieres;
On applique d’abord une projection (\(\Pi\)) sur les colonnes
paysde tablebarsetoriginede la tablebierespour pouvoir mettre en oeuvre l’opération ensembliste d’union (\(\cup\)).Les opérations ensemblistes sont des opérateurs binaires qui doivent avoir pour chaque entrée (opérande) le même nombre d’attributs, chacun étant défini sur le même domaine.
Pour obtenir d’abord le nom des pays où se trouvent les bars suivi de celui d’origine de fabrication des bières on pourra faire en SQL un
UNION ALLqui concatène le résultat des deux requêtes.SELECT pays FROM bars UNION ALL SELECT origine FROM bieres;
Pour éliminer les doublons dans les deux requêtes concaténées on peut appliquer un distinct sur chcune des requêtes
SELECT DISTINCT pays FROM bars UNION ALL SELECT DISTINCT origine FROM bieres;
Il pourra cependant subsister des doublons dans le résultat final de la requête. Le résultat de cette requête ne sera donc pas nécessairement un ensemble.
-
Intersection
Ecrire une requête SQL répondant à la question
- \(Q_1\) : « Rechercher les noms des pays qui produisent de la bière et qui ont des bars ».
Votre réponse :
sql : bars.sqlOutputUne solution possible :
Ecriture en algèbre relationnelle :
- \(P_1 = \Pi_{(origine)}(bieres)\)
- \(P_2 = \Pi_{(pays)}(bars)\)
- \(I_1 = \cap(P_1,P_2)\)
Ecriture en langage SQL :
SELECT origine FROM bieres; INTERSECT SELECT pays FROM bars
On applique d’abord une projection (\(\Pi\)) sur les colonnes
originede tablebieresetpaysde la tablebarspour pouvoir appliquer l’opération ensembliste d’intersection (\(\cap\)).Les opérations ensemblistes sont des opérateurs binaires qui doivent avoir pour chaque entrée (opérande) le même nombre d’attributs, chacun étant défini sur le même domaine.
On pourra aussi formuler cette recherche par une requête imbriquée avec un
IN(\(\in\)).SELECT origine FROM bieres WHERE origine IN ( SELECT pays FROM bars );
Dans ce type de requête on parcourt tous les élementd de l’ensemble de la requête externe et on vérifie qu’il sont (appartiennent à) dans l’ensemble retourné par la requête imbriquée.
De même on pourra exprimer cette recherche par une requête imbriquée avec un
EXISTS(\(\exists\)). On vérifie la condition d’existence de chaque élément de la requête externe dans la requête imbriquée.SELECT origine FROM bieres WHERE EXISTS ( SELECT * FROM bars WHERE origine=pays );
Enfin, dans le cas de l’intersection, on peut tout aussi bien faire un produit cartésien et une restriction avec un test d’égalité entre le nom d’origine de fabrication des bières et celui des pays où se trouvent les bars.
SELECT origine FROM bieres, bars WHERE origine = pays;
-
Différence
- Ecrire une requête SQL répondant à la question
- \(Q_1\) : « Rechercher les noms des pays qui produisent de la bière et qui n’ont pas de bars ».
Votre réponse :
sql : bars.sqlOutputUne solution possible :
Ecriture en algèbre relationnelle :
- \(P_1 = \Pi_{(origine)}(bieres)\)
- \(P_2 = \Pi_{(pays)}(bars)\)
- \(E_1 = \setminus(P_1,P_2)\)
Ecriture en langage SQL :
SELECT origine FROM bieres EXCEPT SELECT pays FROM bars;
On applique d’abord une projection (\(\Pi\)) sur les colonnes
paysde tablebarsetoriginede la tablebierespour pouvoir appliquer l’opération ensembliste de différence (\(\displaystyle {\setminus}\)).Les opérations ensemblistes sont des opérateurs binaires qui doivent avoir pour chaque entrée (opérande) le même nombre d’attributs, chacun étant défini sur le même domaine.
Contrairement aux opérations ensemblistes d’union et d’intersection, la différence n’est pas commutative.
On pourra aussi formuler cette recherche par une requête imbriquée avec un
NOT IN(\(\notin\)).SELECT origine FROM bieres WHERE origine IN ( SELECT pays FROM bars );
Dans ce type de requête on parcourt tous les élements de l’ensemble de la requête externe et on vérifie qu’il ne sont pas (n’appartiennent pas à) dans l’ensemble retournée par la requête imbriquée.
De même on pourra exprimer cette recherche par une requête imbriquée avec un
NOT EXISTS(\(\nexists\)). On vérifie la condition de non-existence de chaque élément de la requête externe dans la requête imbriquée.SELECT origine FROM bieres WHERE EXISTS ( SELECT * FROM bars WHERE origine=pays );
Contrairement à l’opération d’intersection on ne pourra pas faire un produit cartésien et une restriction avec un test de non-égalité (différence) entre le nom des pays où se trouvent des bars et celui de l’origine de fabrication des bières.
SELECT origine FROM bieres, bars WHERE origine <> pays;
Cette requête ne donnerait pas les éléments recherchés mais tous les éléments issus du produit cartésien qui vérifient que l’origine de fabrication est différente du nom des pays où se trouvent les bars… on obtiendrait donc toutes les origine de fabrications des bières puisque toutes les combinaisons possibles ont été générés par le produit cartésien.
Savoir répondre « Aux pays des bières » à des questions du type :
- “trouve-moi les \(x\) qui sont associés à tous (\(\forall\)) les \(y\)“
Dans notres cas, par exemple :
- “trouver les bars qui servent toutes les bières
-
DOUBLE NEGATION (1/2)
Ecrire une requête SQL répondant à la question \(Q_1\) :
- \(Q_1\) : « quels sont les identifiants des bars qui servent toutes les bières ? ».
Votre réponse :
sql : bars.sqlOutputUne solution possible :
Ecriture en algèbre relationnelle :
- \(P_1 = \Pi_{(bar\_id,biere\_id)}(services)\)
- \(P_2 = \Pi_{(biere\_id)}(bieres)\)
- \(D = \div(P_1,P_2)\)
L’opération de division relationnelle n’existe pas en SQL, mais on peut le mettre en œuvre à l’aide d’une double négation (
NOT EXISTSimbriqués).- On reformulerait la question :
- « trouver les identifiants des bars tel qu’il n’existe pas de bières pour lesquelles il n’existe pas de service associant le bar en question avec cette bière ».
Ecriture en langage SQL :
SELECT DISTINCT bar_id FROM services s1 WHERE NOT EXISTS ( SELECT * FROM bieres bi WHERE NOT EXISTS ( SELECT * FROM services s2 WHERE s1.bar_id = s2.bar_id AND s2.biere_id = bi.biere_id ) );
De manière générique on peut formuler la division relationnelle pour récupérer dans l’ensemble
S(S[X,Y]) les éléments qui sont liés à tous ceux de l’ensembleT(T[Y]) par l’information (Y) par l’écriture de l’expression algèbrique :- \(\div(\Pi_{(X,Y)}(S),\Pi_{(Y)}(T))\)
que l’on peut traduire en SQL par :
SELECT se.X FROM S s1 WHERE NOT EXISTS ( SELECT * FROM T WHERE NOT EXISTS ( SELECT * FROM S s2 WHERE s1.X = s2.X AND s2.Y = T.Y ) );
-
DOUBLE NEGATION (2/2)
Ecrire une requête SQL répondant à la question \(Q_1\) :
- \(Q_1\) : « quels sont les noms des bars qui servent toutes les bières ? ».
Votre réponse :
sql : bars.sqlOutputUne solution possible :
Ecriture en algèbre relationnelle :
- \(P_1 = \Pi_{(bar\_id,biere\_id)}(services)\)
- \(P_2 = \Pi_{(biere\_id)}(bieres)\)
- \(D = \div(P_1,P_2)\)
- \(IJ_1 = \Join_{[D.bar\_id=bars.bar\_id]}(D,bars)\)
- \(P_3 = \Pi_{(bar)}(IJ_1)\)
On pourra met en œuvre l’opération de division relationnelle en reformulant la question :
- trouver le nom des bars tel qu’il n’existe pas de bières pour lesquelles il n’existe pas de service associant le bar en question à cette bière.
Ecriture en langage SQL :
SELECT bar FROM bars ba WHERE NOT EXISTS ( SELECT * FROM bieres bi WHERE NOT EXISTS ( SELECT * FROM services s WHERE ba.bar_id = s.bar_id AND s.biere_id = bi.biere_id ) );
La jointure interne (\(IJ_1\)) se faisant dans la requête la plus imbriquée.
On pourra aussi formuler cette requête par l’utilisation d’une opération ensembliste de différence :
SELECT bar FROM bars ba WHERE NOT EXISTS ( SELECT biere_id FROM bieres EXCEPT SELECT biere_id FROM services WHERE bar_id = ba.bar_id );
Cette formulation est très proche de la précédente, la comparaison sur les identifiants de bières se faisant sur les éléments récupérés par les deux requêtes mises en jeu dans l’opération ensembliste.
-
GROUP BY, COUNT (1/3)
Ecrire une requête SQL répondant à la question \(Q_1\) :
- \(Q_1\) : « quels sont les identifiants des bars qui servent toutes les bières ? ».
Votre réponse :
sql : bars.sqlOutputUne solution possible :
Ecriture en algèbre relationnelle :
- \(P_1 = \Pi_{(bar\_id,biere\_id)}(services)\)
- \(P_2 = \Pi_{(biere\_id)}(bieres)\)
- \(D = \div(P_1,P_2)\)
- \(Q_1 = \Pi_{(bar\_id)}(D)\).
L’opération de division relationnelle n’existe pas en SQL, mais on peut le mettre en œuvre en appliquant des fonctions d’agrégats sur des regroupements.
- En effet on peut compter le nombre de bières différentes servies par bar (
GROUP BY) et ne retenir (conditionHAVING) que ceux pour lesquels le nombre de bières est égal au nombre total de bières existantes dans la base de données. On peut donc reformuler la question : - trouver les identifiants des bars qui servent un nombre de bières différentes qui soit égal au nombre total de bières de la base de données.
Dans ce cas, on peut reformuler la division relationnelle par l’expression algébrique :
- \(nb\_bieres=\Pi_{count(biere\_id)}(bieres)\)
- \(G = G_{[count(biere\_id)=nb\_bieres]}^{(bar\_id)}(services)\).
- \(Q_1 = \Pi_{(bar\_id)}(G)\).
Le symbole \(G\) représente l’opérateur de regroupement appliqué sur la table
servicesavec :- en exposant : attributs de groupement (
GROUP BY) - en indice : critère de restriction (
HAVING) sur les groupements.
Cette écriture supposant qu’on élimine les doublons.
Ecriture en langage SQL :
SELECT DISTINCT bar_id FROM services s GROUP BY bar_id HAVING COUNT(DISTINCT biere_id) = (SELECT COUNT(biere_id) FROM bieres);
-
GROUP BY, COUNT (2/3)
Ecrire une requête SQL répondant à la question \(Q_1\) :
- \(Q_1\) : « quels sont les noms des bars qui servent toutes les bières ? ».
Votre réponse :
sql : bars.sqlOutputUne solution possible :
Ecriture en algèbre relationnelle :
- \(P_1 = \Pi_{(bar\_id,biere\_id)}(services)\)
- \(P_2 = \Pi_{(biere\_id)}(bieres)\)
- \(D = \div(P_1,P_2)\)
- \(IJ = \Join_{[D.bar\_id=bars.bar\_id]}(D,bars)\)
- \(P = \Pi_{(bar)}(IJ_1)\)
L’opération de division relationnelle n’existe pas en SQL, mais on peut le mettre en œuvre en appliquant des fonctions d’agrégats sur des regroupements.
- En effet on peut compter le nombre de bières différentes servies par bar (
GROUP BY) et ne retenir (conditionHAVING) que ceux pour lesquels le nombre de bières est égal au nombre total de bières existantes dans la base de données. On peut donc reformuler la question : - trouver les identifiants des bars qui servent un nombre de bières différentes qui soit égal au nombre total de bières de la base de données.
Dans ce cas, on peut reformuler la division relationnelle par l’expression algébrique :
- \(IJ = \Join_{[bars.bar\_id=services.bar\_id]}(bars,services)\)
- \(nb\_bieres=\Pi_{count(biere\_id)}(bieres)\)
- \(G = G_{[count(biere\_id)=nb\_bieres]}^{(bar)}(IJ_1)\).
- \(Q_1 = \Pi_{(bar)}(G)\).
Le symbole \(G\) représente l’opérateur de regroupement appliqué sur la table
servicesavec :- en exposant : attributs de groupement (
GROUP BY) - en indice : critère de restriction (
HAVING) sur les groupements.
Cette écriture supposant qu’on élimine les doublons.
Ecriture en langage SQL :
SELECT bar FROM bars INNER JOIN services ON (services.bar_id=bars.bar_id) GROUP BY bar HAVING COUNT(DISTINCT biere_id) = (SELECT COUNT(biere_id) FROM bieres);
-
GROUP BY, COUNT (3/3)
Ecrire une requête SQL répondant à la question \(Q_1\) :
- \(Q_1\) : « nom des bars qui servent toutes les bières et somme de leur stock de bières ».
Votre réponse :
sql : bars.sqlOutputUne solution possible :
Ecriture en algèbre relationnelle :
- \(P_1 = \Pi_{(bar\_id,biere\_id)}(services)\)
- \(P_2 = \Pi_{(biere\_id)}(bieres)\)
- \(D = \div(P_1,P_2)\)
- \(IJ = \Join_{[D.bar\_id=bars.bar\_id]}(D,bars)\)
- \(P = \Pi_{(bar,sum(stock))}(IJ_1)\)
L’opération de division relationnelle n’existe pas en SQL, mais on peut le mettre en œuvre en appliquant des fonctions d’agrégats sur des regroupements.
- En effet on peut compter le nombre de bières différentes servies par bar (
GROUP BY) et ne retenir (conditionHAVING) que ceux pour lesquels le nombre de bières est égal au nombre total de bières existantes dans la base de données. On peut donc reformuler la question : - trouver les identifiants des bars qui servent un nombre de bières différentes qui soit égal au nombre total de bières de la base de données.
Dans ce cas, on peut reformuler la division relationnelle par l’expression algébrique :
- \(IJ = \Join_{[bars.bar\_id=services.bar\_id]}(bars,services)\)
- \(nb\_bieres=\Pi_{count(biere\_id)}(bieres)\)
- \(G = G_{[count(biere\_id)=nb\_bieres]}^{(bar)}(IJ_1)\).
- \(Q_1 = \Pi_{(bar,sum(stock))}(G)\).
Le symbole \(G\) représente l’opérateur de regroupement appliqué sur la table
servicesavec :- en exposant : attributs de groupement (
GROUP BY) - en indice : critère de restriction (
HAVING) sur les groupements.
Cette écriture supposant qu’on élimine les doublons.
Ecriture en langage SQL :
SELECT bar,SUM(stock) FROM bars INNER JOIN services ON (services.bar_id=bars.bar_id) GROUP BY bars.bar_id,bar HAVING COUNT(DISTINCT biere_id) = (SELECT COUNT(biere_id) FROM bieres);
Remarque : on regroupe suivant les attributs (
bar_id,bar) car il peut arriver que deux bars aient le même nom mais soient différents.
Savoir appliquer des fonctions d’agrégat (COUNT, SUM, MAX, MIN, AVG) sur les recherches « Aux pays des bières ».
-
Sur une requête simple
Ecrire une requête SQL répondant à la question :
- \(Q_1\) : « Quelle est la quantité de bières en stock au “Corners Pub” ? ».
Votre réponse :
sql : bars.sqlOutputUne solution possible :
Ecriture en algèbre relationnelle :
- \(R = \sigma_{[bar='Corner`s \; Pub]}(bars)\)
- \(IJ = \Join_{[R.bar\_id=services.bar\_id]}(R,services)\)
- \(P = \Pi_{(sum(stock))}(IJ)\)
Ecriture en langage SQL :
SELECT "" AS "Produit cartésien, restriction"; SELECT SUM(s.stock) AS "stocks" FROM services s, bars b WHERE s.bar_id=b.bar_id AND b.bar='Corner`s Pub'; SELECT "" AS "INNER JOIN "; SELECT SUM(s.stock) AS "stocks" FROM services s INNER JOIN bars b ON (s.bar_id=b.bar_id) WHERE bar='Corners Pub'; SELECT "" AS "NATURAL JOIN"; SELECT SUM(stock) AS "stocks" FROM services NATURAL JOIN bars WHERE bar='Corner`s Pub';
-
Sur une requête imbriquée (1/2)
Ecrire une requête SQL répondant à la question :
- \(Q_1\) : « Rechercher le nom des bières servies au “Bar du Coin” en quantité inférieure à la moyenne de tous les stocks ».
Votre réponse :
sql : bars.sqlOutputUne solution possible :
Ecriture en algèbre relationnelle :
- \(R_1 = \sigma_{[bar='Bar \; du \; Coin']}(bars)\)
- \(IJ_1 = \Join_{[R_1.bar\_id=services.bar\_id]}(R_1,services)\)
- \(IJ_2 = \Join_{[IJ_1.biere\_id=bieres.biere\_id]}(IJ_1,bieres)\)
- \(average=\Pi_{(avg(stock))]}(services)\)
- \(R_2 = \sigma_{[stock < average]}(IJ_2)\)
- \(P = \Pi_{(biere)}(R_2)\)
Ecriture en langage SQL :
SELECT biere FROM bars, services,bieres WHERE bars.bar_id=services.bar_id AND services.biere_id=bieres.biere_id AND bar='Bar du Coin' AND stock < ( SELECT AVG(stock) FROM services );
-
Sur une requête imbriquée (2/2)
Ecrire une requête SQL répondant à la question
- \(Q_1\) : « Rechercher le nom des bars servant de la “Spaten” en quantité supérieure au maximum des stocks de bières du “Bar du Coin” ».
Votre réponse :
sql : bars.sqlOutputUne solution possible :
Ecriture en algèbre relationnelle :
- \(R_1 = \sigma_{[bar='Bar \; du \; Coin']}(bars)\)
- \(IJ_1 = \Join_{[R_1.bar\_id=services.bar\_id]}(bars,services)\)
- \(max\_bdc=\Pi_{(max(stock))}(IJ_1)\)
- \(IJ_2 = \Join_{[services.biere\_id=bieres.biere\_id]}(services,bieres)\)
- \(R_2 = \sigma_{[biere='Spaten']}(IJ_2)\)
- \(R_3 = \sigma_{[stock > max\_bdc]}(R_2)\)
- \(IJ_3 = \Join_{[R_3.bar\_id=bars.bar\_id]}(R_3,bars)\)
- \(P = \Pi_{(bar)}(R_3)\)
Ecriture en langage SQL :
SELECT bar FROM bars, services,bieres WHERE bars.bar_id=services.bar_id AND services.biere_id=bieres.biere_id AND biere='Spaten' AND stock > ( SELECT MAX(stock) FROM bars INNER JOIN services ON (bars.bar_id=services.bar_id) WHERE bar='Bar du Coin' );
Savoir regrouper (GROUP BY) les informations, définir des conditions sur les regroupements (HAVING)
et appliquer des fonctions d’agrégat sur ces regroupements.
-
Groupement
- Ecrire une requête SQL répondant à la question
- \(Q_1\) : « Rechercher le nom, la couleur des bières et leur quantité en stock dans la base de données ».
Votre réponse :
sql : bars.sqlOutputUne solution possible :
Ecriture en algèbre relationnelle :
- \(IJ = \Join_{[services.biere\_id=bieres.biere\_id]}(services,bieres)\).
- \(G = G_{[]}^{(biere,couleur)}(NJ)\).
- \(Q_1 = \Pi_{(biere,couleur,sum(stock))}(G)\).
Ecriture en langage SQL :
SELECT biere, couleur, SUM(stock) FROM services INNER JOIN bieres ON (services.biere_id=bieres.biere_id); GROUP BY biere, couleur;
On fait un regroupement (
GROUP BY) des bières qui sont servies par nom de bières (biere) et leurcouleurOn récupère dans le résultat final les attribut de groupement (code:nom,couleur) et on calcule sur ces regroupements la somme des quantités servies (code:SUM(stock)).
-
Groupement et restriction
Ecrire une requête SQL répondant à la question :
- \(Q_1\) : « Rechercher le nom des bars, le nombre de bières qu’ils servent et la somme de leur stocks pour les bars qui servent au moins deux bières ».
Votre réponse :
sql : bars.sqlOutputUne solution possible :
Ecriture en algèbre relationnelle :
- \(IJ = \Join_{[services.bar\_id=bars.bar\_id]}(services,bars)\).
- \(G = G_{[count(biere\_id) > 1]}^{(bar)}(IJ)\).
- \(Q_1 = \Pi_{(bar,count(biere\_id),sum(stock))}(G)\).
Ecriture en langage SQL :
SELECT bar, COUNT(biere_id), SUM(stock) FROM bars INNER JOIN services ON (bars.bar_id=services.bar_id); GROUP BY bar HAVING COUNT (biere_id) > 1;
On fait un regroupement (
GROUP BY) parbarservant des bières.On ne retient (
HAVING) dans ce regroupement que les bars qui servent au moins 2 bières différentes.On récupère dans le résultat final le nom des bars, leur nombre de bières et la quantité totale (
bar,COUNT(id_biere),SUM(stock)) servie dans ces bars. -
Groupement et restriction avec requête imbriquée
Ecrire une requête SQL répondant à la question
- \(Q_1\) : « Rechercher le nom des pays, le nombre de toutes les bières servies dans ces pays et la somme de leurs stocks, pour les pays dont la quantité de bières est supérieure à la moyenne des stocks mondiaux ».
Votre réponse :
sql : bars.sqlOutputUne solution possible :
Ecriture en algèbre relationnelle :
- \(IJ = \Join_{[services.bar\_id=bars.bar\_id]}(services,bars)\).
- \(average=\Pi_{(avg(stock))]}(services)\)
- \(G = G_{[sum(stock)> average]}^{(pays)}(IJ)\).
- \(Q_1 = \Pi_{(pays,count(biere\_id),sum(stock))}(G)\).
Ecriture en langage SQL :
SELECT pays, COUNT(biere_id), SUM(stock) FROM bars INNER JOIN services ON (bars.bar_id=services.bar_id); GROUP BY pays HAVING SUM(stock)> ( SELECT AVG( stock ) FROM services );
On fait un regroupement (
GROUP BY) par nom depaysdes bars servant des bières. On ne retient dans ces regroupements que lespaysdont la somme desstockde bières de leurs bars est supérieure à la moyenne des stocks mondiaux. On obtient dans le résultat final le nom des pays, le nombre de bières et la somme desstockservies dans cespays. -
Restriction, groupement et restriction
Ecrire une requête SQL répondant à la question
- \(Q_1\) : « Rechercher le nom des bars, le nombre de toutes les bières servies dans ces bars et la somme de leurs stocks, pour les bars de “France” ou des “USA” servant plus d’une bière ».
Votre réponse :
sql : bars.sqlOutputUne solution possible :
Ecriture en algèbre relationnelle :
- \(R = \sigma_{[pays ='France' \; \lor \; pays='USA']}(bars)\)
- \(IJ = \Join_{[services.bar\_id=R.bar\_id]}(services,R)\)
- \(G = G_{[count(biere\_id) > 1)]}^{(bar)}(IJ)\).
- \(Q_1 = \Pi_{(bar,count(biere\_id),sum(stock))}(G)\).
Ecriture en langage SQL :
SELECT bar, COUNT( biere_id),SUM(stock) FROM bars INNER JOIN services ON (bars.bar_id=services.bar_id); WHERE (pays ='France' OR pays='USA') GROUP BY bar HAVING COUNT (biere_id) > 1;
On récupère les services des bars des deux pays (
pays ='France' OR pays='USA'), puis on les regroupe par nom de bar (GROUP BY bar)On ne retient dans ces regroupements que les
bardont le nombre de bières qu’ils servent est supérieur à la moyenne des stocks mondiaux.On récupère dans le résultat final le nom des bars,le nombre de bières qu’ils servent et la somme des stocks de bières servies dans ces bars (
bar, COUNT( biere_id ),SUM(stock))