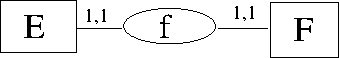Fichier de rejeu Close
Indication Close
A propos de... Close
Commentaire Close
Systèmes d'Information
- Notions mathématiques
- Calcul relationnel
- Algèbre relationnelle
- Langage de requêtes
- Arbre de requêtes
- Exercices
- Introduction
- Commandes de bases
- Langage de définition de données (LDD)
- Langage de manipulation de données (LMD)
- Types de données
- Exercice
- Dépendances fonctionnelles
- Décomposition de relations
- Inférence logique
- Normalisation
- Aux pays des bières
- Modélisation
- Exercices
© Your Copyright
Aide
Bijection
Nous présentons ici la définition d’une bijection entre deux ensembles sous forme de :
- définition mathématique
- cardinalité d’une relation bijective
- diagramme sagittal
- modèle Entité-Association
- modélisation UML
puis nous illustrons cette notion mathématique sur un exemple simple d’un ensemble d’employés et de sociétés.
Une relation binaire applicative, notée \(f\), est une bijection si et seulement si :
- \(\forall y \in F, \exists! x \in E, x=f(y)\)
Autrement dit, une application bijective \(f\) d’un ensemble \(E\) vers un ensemble \(F\) notée :
\[f : E \rightarrow F\]\[ x \mapsto f(x)\]est une application de \(E\) vers \(F\) pour laquelle :
- tout élément de l’ensemble d’arrivée possède un et un seul antécédent dans l’ensemble de départ et réciproquement.
ou encore :
- c’est une application injective et surjective.
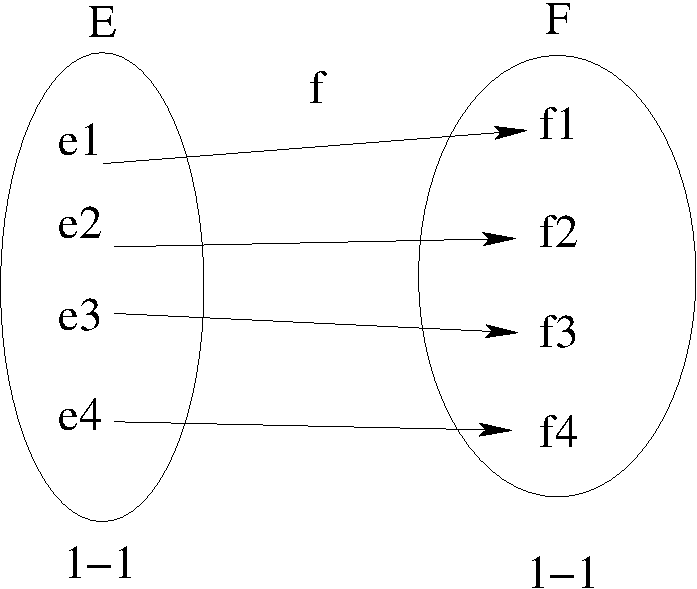
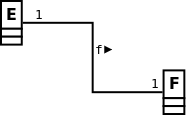
- \((1-1)\) : chaque élément de \(E\) est en relation avec un et un seul élément de \(F\).
- \((1-1)\) : chaque élément de \(F\) est en relation avec un et un seul élément de \(E\).
Le diagramme sagittal ci-dessous représente un exemple de relation applicative.
Les cardinalités de l’application bijective sont representées sous les ensembles \(E,F\).
La répresentation d’une application bijective dans un modèle Entité-Assocation se représente avec le formalisme ci-dessous :
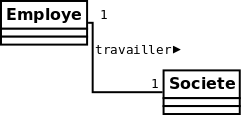
La répresentation d’une application bijective dans un modèle UML se représente avec le formalisme ci-dessous :
On veut modéliser un système d’information qui permettrait de gérer des employés dans des sociétés.
Dans cette application on veut exprimer la contrainte suivante sur les employés et les sociétés :
- tous les employés ont leur propre société et sont les seuls à y travailler.
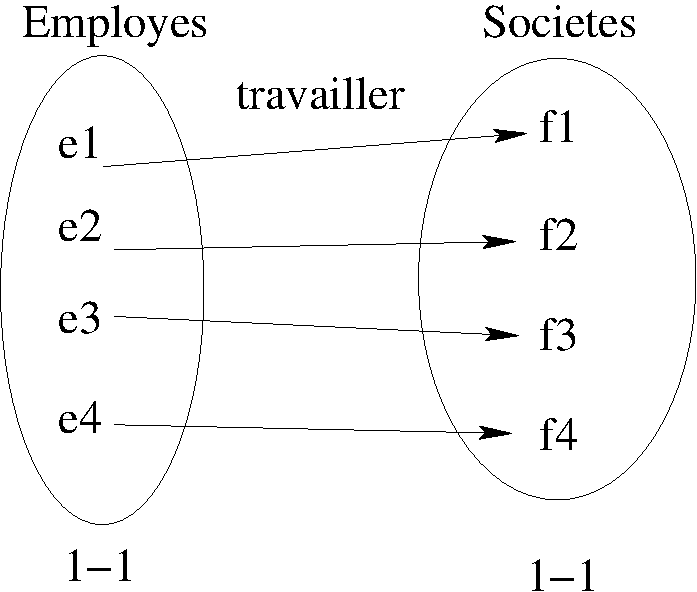
- \((1-1)\) : chaque
Employétravaille dans une seuleSociété. - \((1-1)\) : chaque
Sociétéa un seul \(Employé\).
Les contraintes de la relation Employé-Société sont celles d’une application bijective que l’on peut illustrer avec l’exemple de
diagramme sagittal ci-dessous :
La répresentation de l’application Employé-Société dans le formalisme Entité-Assocation :
La répresentation de l’application Employé-Société dans le formalisme UML :
