Fichier de rejeu Close
Indication Close
A propos de... Close
Commentaire Close
Systèmes d'Information
- Notions mathématiques
- Calcul relationnel
- Algèbre relationnelle
- Langage de requêtes
- Arbre de requêtes
- Exercices
- Introduction
- Commandes de bases
- Langage de définition de données (LDD)
- Langage de manipulation de données (LMD)
- Types de données
- Exercice
- Dépendances fonctionnelles
- Décomposition de relations
- Inférence logique
- Normalisation
- Aux pays des bières
- Modélisation
- Exercices

© Your Copyright
Aide
Notions mathématiques
Les Sytèmes d’Information reposant sur le modèle relationnel sont basés sur la manipulation d’ensembles de données et des relations que l’on peut établir entre ces ensembles. Historiquement, les chercheurs ont essayé de modéliser les langages d’interrogation de bases de données par la logique (Gardarin). Ainsi sont nés les calculs relationnels, véritables langages d’interrogation reposant sur la logique du premier ordre. D’un point de vue théorique, les approches par la logique permettent une meilleure compréhension des langages des SGBD, des mécanismes de raisonnements sous jacents et des techniques d’optimisation.
Pour toutes ces raisons il est donc nécessaire d’assimiler les concepts sur lesquels reposent les SGBD relationnels afin de pouvoir maîtriser la modélisation (structuration des données) et l’interrogation (écriture de requêtes) d’un système d’information relationnel.
Dans ce qui suit nous introduirons les concepts mathématiques en illustrant leur mise en application avec le langage de requêtes SQL (Structured Query Language) des Systèmes d’Information basés sur le modèle relationnel. Ce langage sera abordé plus en détail dans un prochain chapitre de ce cours.
Ensembles
Définition intuitive d’un ensemble
Un ensemble peut être vu comme :
- collection d’objets appelés éléments, sémantiquement définie mais non-structurée
- logique booléenne d'appartenance (\(\in\)) à un ensemble (\(E\)).
- l’élément, noté \(x\), est (\(x \in E\)) ou n’est pas (\(x \notin E\)) dans l’ensemble
- unicité : un élément n’est pas 2 fois dans le même ensemble
Ensemble vide
Représentation mathématique de l’ensemble vide :
- \(E = \{ \} = \emptyset\)
Création de l’ensemble vide en SQL :
On remarquera dans l’exécution du script ci-dessus les commandes SQL:
CREATE TABLE: de création deTABLEqui représentera un ensemble d’éléments (de données)SELECT: de recherche d’informations (d’éléments) dans une table (un ensemble)count(): de calcul sur les résultats d’une recherche d’informations
On remarquera également que la requête SQL :
SELECT x FROM E;
ne retourne aucun élément \(x\), l’exécution de cette requête sous SQLite ne produit aucun affichage entre les commentaires « ensemble vide » et « nombre d’éléments dans l’ensemble vide ».
Ensemble des chiffres arabes
Représentation mathématique de l’ensemble des chiffres arabes :
- \(E = \{ 0,1,2,3,4,5,6,7,8,9 \}\)
Création de l’ensemble des chiffres en SQL :
On remarquera dans l’exécution du script ci-dessus la commande SQL
INSERT INTO ... VALUES ...: d’insertion d’élément dans un ensemble
A partir de ces commandes SQL nous pouvons créer des ensembles dont les éléments peuvent contenir plusieurs informations.
Nous invitons le lecteur à faire l’exercice ci-dessous qui a pour objectif de créer un ensemble de points de coordonnées (x,y) avant de continuer la lecture de ce chapitre.
Créer un ensemble de points défini par les coordonnées (x,y) et insérer (INSERT INTO ... VALUES ...) dans cet ensemble les points définissant un carré de 100 unités de côté, centré en (0,0) dans un repère (Oxy).
Votre réponse :
Une solution possible :
CREATE TABLE points(x FLOAT,y FLOAT);
INSERT INTO points(x,y) VALUES (-50,-50);
INSERT INTO points(x,y) VALUES (50,-50);
INSERT INTO points(x,y) VALUES (50,50);
INSERT INTO points(x,y) VALUES (-50,50);
SELECT * from points;
Lors de l’exécution de ces requêtes SQL, on remarquera la représentation tabulaire du résultat sous forme de lignes et de colonne qui ne sera pas sans rappeler les tableurs type Excel. Les noms de colonnes (x,y) représentent les attributs (propriétés) de la table (entité). Les lignes représentent les informations (éléments,enregistrements,n-uplets) que l’on, insère dans la table.
Domaine d’un ensemble
On peut définir un domaine en extension (énumération des valeurs) :
- \(E= \{ 0,2,4,6,8 \}\) : ensemble des entiers naturels (\(\mathbb{N}\)) pairs inférieur à 10
Création de l’ensemble des chiffres pairs en SQL :
On peut définir, en calcul relationnel, un domaine en intension (compréhension), par une formule logique vérifiée par tous les éléments :
- \(E = \{ x \; \vert \; x \in \mathbb{N} \land x \equiv 0 \mod 2 \}\) : ensemble des entiers naturels (\(\mathbb{N}\)) pairs (congrus à 0 modulo 2)
ou de manière plus synthétique :
- \(E = \{ x \in \mathbb{N} \; \vert \; x \equiv 0 \mod 2 \}\) : ensemble des entiers naturels (\(\mathbb{N}\)) pairs
La première notation est cependant plus explicite sur la formulation en calcul relationnel, où l’on veut récupérer les éléments (\(x\)) qui vérifient la proposition logique :
- \(x \in \mathbb{N}\) : x appartient (« vrai ») ou n’appartient pas (« faux ») à l’ensemble des entiers
- \(\land\) : connecteur logique et (
ANDen SQL).- \(x \equiv 0 \mod 2\) : x est (« vrai ») ou n’est pas (« faux ») un nombre pair (congru à 0 modulo 2)
Si l’élément \(x\) est un entier et \(x\) est un nombre pair alors il appartient au domaine (\(x \in E\)) des entiers pairs défini par cette formule logique.
Le lecteur intéressé trouvera quelques notions supplémentaires sur la définition mathématique de la congruence en déployant le block ci-dessous.
Congruence de deux nombres (\(x,y\)) modulo \(n\) noté \(x \equiv y \; mod \; n\) :
- \((x-y)\) est un multiple de \(n\)
- \(n\) divise \((x-y)\)
Exemples : nombres pairs, impairs ?
- \(x \equiv 0 \; mod \; 2\) : (x-0) est un multiple de 2
- \(\Rightarrow\) (x-0)=2*k \(\Rightarrow\) x=2*k (x est pair CQFD).
- \(x \equiv 1 \; mod \; 2\) : (x-1) est un multiple de 2
- \(\Rightarrow\) (x-1)=2*k \(\Rightarrow\) x=2*k+1 (x est impair CQFD).
Exemple : savoir lire l’heure !
- \(x \equiv y \; mod \; 12\) : (x-y) est un multiple de 12.
- \(\Rightarrow\) (x-y)=12*k \(\Rightarrow\) x=12*k + y
- Autrement dit :
- \(12 \equiv 0 \; mod \; 12\) : midi ou minuit c’est pareil !
- \(14 \equiv 2 \; mod \; 12\) : 14 heures ou 2 heures de l’après-midi c’est pareil !
Pour en savoir un peu plus sur la congruence, nous invitons le lecteur à visionner la vidéo Micmath : multiplication proposé par Mickaël Launay
Fonction caractéristique
La fonction caractéristique (prédicat) d’un ensemble, notée \(P(x)\), définira en intension l’ensemble \(E\) :
- \(E = \{ x \; \vert \; P(x) \}\)
Exemple : définition de l’ensemble des entiers naturels impairs
- \(E = \{ x \mid x \in \mathbb{N} \land (x \equiv 1 \mod 2) \}\)
Fonction caractéristique \(P(x)\) :
- \(x \in \mathbb{N} \land (x \equiv 1 \mod 2)\)
Exemple : définition de l’ensemble des chiffres impairs
- \(E = \{ x \mid x \in \mathbb{N} \land (x \equiv 1 \mod 2) \land (x > 0 \land x <10) \}\)
Fonction caractéristique \(P(x)\) :
- \(x \in \mathbb{N} \land (x \equiv 1 \mod 2) \land (x > 0 \land x <10)\)
Fonction caractéristique en SQL:
En SQL, la fonction caractéristique est définie dans la clause WHERE par l’écriture d’une expression logique.
Votre réponse :
Représenter l’ensemble des chiffres pairs en intension et écrire la requête SQL correspondante.
Zone de saisie de texte
| Clavier | Action |
|---|---|
| F1 | Afficher une aide technique |
| F2 | Afficher une aide pédagogique |
| Ctrl-A | Tout sélectionner |
| Ctrl-C | Copier la sélection dans le presse-papier |
| Ctrl-V | Copier le presse-papier dans la sélection |
| Ctrl-X | Couper la sélection et la copier dans le presse-papier |
| Ctrl-Z | Annuler la modification |
| Maj-Ctrl-Z | Rétablir la modification |
| Menu | Action |
|---|---|
| Ré-initialiser les sorties | |
| Faire apparaître le menu d'aide | |
| Valider la zone de saisie | |
| Initialiser la zone de saisie | |
| Charger le contenu d'un fichier dans la zone de saisie | |
| Sauvegarder le contenu de la zone de saisie dans un fichier | |
| Imprimer le contenu de la zone de saisie |
Une solution possible :
Ensemble des chiffres pairs en intension :
- \(E = \{ x \; \mid \; x \in \mathbb{N} \land x \equiv 0 \mod 2 \land (x>=0 \land x<10) \}\)
Requête SQL pour récupérer les chiffres pairs dans l’ensemble des entiers :
SELECT x FROM E WHERE x%2 = 0 AND x >=0 AND x < 10;
On peut également créer des vues (CREATE VIEW) sur une partie (un sous-ensemble) d’un ensemble.
Dans le code SQL ci-dessous, nous récupérons l’ensemble des chiffres pairs ou impairs en créant des vues (E_even, E_odd), représentant ces deux sous-ensembles de l’ensemble \(\mathbb{N}\) des entiers, à l’aide des fonctions caractéristiques qui définissent logiquement les chiffres pairs ou impairs.
CREATE VIEW E_even AS
SELECT x AS "even digits"
FROM E
WHERE x%2 = 0 AND x >= 0 AND x < 9 ;
CREATE VIEW E_odd AS
SELECT x AS "odd digits"
FROM E
WHERE x%2 = 1 AND x > 0 AND x <= 9 ;
On peut alors utiliser ces vues (sous-ensembles) dans une requête comme on utilise une table (ensemble).
SELECT * FROM E_odd;
SELECT * FROM E_even;
Créer une vue revient à définir un sous-ensemble d’un ensemble, ce sous-ensemble étant représenté par une requête SQL.
Une vue revient à « encapsuler » une requête SQL en la nommant (un peu comme on encapsule du code dans une fonction en programmation).
Attention, il ne faut cependant pas confondre une table avec une vue.
Si nous avions créé des tables (E_even, E_odd) nous aurions alors dû insérer les chiffres pairs et impairs dans ces tables.
Nous aurions alors obtenu trois ensembles distincts (E,E_even, E_odd). L’insertion d’un entier pair dans l’ensemble (E) n’aurait pas été répercuté dans le sous-ensemble E_even. Reciproquement l’insertion d’un entier pair dans l’ensemble (E_even) n’aurait pas non plus été répercuté dans l’ensemble E.
Par contre si E_even est défini comme une vue sur les éléments pairs de l’ensemble E, l’insertion d’un entier pair dans cet ensemble sera « visible » lors d’une requête sur la vue (qui constitue elle-même une requête sur l’ensemble E).
Le code SQL ci-dessous représente la différence entre la création de tables et de vues pour représenter le sous-ensemble des chiffres impairs.
Dans le cas de création de table, l’insertion d’un nouvel élément dans l’ensemble des chiffres ne sera pas répercuté sur le sous-ensemble des chiffres impairs.
sql : essai.sqlOutput
On remarquera la commande de destruction d’une table (DROP TABLE).
Attention cette commande irréversible enlèvera de la base de données toute l’information contenue dans l’ensemble.
Cardinalité
La cardinalité d’un ensemble est le nombre d’éléments d’un ensemble, noté \(card(E)\).
En SQL on obtient la cardinalité d’un ensemble en appliquant la fonction de calcul \(count()\) sur l’ensemble généré par une requête.
Cardinalité d’un ensemble en SQL :
En utilisant les opérations ensemblistes d’union, d’intersection et de différence (\(\cup,\cap,\setminus\)), on pourra vérifier :
- \(card(E_1 \cup E_2) = card(E_1) + card(E_2) - card(E_1 \cap E_2)\)
- \(card(E_1 \setminus E_2) = card(E_1) - card(E_1 \cap E_2)\)
En SQL on pourra utiliser les opérations ensemblistes correspondantes (UNION,INTERSECT,EXCEPT) comme ilmlustré dans les exercices ci-dessous.
Votre réponse :
En utilisant les opérations ensemblistes d’union et d’intersection (\(\cup,\cap\)), vérifier à l’aide de requêtes SQL, l’expression suivante :
- \(card(E_1 \cup E_2) = card(E_1) + card(E_2) - card(E_1 \cap E_2)\)
lorsque \(E_1\) représente l’ensemble des chiffres pairs et \(E_2\) l’ensemble des chiffres impairs (\(E_2\))
Une solution possible :
- \(card(E_1 \cup E_2) = card(E_1) + card(E_2) - card(E_1 \cap E_2)\)
SELECT count(*) AS "card(E1 Union E2)"
FROM (SELECT * FROM E1 UNION SELECT * FROM E2);
SELECT "" AS "=";
SELECT count(*) AS "card(E1)" FROM E1;
SELECT "" AS "+";
SELECT count(*) AS "card(E2)" FROM E2;
SELECT "" AS "-";
SELECT count(*) AS "card(E1 Intersect E2)"
FROM (SELECT * FROM E1 INTERSECT SELECT * FROM E2);
Votre réponse :
En utilisant les opérations ensemblistes d’intersection et de différence (\(\cap,\setminus\)), vérifier à l’aide de requêtes SQL, l’expression suivante :
- \(card(E_1 \setminus E_2) = card(E_1) - card(E_1 \cap E_2)\)
lorsque \(E_1\) représente l’ensemble des chiffres arabes (\(E\)) et \(E_2\) l’ensemble des chiffres impairs (\(Digit\_odd\))
Une solution possible :
\(card(E_1 \setminus E_2) = card(E_1) - card(E_1 \cap E_2)\)
SELECT count(*) AS "card(E1 Minus E2)"
FROM (SELECT * FROM E1 EXCEPT SELECT * FROM E2);
SELECT "" AS "=";
SELECT count(*) AS "card(E1)" FROM E1;
SELECT "" AS "-";
SELECT count(*) AS "card(E1 Intersect E2)"
FROM (SELECT * FROM E1 INTERSECT SELECT * FROM E2);
Egalité d’ensembles
Deux ensembles \(A,B\) sont égaux, ce qu’on note \(A = B\), si tout élément de l’un appartient à l’autre et inversement.
Autrement dit l’ensemble \(A\) est inclus (\(\subseteq\)) dans l’ensemble \(B\) et réciproquement.
- \(A = B \Leftrightarrow A \subseteq B \land B \subseteq A\)
Dire qu’un ensemble \(A\) dans un ensemble \(E\) revient à vérifier :
- \(A \setminus E = 0\)
Autrement dit, si la différence entre l’ensemble \(A\) et l’ensemble \(E\) est vide alors tous les éléments de l’ensemble \(A\) sont dans l’ensemble \(E\).
L’inclusion d’un ensemble dans un autre peut également être définie par les fonctions caractéristiques d’ensemble.
Si \(P_A, P_E\) sont les fonctions caractéristiques des ensembles \(A,E\), alors \(A \subseteq E\) si et seulement si :
- \(\forall a \in A, P_A(a) \Rightarrow P_E(a)\)
Si le prédicat est vérifié pour les éléments du sous-ensemble \(A\) alors il est vérifié pour le prédicat de l’ensemble \(E\).
Exemples :
- un chiffre pair est un chiffre mais l’inverse n’est pas nécessairement vrai.
- l’humain est un mammifère mais tous les mammifères ne sont pas des humains.
- …
Vérification, en SQL, de l’inclusion d’un ensemble dans un autre et de l’égalité de deux ensembles :
On peut définir l’égalité de deux ensembles (\(A = B\)) par la propriété suivante :
- \(A \cup B = A \cap B\)
ou
- \((A \cup B) \setminus (A \cap B)= \emptyset\)
Votre réponse :
En utilisant les opérations ensemblistes d’union, d’intersection et de différence (\(\cup, \cap,\setminus\)), vérifier à l’aide de requêtes SQL, l’expression suivante :
- \((A \cup B) \setminus (A \cap B)= \emptyset\)
lorsque \(A\) représente l’ensemble des chiffres arabes dans l’ordre croissant et \(B\) l’ensemble des chiffres arabes dans l’ordre décroissant.
A partir de la table \(A\) on créera une vue pour représenter l’ensemble \(B\) en utilisant la table \(A\) dans une requête pour récupérer les éléments (chiffres arabes) dans l’ordre décroissant.
Une solution possible :
- \((A \cup B) \setminus (A \cap B)= \emptyset\)
CREATE VIEW B AS
SELECT * FROM A ORDER BY x DESC;
SELECT * FROM A;
SELECT * FROM B;
SELECT COUNT(*)
FROM
(
SELECT x FROM A UNION SELECT x FROM B
EXCEPT
SELECT x FROM A INTERSECT SELECT x FROM B
)
Parties d’un ensemble
L’ensemble \(A\) est un sous-ensemble, une partie, d’un ensemble \(E\) s’il est inclus dans \(E\) :
- \(\forall x \in A, x\in E\)
Autrement dit tous les éléments de l’ensemble \(A\) sont des éléments de l’ensemble \(E\).
Notation :
- \(A \subseteq E\) : l’ensemble \(A\) est inclus ou égal à l’ensemble \(E\)
- \(\mathscr{P}(E)\) : ensemble des sous-ensembles (ensemble des parties)
A partir de l’ensemble des entiers définis dans l’intervalle \(E=[-2,11]\), créer dans une vue (E_1) le sous-ensemble des chiffres pairs.
A partir de ces deux ensembles, récupérer dans une vue (E_2) le sous-ensemble des chiffres qui ne sont pas dans
le sous-ensemble des chiffres pairs (récupérer donc l’ensemble des chiffres impairs :) ).
Votre réponse :
Une solution possible :
SELECT * FROM E;
-- create view E1 (even digits) --
CREATE VIEW E1 AS
SELECT x FROM E WHERE x%2=0 AND x>=0 AND x<10;
SELECT x AS "even digits" FROM E1;
-- create view E2 (odd digits) --
CREATE VIEW E2 AS
SELECT x FROM E WHERE x>0 AND x<10 AND x NOT IN (SELECT x FROM E1);
SELECT x AS "odd digits" FROM E2;
-- card(E1\E) = 0 => E1 inclus dans E --
SELECT count(*) AS "card(E1\E)" FROM E1 EXCEPT SELECT x FROM E;
-- card(E\E1) --
SELECT count(*) AS "card(E\E1)" FROM E EXCEPT SELECT x FROM E1;
-- card(E2\E) = 0 => E2 inclus dans E ---
SELECT count(*) AS "card(E2\E)" FROM E2 EXCEPT SELECT x FROM E;
-- card(E\E2) --
SELECT count(*) AS "card(E\E2)" FROM E EXCEPT SELECT x FROM E2;
- A partir de l’ensemble des entiers (
E) de la base de données - créer dans des vues (
E1,E2) les sous-ensembles des chiffres pairs, impairs. - créer une vue (
E_numbers) sur l’ensemble des nombres qui ne sont pas des chiffres . - créer une vue (
E_Union) contituant l’union de ces trois parties.
- créer dans des vues (
Vérifier que l’ensemble des parties (E_Union) est bien égal à l’ensemble (E-E_Union=0).
Votre réponse :
Une solution possible :
SELECT * FROM E;
-- create view E1 : chiffres pairs --
CREATE VIEW E1 AS
SELECT x FROM E WHERE x%2=0 AND x>=0 AND x<10;
-- create view E2 : chiffres impairs --
CREATE VIEW E2 AS
SELECT x FROM E WHERE x>0 AND x<10 AND x NOT IN (SELECT x FROM E1);
SELECT x AS "even digits" FROM E1;
SELECT x AS "odd digits" FROM E2;
-- create view E_numbers --
CREATE VIEW E_numbers AS
SELECT x FROM E WHERE x NOT IN (SELECT x FROM E1) AND x NOT IN (SELECT x FROM E2);
SELECT x AS "numbers" FROM E_numbers;
-- create view E_union = E_numbers + E1 + E2 --
CREATE VIEW E_union AS
SELECT x FROM E_numbers
UNION
SELECT x FROM E1 UNION SELECT x FROM E2;
-- E - E_union = 0 --
SELECT count(*) AS "E-E_union=0" FROM (SELECT x FROM E EXCEPT SELECT x FROM E_union);
L’exercice proposé ci-dessous propose un récapitulatif des notions abordées précédemment sur les ensembles, cardinalité, sous-ensemble et partitions.
Cet exercice est extrait du site de Bertrand Liaudet dans son cours sur la « théorie des ensembles et bases de données ».
Enoncé : 200 élèves participent à une journée de sport. 3 sports sont au programme : le foot, la natation et la course à pieds. Chaque élève peut participer à 1, 2 ou 3 sports. Avec les informations ci-dessous, trouver le nombre d’élèves qui participent à un seul sport, à 2 sports et à trois sports :
- 10 élèves sont blessés et ne participent pas
- 18 participent au 3 sports
- 103 ne font que 2 sports
- 79 font du foot et de la natation
- 19 ne font que le la course
- 129 font de la natation dont 40 que de ça .
Indice :
Cet exercice pourra être résolu par une méthode de représentation d’ensembles sous forme de diagramme de Venn et de calcul de cardinalité d’ensembles.
Votre réponse :
Zone de saisie de texte
| Clavier | Action |
|---|---|
| F1 | Afficher une aide technique |
| F2 | Afficher une aide pédagogique |
| Ctrl-A | Tout sélectionner |
| Ctrl-C | Copier la sélection dans le presse-papier |
| Ctrl-V | Copier le presse-papier dans la sélection |
| Ctrl-X | Couper la sélection et la copier dans le presse-papier |
| Ctrl-Z | Annuler la modification |
| Maj-Ctrl-Z | Rétablir la modification |
| Menu | Action |
|---|---|
| Ré-initialiser les sorties | |
| Faire apparaître le menu d'aide | |
| Valider la zone de saisie | |
| Initialiser la zone de saisie | |
| Charger le contenu d'un fichier dans la zone de saisie | |
| Sauvegarder le contenu de la zone de saisie dans un fichier | |
| Imprimer le contenu de la zone de saisie |
Une solution possible :
Cet exercice pourra être résolu par une méthode de représentation d’ensembles sous forme de diagramme de Venn et de calcul de cardinalité d’ensembles.
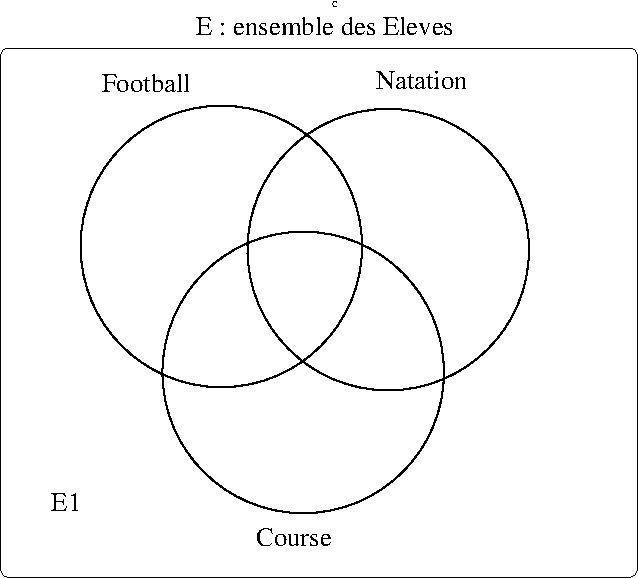
Ces ensembles représentent l’ensemble des élèves (\(E_1\)) qui ne feront pas de sports et les ensembles d’élèves qui font un ou plusieurs sports :
- \(E= E_1 \cup Football \cup Natation \cup Course\)
- où :
- \(card(E)=card(E_1)+card(Football)+card(Natation)+card(Course)=200\)
On défini alors un partitionnement de l’ensemble des élèves (\(E\)) en sous-ensembles :
- les élèves qui ne pourront participer à la journée de sport (\(E_1)\)
- les élèves qui participeront à un seul sport (\(E_2,E_3,E_4)\)
- les élèves qui participeront à deux sports (\(E_5,E_6,E_7)\)
- les élèves qui participeront aux trois sports(\(E_8)\)
représentés par le diagramme de Venn ci-dessous :
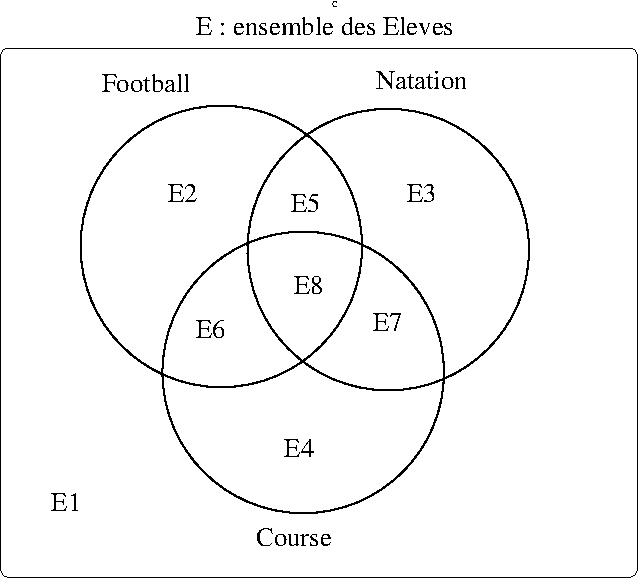
A partir des données du problème on peut déjà identifier :
10 élèves sont blessés et ne participent pas
\(\Rightarrow card(E_1)=10\)
18 participent au 3 sports
\(\Rightarrow card(E_8)=18\)
103 ne font que 2 sports
79 font du foot et de la natation
19 ne font que le la course
\(\Rightarrow card(E_4)=19\)
129 font de la natation dont 40 que de ça .
\(\Rightarrow card(E_3)=40\)
représentés par le diagramme de Venn ci-dessous :
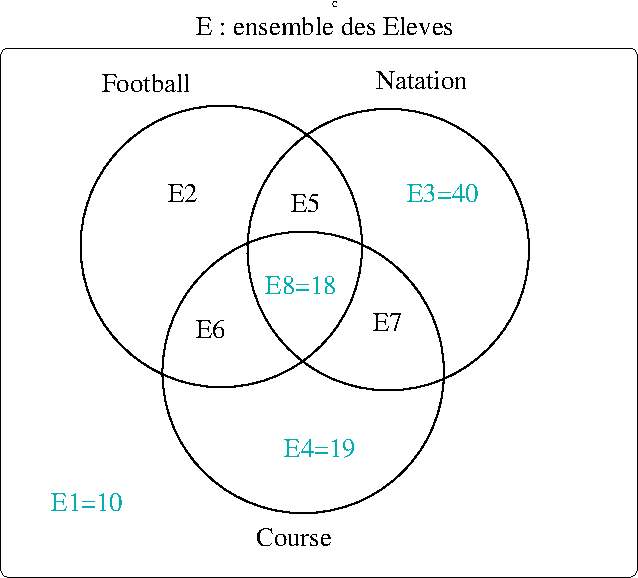
79 font du foot et de la natation :
- \(card(E_5)+card(E_8)=79\)
- \(card(E_5)+18=79\)
\(\Rightarrow card(E_5)=61\)
129 font de la natation dont 40 que de ça :
- \(card(E_3)+card(E_5)+card(E_7)+card(E_8)=129\)
- \(40+61+card(E_7)+18=129\)
\(\Rightarrow card(E_7)=10\)
103 ne font que 2 sports
- \(card(E_5)+card(E_6)+card(E_7)=103\)
- \(61+card(E_6)+10=103\)
\(\Rightarrow card(E_6)=32\)
200 élèves en tout :
- \(card(E_1)+card(E_2)+card(E_3)+card(E_4)+card(E_5)+card(E_6)+card(E_7)+card(E_8)=200\)
- \(10+card(E_2)+40+19+61+32+10+18=200\)
\(\Rightarrow card(E_2)=10\)
On obtient donc la partition suivante de l’ensemble des élèves pour la journée de sport :
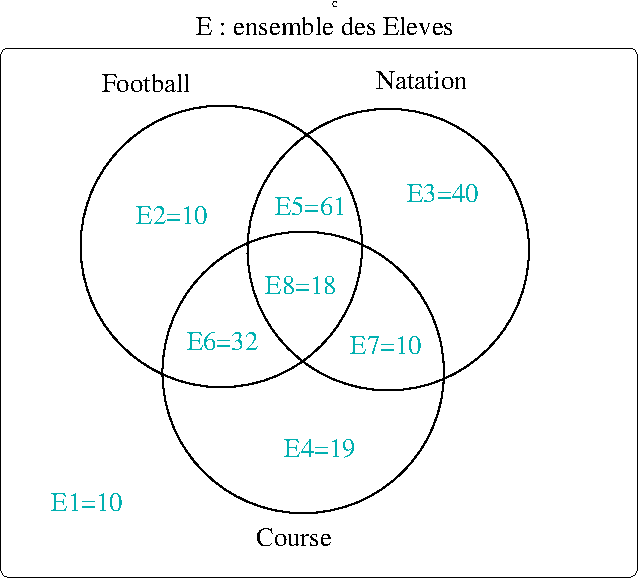
Notations
Dans la suite de ce cours nous adopterons une notation préfixée des opérations ensemblistes et autres :
- \(op(A,B)\)
plutôt que la notation infixée des opérations binaires :
- \(A \; op \; B\)
La notation préfixée sera en effet plus explicite pour représenter une opération ayant en entrée 2 ensembles pour générer en sortie un ensemble résultat :
- \(R=op(A,B)\)
Par exemple l’expression algébrique :
- \(R=(A \cup B) \setminus (A \cap B)\)
S’écrira :
- \(R=\setminus(\cup(A,B),\cap(A,B))\)
Et pourra se décomposer en :
- \(R_1=\cup(A,B)\)
- \(R_2=\cap(A,B)\)
- \(R=\setminus(R_1,R_2)\)
Par la suite on pourra représenter cette expression sous forme d’arbre de flux de données entre les opérateurs de l’algèbre relationnelle (\(\cup, \cap, \setminus ...\)).
Ces opérateurs, mis en œuvre dans les SGBD relationnels, serviront à éxécuter sur le serveur de bases de données les requêtes SQL.
Arbre de requêtes
L’expression algébrique suivante :
- \(R=\Pi_{(count(x))}(\setminus(\cup(A,B), \cap (A,B)))\)
utilisant les opérateurs de l’algèbre relationnelle :
- Projection (\(\Pi\)) : réduction du nombre d’informations sur les éléments de l’ensemble.
- Différence (\(\setminus\)) : opération ensembliste de différence entre deux ensembles.
- Intersection (\(\cap\)) : opération ensembliste d’intersection entre deux ensembles.
se représente sous forme d’arbre de flux de données. On pourra appliquer une fonction de calcul (count())
sur la racine de cet arbre (le résultat de la requête).
Si l’arbre de requêtes ci-dessous donne un résultat nul (count(x) = 0) alors les deux ensembles \(A,B\) sont égaux.
On notera la représentation graphique des opérateurs (noeuds de l’arbre) pour symboliser la projection (\(\Pi\)) et les opérations ensemblistes (\(\cup,\cap,\setminus\)).
On trouvera dans l’exercice ci-dessous un éditeur d’arbre de requêtes contenant une palette d’opérateurs de l’algèbre relationnelle permettant de construire vos arbres de requêtes.
Créer l’arbre de requêtes qui permettra de vérifier que les deux ensembles A et B , représentés ci-dessous, sont égaux.
Votre réponse :
Arbre de requêtes : AB.json
TablesOpérateurs unairesOpérateurs binaires |
| Vue d'ensemble | |
|---|---|
|
|
Produit cartésien
Définition du produit cartésien entre deux ensembles \(A,B\)
- \(A \times B = \{ (x,y) \; \vert \; (x \in A) \wedge (y \in B) \}\)
L’ensemble de tous les couples (2-uplets) dont la première composante est un élément du premier ensemble \(A\) et la deuxième un élément du deuxième ensemble \(B\). Chaque élément du premier ensemble est mis en relation avec tous les éléments du deuxième. On génère toutes les combinaisons possibles.
On notera par la suite le produit cartésien en notation préfixée :
- \(\times(A,B) = \{ (x,y) \; \mid \; (x \in A) \wedge (y \in B) \}\)
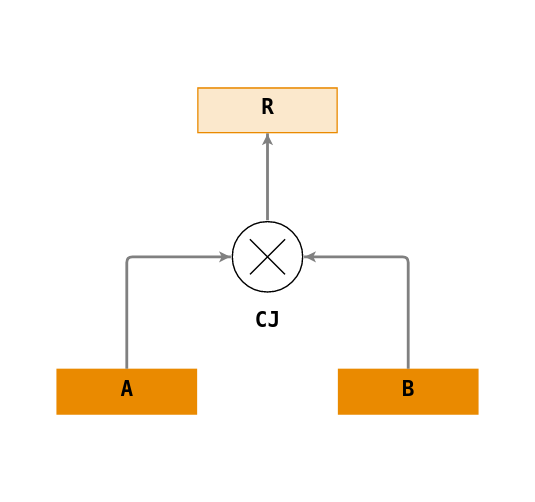
Représentation de l’opération produit cartésien sous forme d’arbre :
- \(R=\times(A,B)\)
Exemple de produit cartésien :
- \(A = \{2,4,6 \}, B = \{1,2,3,4,5,6 \}\)
- \(\times(A,B) = \{(2,1),(2,2),(2,3), ... , (6,4),(6,5),(6,6) \}\)
En SQL le produit cartésien (\(\times\)) s’exprime par un CROSS JOIN entre chaque table ou plus simplement par la liste des noms de table séparés par des virgules.
Autre exemple de produit cartésien inspiré des modèles de données proposés par Gardarin :
- \(\times(Cru,Couleur) = \times( \{'Sancerre','Chablis' \}, \{'blanc','rouge','rose' \} )\)
Autrement dit : tous les crus peuvent être produit en vins blanc, rouge ou rosé.
Relations
Tout sous-ensemble de produit cartésien :
- \(R(A,B) \subseteq \times(A,B)\)
- \(R(A,B) = \{(a,b) \; \mid \; (a,b) \in R \}\)
Exemple d’ensembles :
- \(A = \{2,4,6 \}, B = \{1,2,3,4,5,6 \}\)
Exemple de relation entre ensembles :
La relation : \(R(A,B) = \{(2,3),(2,4),(2,5),(2,6), (4,5) (4,6) \}\)
représente le sous-ensemble inférieur à du produit cartésien \(\times(A,B)\)
Ecriture en SQL du sous-ensemble inférieur à du produit cartésien \(\times(A,B)\) :
Domaine
Le domaine de la relation \(R \subseteq \times(A,B)\) se définit par l’ensemble des éléments de l’ensemble de départ qui sont en relation avec des éléments de l’ensemble d’arrivée.
- \(dom(R) = \{x \in A \; \vert \; \exists y \in B \; , \; (x,y) \in R \}\)
Ecriture en SQL du domaine de la relation inférieur à du produit cartésien \(\times(A,B)\) :
SELECT A.x AS "domain" FROM A,B WHERE A.x < B.y;
SELECT DISTINCT A.x AS "domain" FROM A,B WHERE A.x < B.y;
Image
L’image de la relation \(R \subseteq \times(A,B)\) se définit par l’ensemble des éléments de l’ensemble d’arrivée qui sont en relation avec des éléments de l’ensemble de départ :
- \(image(R) = \{ y \in B \; \vert \; \exists x \in A \; , \; (x,y) \in R \}\)
Ecriture en SQL de l’image de la relation inférieur à du produit cartésien \(\times(A,B)\) :
SELECT B.y AS "image" FROM A,B WHERE A.x < B.y;
SELECT DISTINCT B.y AS "image" FROM A,B WHERE A.x < B.y;
Fonction
Une relation \(R \subseteq (A \times B)\) est fonctionnelle si :
- \(\forall (x,y,y') \in (A \times B \times B), (x,y) \in R \wedge (x,y') \in R \Rightarrow y = y'\)
Autrement dit, une relation est fonctionnelle (fonction) si :
- au plus un élément de l’ensemble d’arrivée est associé à un élément de l’ensemble départ.
Autrement dit, une relation entre deux ensembles (\(A,B\)) est une fonction, notée \(f\) si :
- \(\forall x \in A\) il existe au plus un \(y \in B\) tel que \(y=f(x)\)
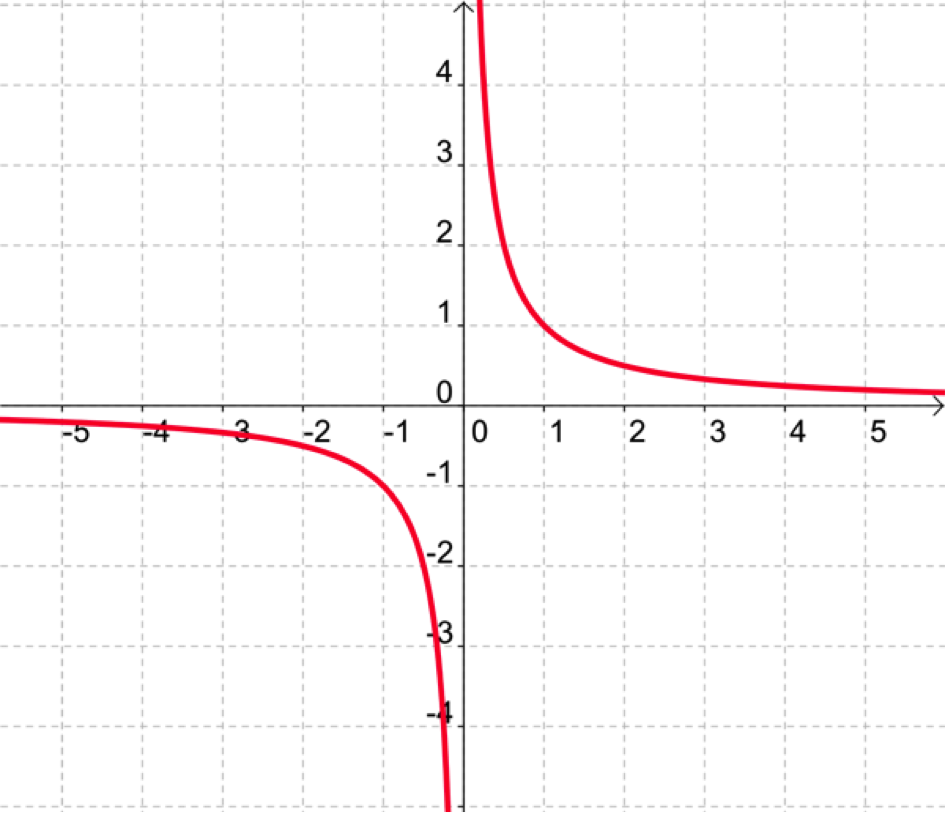
Exemple : la relation définie par \(y = 1/x\) est une fonction de \(\mathbb{R}\) vers \(\mathbb{R}\)
Comme on le voit sur le graphe de la fonction, les éléments de l’ensemble de départ (\(\mathbb{R}\)) sont au plus en relation avec un élément de l’ensemble d’arrivée (\(\mathbb{R}\)).
L’élément \(x=0\) est le seul élément de \(\mathbb{R}\) à ne pas avoir une (et une seule) image dans l’ensemble d’arrivée.
Application
Une relation fonctionnelle \(R \subseteq (A \times B)\) est applicative si :
- \(dom(R) = A\)
ou encore :
- \(\forall x \in A \; , \; \exists ! y \in B : (x,y) \in R\)
Autrement dit une relation fonctionnelle est applicative (est une application) si :
- Pour tout \(x \in A\) il existe un et un seul \(y \in B\) tel que \(y=f(x)\) (\(f\) : application)
- A chaque élément de l’ensemble de départ est associé un unique élément dans l’ensemble d’arrivée.
Ou encore :
- une application est une fonction définie partout
Exemple : la relation fonctionnelle définie par \(y = 1/x\) est une application de \(\mathbb{R}^*\) vers \(\mathbb{R}\)
Comme on le voit sur le graphe de la fonction, tous les éléments de l’ensemble de départ (\(\mathbb{R}^*\)) sont en relation avec un et un seul élément de l’ensemble d’arrivée (\(\mathbb{R}\)).
Injection
Une application \(f : A \rightarrow B\) est injective (injection) si et seulement si :
- \(\forall (x,y) \in (A \times B) \; : \; f(x)=f(y) \Rightarrow x=y\)
ou sa contraposée :
- \(\forall (x,y) \in (A \times B) \; : \; x \neq y \Rightarrow f(x) \neq f(y)\)
Autrement dit tout élément de l’image de la relation (l’ensemble d’arrivée) possède au plus un antécédent dans le domaine (ensemble de départ) de la relation.
Nous invitons le lecteur à trouver par lui-même un exemple d’application injective.
Surjection
Une application est surjective (surjection) si et seulement si :
- \(\forall y \in B \; , \; \exists x \in A \; , \; y=f(x)\)
L’image de la relation est l’ensemble d’arrivée : \(image(R) = B\).
Autrement dit tout élément de l’ensemble d’arrivée possède au moins un antécédent dans l’ensemble de départ.
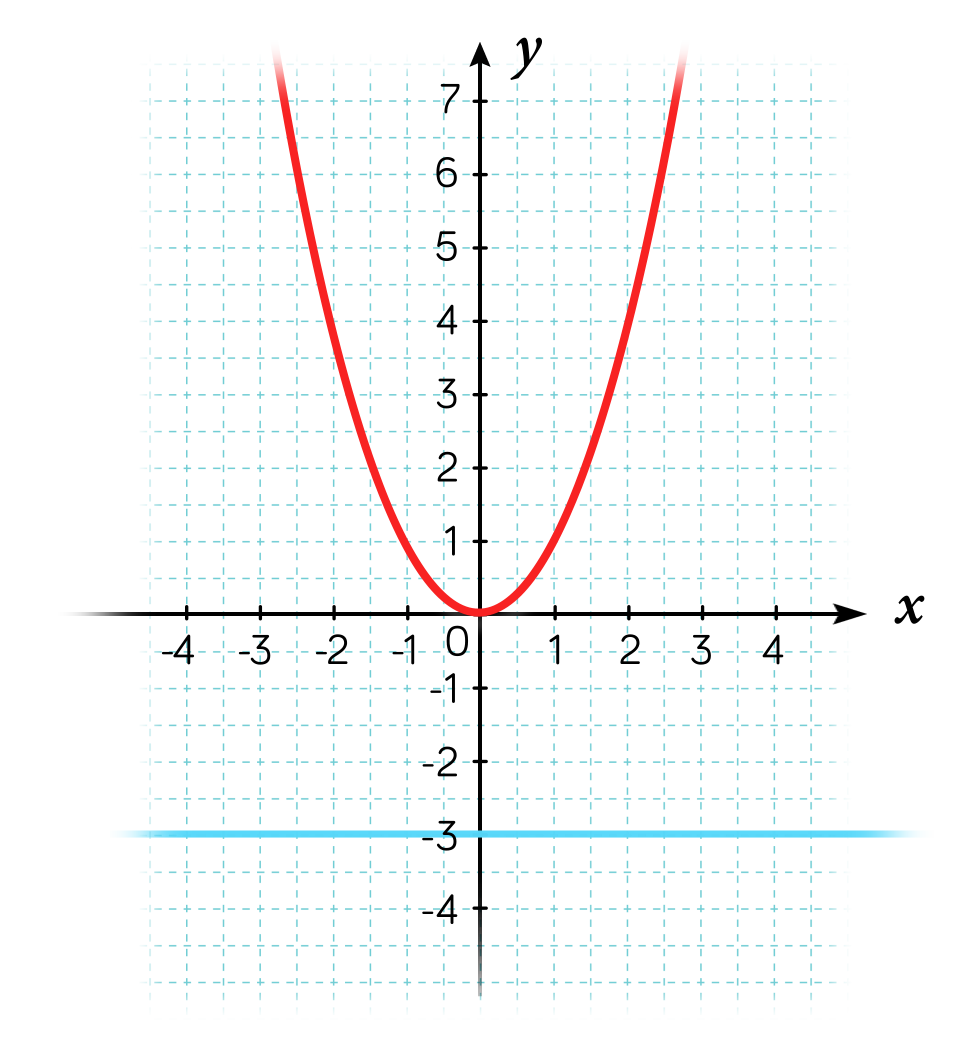
Exemple : l’application définie par \(y = x^2\) est une application surjective de \(\mathbb{R}\) vers \(\mathbb{R_+}\)
Comme on le voit sur le graphe de la fonction, tous les éléments de l’ensemble d’arrivée (\(\mathbb{R}_+\)) sont en relation avec au moins un élément de l’ensemble de départ (\(\mathbb{R}\)).
Bijection
Une application est bijective (injective et surjective} si et seulement si :
- \(\forall y \in B \; , \; \exists ! x \in A \; , \; y=f(x)\)
Autrement dit :
- tout élément de l’ensemble d’arrivée possède un et un seul antécédent dans l’ensemble de départ et réciproquement.
- l’application définie par \(y = x^3\) est une application surjective de \(\mathbb{R}\) vers \(\mathbb{R_+}\)
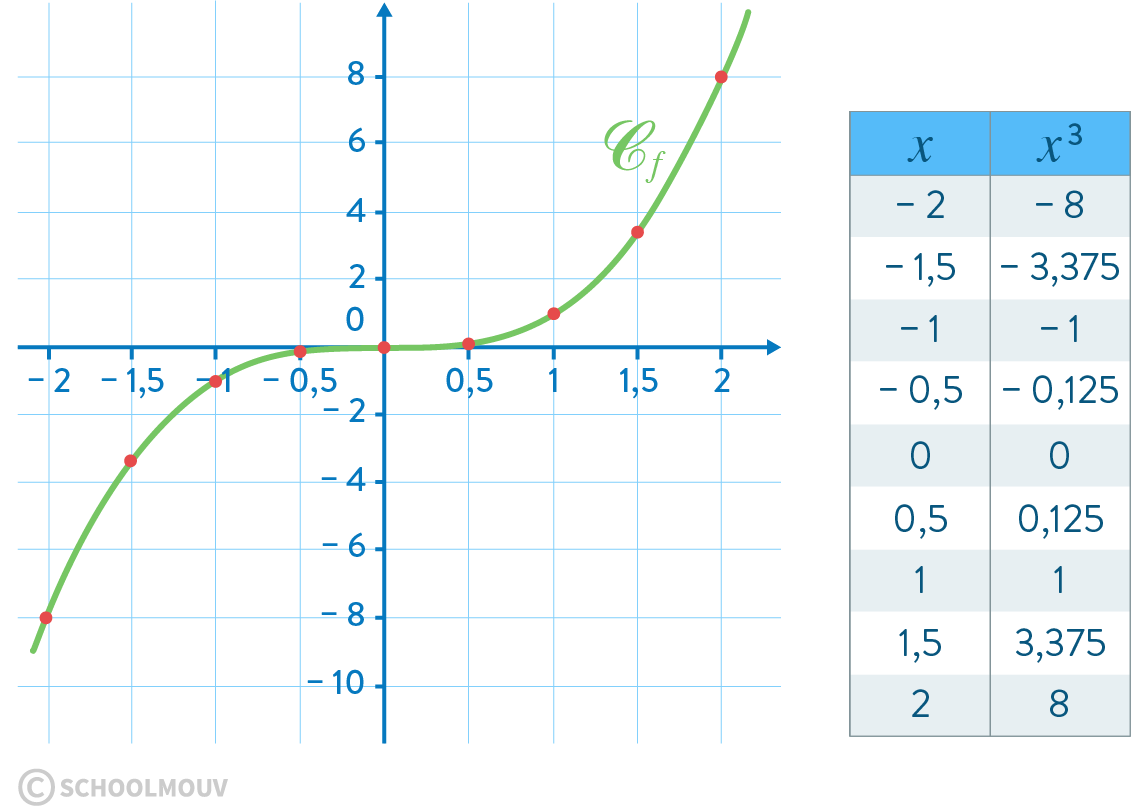
Comme on le voit sur le graphe de la fonction, tous les éléments de l’ensemble d’arrivée (\(\mathbb{R}\)) sont en relation avec un et un seul un élément de l’ensemble de départ (\(\mathbb{R}\)).
En résumé :
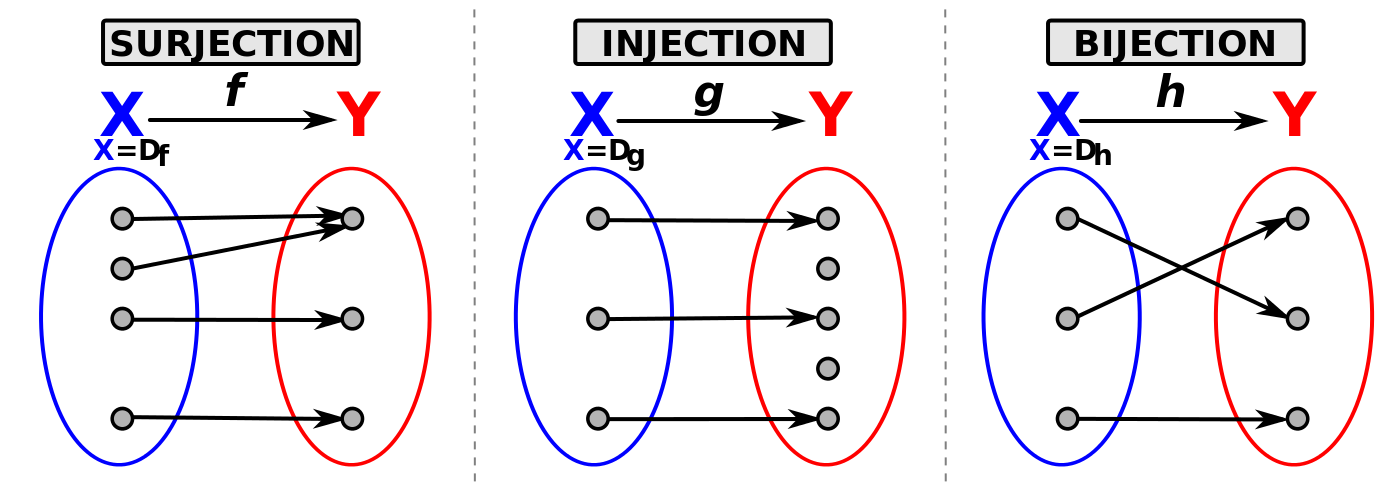
Diagramme de Venn pour une application injective,surjective et bijective :
Graphes de fonction pour une application injective, surjective et bijective :
Exemple :
Loger un ensemble de touristes (\(T\)) dans un ensemble de chambres d’hôtel (\(H\)).
Le responsable de l’hôtel souhaiterait une application (\(f : T \longrightarrow H\)) surjective :
- toutes les chambres sont occupées : il faut au moins autant de touristes que de chambres
Les touristes souhaitent une application (\(f : T \longrightarrow H\)) injective :
- chaque touriste veut une chambre pour lui, il faut au moins autant de chambres que de touristes
Ces deux contraintes ne sont compatibles que si l’application est bijective.
L’exrcice ci-dessous permettra au lecteur de se familiariser avec les notions d’applications injective, surjective, bijective.
Suivant les ensembles de départ et d’arrivée :
- \(f : \mathbb{R} \rightarrow \mathbb{R}\)
- \(f : \mathbb{R_+} \rightarrow \mathbb{R}\)
- \(f : \mathbb{R} \rightarrow \mathbb{R_+}\)
- \(f : \mathbb{R_+} \rightarrow \mathbb{R_+}\)
La fonction \(f : x \longrightarrow x^2\) est-elle :
- injective
- surjective
- bijective
- aucun des trois cas possibles
Votre réponse :
Zone de saisie de texte
| Clavier | Action |
|---|---|
| F1 | Afficher une aide technique |
| F2 | Afficher une aide pédagogique |
| Ctrl-A | Tout sélectionner |
| Ctrl-C | Copier la sélection dans le presse-papier |
| Ctrl-V | Copier le presse-papier dans la sélection |
| Ctrl-X | Couper la sélection et la copier dans le presse-papier |
| Ctrl-Z | Annuler la modification |
| Maj-Ctrl-Z | Rétablir la modification |
| Menu | Action |
|---|---|
| Ré-initialiser les sorties | |
| Faire apparaître le menu d'aide | |
| Valider la zone de saisie | |
| Initialiser la zone de saisie | |
| Charger le contenu d'un fichier dans la zone de saisie | |
| Sauvegarder le contenu de la zone de saisie dans un fichier | |
| Imprimer le contenu de la zone de saisie |
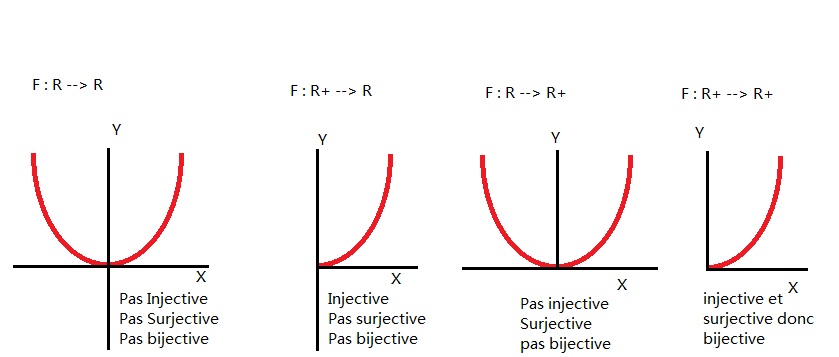
Une solution possible :
dans le premier cas (\(f : \mathbb{R} \rightarrow \mathbb{R}\)) la fonction (\(f : x \longrightarrow x^2\)) est :
- non-injective : deux éléments de l’ensemble de départ ont la même image \(\{ -1,+1 \} \rightarrow \{ +1 \}\)
- non-surjective : des éléments de l’ensemble d’arrivée n’ont pas d’antécédent (ex : \(y=-4\) n’a pas d’antécédent)
- non-bijective : puisque non-injective et non-surjective
dans le deuxième cas (\(f : \mathbb{R_+} \rightarrow \mathbb{R}\)) la fonction (\(f : x \longrightarrow x^2\)) est :
- injective : Les éléments de l’ensemble d’arrivée ont au plus un antécédent
- non-surjective : des éléments de l’ensemble d’arrivée n’ont pas d’antécédent (ex : \(y=-4\) n’a pas d’antécédent)
dans le troisième cas (\(f : \mathbb{R} \rightarrow \mathbb{R_+}\)) la fonction (\(f : x \longrightarrow x^2\)) est :
- non-injective : deux éléments de l’ensemble de départ ont la même image \(\{ -1,+1 \} \rightarrow \{ +1 \}\)
- surjective : tout élément de l’ensemble d’arrivée a au moins un antécédent
- non-bijective : puisque non-injective
dans le dernier cas (\(f : \mathbb{R_+} \rightarrow \mathbb{R_+}\)) la fonction (\(f : x \longrightarrow x^2\)) est :
- injective : Les éléments de l’ensemble d’arrivée ont au plus un antécédent
- surjective : tout élément de l’ensemble d’arrivée a au moins un antécédent
- bijective : puisque injective et surjective
Opérations ensemblistes
Les opérations ensemblistes permettent de répondre à des questions du type :
- Union (\(\cup\)) : donne-moi des éléments qui se trouvent dans deux ensembles
- intersection (\(\cap\)) : donne-moi des éléments qui sont commun à deux ensembles
- différence (\(\setminus\)) : donne-moi des éléments qui se trouve dans un ensemble mais ne font pas partie de l’autre.
Par exemple, considèrons dans une entreprise l’ensemble des personnes connues dans l’entrprise et l’ensemble des employés de l’entreprise.
Les opérations ensemblistes permettraient de retrouver ;
- Union (\(\cup\)) : les personnes et les employés de l’entreprise
- intersection (\(\cap\)) : les personnes qui sont des employés dans l’entreprise
- différence (\(\setminus\)) : les personnes qui ne sont pas des employés de l’entreprise
Ces opérations ensemblistes pourront également être exprimées par :
- des requêtes imbriquées (
IN, NOT IN, EXISTS, NOT EXISTS)- des jointures (
INNER JOIN, OUTER JOIN)
Comme nous le verrons lorsque nous aborderons le langage SQL plus en détail.
Union de deux ensembles
L’union de deux ensembles \(A\) et \(B\) est l’ensemble qui contient tous les éléments \(x\) qui appartiennent à \(A\) ou qui appartiennent à \(B\).
On la note classiquement \(A \cup B\).
- \(A \cup B = \{ x \mid ( x \in A ) \lor ( x \in B ) \}\)
Par la suite on utilisera la notation préfixée de l’opérateur binaire d’union :
- \(\cup(A,B) = \{ x \mid ( x \in A ) \lor ( x \in B ) \}\)
que l’on peut aussi écrire avec les fonctions caractéristiques (prédicats: \(P_A,P_B\)) :
- \(\cup(A,B) = \{ x \mid P_A(x) \lor P_B(x) \}\)
Par exemple l’union des ensembles \(A\) et \(B\) :
- \(A = \{ 1, 2, 3 \}, B = \{ 2, 3, 4 \}\)
est l’ensemble :
- \(R=\cup(A,B) = \{1, 2, 3, 4\}\).
Par défaut l’opérateur \(\cup\) élimine les doublons (éléments commun aux deux ensembles).
On peut également appliquer un UNION ALL si on ne veut pas les éliminer.
En logique booléenne l’union correspond à l’opérateur logique ou inclusif (\(\lor\)).
N.B: le ou est par défaut inclusif (en cas d’exclusion mutuelle on parlera de ou exclusif).
| Ou inclusif | ||
|---|---|---|
| A | B | A ou B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Intersection de deux ensembles
L’intersection de deux ensembles \(A\) et \(B\) est l’ensemble qui contient tous les éléments \(x\) qui appartiennent à \(A\) et qui appartiennent à \(B\).
On la note classiquement \(A \cap B\).
- \(A \cap B = \{ x \mid ( x \in A ) \land ( x \in B ) \}\)
Par la suite on utilisera la notation préfixée de l’opérateur binaire d’intersection :
- \(\cap(A,B) = \{ x \mid ( x \in A ) \land ( x \in B ) \}\)
que l’on peut aussi écrire avec les fonctions caractéristiques (prédicats: \(P_A,P_B\)) :
- \(\cap(A,B) = \{ x \mid P_A(x) \land P_B(x) \}\)
Par exemple l’intersection des ensembles \(A\) et \(B\) :
- \(A = \{1, 2, 3\}, B = \{2, 3, 4\}\)
est l’ensemble :
- \(R=\cap(A,B) = \{2, 3 \}\).
En logique booléenne l’intersection correspond à l’opérateur logique et (\(\land\)).
N.B: le et est par défaut exclusif (on parlera de et inclusif pour définir l’équivalence logique).
| ET (exclusif) | ||
|---|---|---|
| A | B | A et B |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Différence de deux ensembles
La différence entre deux ensembles \(A\) et \(B\) est l’ensemble qui contient les éléments \(x\) qui appartiennent à \(A\) et qui n’appartiennent pas à \(B\).
On la note classiquement \(A \setminus B\).
- \(A \setminus B = \{ x \mid ( x \in A ) \land ( x \notin B ) \}\)
Par la suite on utilisera la notation préfixée de l’opérateur binaire de différence :
- \(\setminus(A,B) = \{ x \mid ( x \in A ) \land ( x \notin B ) \}\)
que l’on peut aussi écrire avec les fonctions caractéristiques (prédicats: \(P_A , P_B\)) :
- \(\setminus(A,B) = \{ x \mid P_A(x) \land \neg P_B(x) \}\)
Par exemple la différence entre les ensembles \(A\) et \(B\) :
- \(A = \{1, 2, 3\}, B = \{2, 3, 4\}\)
est l’ensemble :
- \(R=\setminus(A,B) = \{1 \}\).
L’opérateur de différence n’est pas commutatif :
- \(R=\setminus(B,A) = \{4 \}\).
En logique booléenne la différence correspond à la négation de l’implication (\(\Rightarrow\)).
| Non implication | ||
|---|---|---|
| A | B | not(A => B) |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Implication : « A seulement si B »
- \((A \Rightarrow B) \Leftrightarrow (\neg A \lor B)\)
Non-implication : « A mais pas B »
- \(\neg (A \Rightarrow B) \Leftrightarrow (A \land \neg B)\)
L’implication sera présentée dans la partie « Logique » de ce chapitre.
Représentation des diagrammes de Venn pour l’union (\(\cup\)), l’intersection (\(\cap\)), la différence symétrique (ou exclusif, \(\oplus\)) et la différence (\(\setminus\)).
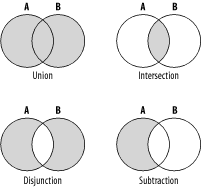
Disjonction exclusive (\(\oplus\)) :
- \(A \oplus B = \{ x \mid ( x \in A \land x \notin B ) \cup ( x \notin A \land x \in B ) \}\).
Table de vérité de l’opérateur (\(\oplus\)) :
| Ou exclusif | ||
|---|---|---|
| A | B | A xor B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Représentation du diagramme de Venn pour disjonction exclusive (\(\oplus\))
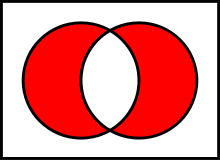
Ecriture d’une requête SQL pour obtenir une différence symétrique entre deux ensembles \(A,B\) :
Votre réponse :
Une solution possible :
SELECT * FROM A;
SELECT * FROM B;
-- A xor B --
SELECT x AS "A xor B" FROM A WHERE x NOT IN (SELECT y FROM B)
UNION
SELECT y FROM B WHERE y NOT IN (SELECT x FROM A);
Pour aller plus loin : on peut aussi exprimer la disjonction exclusive avec l’opérateur de jointure FULL OUTER JOIN mais cet opérateur n’est pas implémenté en SQLite par contre le lecteur intéressé pourra le tester sous PostgreSQL par exemple.
Les différentes jointures (INNER,OUTER,NATURAL) seront détaillées dans le chapitre SQL.
code SQL pour la disjonction exclusive à l’aide de jointure :
SELECT COALESCE(A.x, B.y) AS "A xor B"
FROM A FULL OUTER JOIN B
ON A.x = B.y
WHERE A.x IS NULL OR B.y IS NULL;
Propriétés des opérateurs ensemblistes :
L’union et l’intersection sont commutatives :
- \(\cup(A,B) = \cup(B,A)\)
- \(\cap(A,B) = \cap(B,A)\)
L’union et l’intersection sont associatives :
- \(\cup(A,\cup(B,C)) = \cup(\cup(A,B),C)\)
- \(\cap(A,\cap(B,C)) = \cap(\cap(A,B),C)\)
L’union est distributive par rapport à l’intersection :
- \(\cup(A,\cap(B,C)) = \cap(\cup(A,B),\cup(A, C))\)
L’intersection est distributive par rapport à l’union :
- \(\cap(A,\cup(B,C)) = \cup(\cap(A,B),\cap(A, C))\)
L’intersection est distributive par rapport à la différence :
- \(\cap(A,\setminus(B,C)) = \setminus(\cap(A,B),\cap(A, C))\)
Par contre :
La différence n’est pas commutative :
- \(\setminus(A,B) \neq \setminus(B,A)\)
La différence n’est pas associative :
- \(\setminus(A,\setminus(B,C)) \neq \setminus(\setminus(A,B),C)\)
L’union n’est pas distributive par rapport à la différence :
- \(\cup(A,\setminus(B,C)) \neq \setminus(\cup(A,B),\cup(A, C))\)
La différence n’est pas distributive par rapport à l’union :
- \(\setminus(A,\cup(B,C)) \neq \cup(\setminus(A,B),\setminus(A, C))\)
La différence n’est pas distributive par rapport à l’intersection :
- \(\setminus(A,\cap(B,C)) \neq \cap(\setminus(A,B),\setminus(A, C))\)
Multi-ensembles
Des requêtes sur les ensembles (tables) définis dans des bases de données relationnelles (ou simplement des tables sur lesquels ne seraient définies aucune contrainte d’unicité) peuvent produire des multi-ensembles, c’est à dire des ensembles sur lesquels un élément peut être présent plus d’une fois. Un multi-ensemble est donc une collection d’éléments non nécessairement distincts.
Un multi-ensemble peut-être défini comme un ensemble de paires (2-uplets) d’éléments représentant l’élément et sa multiplicité.
Un ensemble est un multi-ensemble dont la valeur de toutes les multiplicités est égale à 1.
Exemple :
le multi-ensemble :
- \(E=\{1,2,2,2,3,3 \}\)
de cardinalité \(card(E)=6\) peut-être défini par l’ensemble de 2-uplets :
- \(E=\{(1,1),(2,3),(3,2) \}\)
En SQL on peut représenter les multi-ensembles en faisant des regourpement GROUP BY :
Logique
Toute requête SQL sur une base de données sera exprimée par une formule de logique du premier ordre (logique des prédicats).
La logique du premier ordre, introduite par Gottlob Frege à la fin du 19ème siècle, permet de raisonner sur des énoncés du type :
- \(\exists x \forall y \; aime(x,y)\)
Cette formule logique voulant exprimer le fait que dans ce monde on trouvera au moins quelqu’un (\(x\)) qui aime tout le monde (\(y\)).
La logique du premier ordre utilise :
- des variables (\(x,y...\)) pour dénoter des éléments d’un ensemble.
- des prédicats (ou relations) sur (entre) les éléments.
- des connecteurs logiques et (\(\land\)), ou (\(\lor\)) …
- les quantificateurs existentiel,universel (\(\exists,\forall\))
- l’implication logique (si P alors Q) notée \(P \Longrightarrow Q\)
- des équivalences logiques (P si et seulement si Q) notée \(P \Longleftrightarrow Q\)
- …
Nous présentons dans cette partie les principales notions de logique nécessaires pour pouvoir exprimer par la suite des requêtes en calcul relationnel, algèbre relationnelle et langage SQL.
Une proposition logique (ou assertion) est une affirmation formée d’un assemblage de symboles et de mots à laquelle on peut clairement attribuer la valeur « vrai » ou « faux ».
Exemples de propositions :
- \(1+1=2\)
- tous les hommes sont mortels
- le coût du pétrole augmente mais pas le coût de la vie
- …
Le lecteur intéressé trouvera d’autres exemples de phrases de logique sur le site de Gérard Villemin.
L’exemple suivant sur la falsifiabilité d’une proposition scientifique est extrait d’un cours de logique de Bertrand Liaudet.
Certains philosophes disent qu’une proposition dont on dit qu’elle est vraie est scientifique si elle peut être réfutée, c’est-à-dire si on peut prouver sa négation. On dit qu’une proposition scientifique doit être falsifiable. Les propositions qui ne sont pas falsifiables sont des croyances.
Par exemple : « Le Mont Blanc est la plus haute montagne de France »
est une proposition scientifique. Pour prouver le contraire, il suffit de trouver une montagne plus haute.
Autre exemple : « Les extraterrestres n’existent pas ».
est une proposition qui peut être vraie ou fausse. Si on considère qu’elle est vraie, alors son contraire : « les extraterrestres existent » est faux.
Cette dernière proposition est « facilement » prouvable : il suffit d’en trouver un ! Comme on n’en a toujours pas trouvé, la proposition :
- « les extraterrestres n’existent pas ».
est une proposition scientifique vraie jusqu’à preuve du contraire. Il en va de même pour les dragons et les fantômes !
Par contre la proposition : « les extraterrestres existent ».
est également une proposition qui peut être vraie ou fausse et son contraire est : « les extraterrestres n’existent pas ».
Comment prouver cette proposition ? Il faudrait parcourir l’univers tout entier dans tous ses recoins ! Impossible. Donc la proposition :
- « les extraterrestres existent »
n’est pas une affirmation scientifique : c’est une croyance.
Il en va de même pour l’existence des dragons, des fantômes et autres créatures dont on n’a pas encore trouvé trace.
Donc, la seule proposition scientifique possible est :
- « les extraterrestres n’existent pas »,
au moins jusqu’à preuve du contraire. Ca n’empêche pas d’y croire !
Par définition une proposition, notée \(P\), satisfait les 3 principes (axiomes) :
Principe d’identité :
- si \(P\) est vrai alors \(P\) est vrai et si \(P\) est faux alors \(P\) est faux.
- autrement dit : « ce qui est vrai est vrai », « si c’est faux, c’est faux »
Principe de non contradiction :
- \(P\) ne peut pas à la fois être vrai et faux.
- autrement dit : « on ne peut affirmer une chose et son contraire à la fois »
Principe du tiers exclus :
- soit \(P\) est vrai, soit \(P\) est faux. Il n’existe pas d’autre valeur de vérité en logique mathématique.
- autrement dit : « c’est vrai ou c’est faux un point c’est tout ! »
Implication logique entre deux propositions, notée \(P \Rightarrow Q\) :
- la proposition (\(P \Rightarrow Q\)) est fausse seulement lorsque la proposition \(P\) est vraie et la proposition \(Q\) est fausse.
- l’implication (\(P \Rightarrow Q\)) peut s’interpréter : \(P\) seulement si \(Q\)
Table de vérité :
| Implication | ||
|---|---|---|
| P | Q | P => Q |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Equivalence logique de l’implication:
- \((P \Rightarrow Q) \Leftrightarrow (\neg P \lor Q)\)
- si la proposition \(P\) est vraie alors la proposition \(Q\) doit être vraie (pour que l’implication soit vraie)
On dit que :
- \(P\) implique \(Q\)
- si \(P\) alors \(Q\)
- \(P\) entraîne \(Q\)
- on ne peut avoir à la fois \(P\) vraie et \(Q\) fausse.
- si \(P\) est vraie alors \(Q\) ne peut être fausse.
- pour que \(P\) il faut que \(Q\)
- \(Q\) est une condition nécessaire pour avoir \(P\), dès que \(P\) est vraie, alors nécessairement, forcément, obligatoirement \(Q\) doit être vraie pour que l’implication le soit
- \(P\) est une condition suffisante pour que \(Q\) mais non nécessaire pour que l’implication soit vraie (\(P\) faux ne veut pas dire nécessairement que \(P \Rightarrow Q\) est faux).
Remarque : on emploie souvent il faut à la place de il suffit, par exemple :
- « pour traverser la rivière, il faut prendre le bateau »
alors que c’est suffisant mais pas nécessaire… on peut très bien le faire à la nage !
On devrait dire :
- « pour traverser la rivière, il suffit de prendre le bateau »
une condition suffisante pour traverser la rivière (proposition \(Q\)) est de prendre le bateau (proposition \(P\))
une condition nécessaire pour prendre le bateau (proposition \(P\)) est de vouloir traverser la rivière (proposition \(Q\))
Si je prends le bateau alors je traverse la rivère.
Exemple d’implication à partir des propositions suivantes :
- proposition \(P\) : « avoir le diplôme de l’ENIB »
- proposition \(Q\) : « avoir passé cinq années d’études »
Une condition nécessaire pour avoir le diplôme de l’ENIB est d’avoir passé cinq années d’études.
Par contre ce n’est pas suffisant, on peut malheureusement passer plus de cinq années avant d’avoir le diplôme d’ingénieur ENIB.
Une condition suffisante pour avoir passé cinq années d’études est d’avoir le diplôme de l’ENIB (mais ce n’est pas nécessaire,on peut très bien aller dans une autre école à bac+5 même si on est bien à l’ENIB).
Par contre, il ne suffit pas d’avoir passé cinq années d’études pour avoir le diplôme de l’ENIB … ça serait quand-même un peu trop facile !
Autrement dit, avoir passé cinq années d’études (\(Q\)) est une condition nécessaire mais non-suffisante pour avoir le diplôme de l’ENIB (\(P\))
L’ensemble des étudiants diplômés de l’ENIB est un sous-ensemble de l’ensemble des étudiants qui ont passé cinq années d’études (même si l’idéal serait que ces deux ensembles soient égaux mais, dans ce cas, ce ne serait plus une implication mais une équivalence logique dont la définition sera vue plus loin dans ce chapitre).
Autre exemple d’implication à partir des propositions suivantes : :
- proposition \(P\) : \(n > 2 \land n \; premier\)
- proposition \(Q\) : \(n \; impair\)
Pour que \(P\) il est nécessaire que \(Q\) : pour que (\(n > 2 \land n \; premier\)) il est nécessaire que \(n\) soit un nombre impair
Il ne suffit pas que \(Q\) pour que \(P\) : il ne suffit pas que \(n\) soit un nombre impair pour qu’il soit un nombre premier supérieur à deux
La contraposée de l’implication \(P \Rightarrow Q\) :
- \(\neg Q \Rightarrow \neg P\)
Exemples :
- implication :
- \(P \Rightarrow Q\) : s” il pleut, alors le sol est mouillé
- contraposée :
- \(\neg Q \Rightarrow \neg P\) : si le sol n’est pas mouillé, alors il ne pleut pas
- implication :
- proverbe : pas de problème sans solution
- \(P \Rightarrow Q\) : s’il y a un problème alors il y a une solution
- contraposée :
- \(\neg Q \Rightarrow \neg P\) : s’il n’y a pas de solution, c’est qu’il n’y a pas de problème
- c’est un des proverbes de Shadoks
La contraposée de l’implication est équivalente à l’implication :
- \((P \Rightarrow Q) \Leftrightarrow (\neg Q \Rightarrow \neg P)\)
Démonstration :
- \((P \Rightarrow Q) \Leftrightarrow (\neg P \lor Q)\)
- \((\neg Q \Rightarrow \neg P) \Leftrightarrow (\neg(\neg Q) \lor \neg P)\)
- \((\neg(\neg Q) \lor \neg P) \Leftrightarrow Q \lor \neg P\)
- \(Q \lor \neg P \Leftrightarrow (\neg P \lor Q)\)
Exercice :
- Montrez, à l’aide de tables de vérité, que la contraposée de l’implication a les mêmes valeurs de vérité que l’implication.
La réciproque de l’implication \(P \Rightarrow Q\) :
- \(Q \Rightarrow P\)
Exemples :
- implication : s” il pleut, alors le sol est mouillé
- réciproque : le sol est mouillé alors il pleut
- implication : s’il y a un problème alors il y a une solution
- réciproque : s’il y a solution alors il y a un problème
La négation de l’implication \(P \Rightarrow Q\) :
- \(\neg (P \Rightarrow Q) \Leftrightarrow \neg ( \neg P \lor Q) \Leftrightarrow P \land \neg Q\)
Exemples :
- implication : s” il pleut, alors le sol est mouillé )
- négation : il pleut et le sol n’est pas mouillé
- implication : s’il y a un problème alors il y a une solution
- négation : il y a problème ET il n’y a pas de solution
Exemples en mathématiques :
- implication : (\(n\) est un nombre premier et \(n \neq 2\)) \(\Rightarrow\) (\(n\) est un nombre impair) : vraie
- contraposée : (\(n\) est un nombre pair) \(\Rightarrow\) (\(n\) n’est pas un nombre premier ou \(n = 2\)) : vraie
- réciproque : (\(n\) est un nombre impair) \(\Rightarrow\) (\(n\) est un nombre premier et \(n \neq 2\)) : faux
- négation : (\(n\) est un nombre premier et \(n \neq 2\)) ET (\(n\) est un nombre pair) : faux
- Soit deux propositions \(P,Q\) telles que :
- \(P \Rightarrow Q\) : « P est une condition suffisante de Q »
- \(Q \Rightarrow P\) : « P est une condition nécessaire de Q »
En logique classique, deux propositions \(P\) et \(Q\) sont dites logiquement équivalentes ou simplement équivalentes quand il est possible de déduire \(Q\) à partir de \(P\) et de déduire \(P\) à partir de \(Q\). Autrement dit :
- \(P \Leftrightarrow Q = (P \Rightarrow Q) \land (Q \Rightarrow P))\)
Cela revient à dire que \(P\) et \(Q\) ont même valeur de vérité : \(P\) et \(Q\) sont soit toutes les deux vraies, soit toutes les deux fausses. L’équivalence logique s’exprime souvent sous la forme si et seulement si.
Table de vérité :
| Equivalence logique | ||
|---|---|---|
| P | Q | P <=> Q |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Autre appellation de l’équivalence logique :
et-inclusif : le cas ou les deux propositions sont fausses est vraie, pour qu’elles puissent être équivalentes.
nxor (ou xnor) : c’est la négation du ou exclusif (xor) :
- \(P \oplus Q = (P \land \neg Q) \lor (\neg P \land Q)\)
- \(\neg (P \oplus Q) = \neg ((P \land \neg Q) \lor (\neg P \land Q))\)
- \(\neg (P \oplus Q) = (\neg P \lor Q) \land (P \lor \neg Q))\)
- \(\neg (P \oplus Q) = (P \Rightarrow Q) \land (Q \Rightarrow P))\)
CQFD !
La logique des prédicats, encore appelée logique du premier ordre, permet d’écrire des propositions avec des variables :
- certains chats sont gris :
- \(\exists x, chats(x) \land gris(x)\)
- Tous les humains sont mortels :
- \(\forall x, humains(x) \Rightarrow mortels(x)\)
- \(\forall x, x \in \mathbb{R}, \exists y \in \mathbb{R}, y>x\) : quelque soit le réel \(x\), il existe un réel \(y\) tel que \(y>x\)
- …
La logique des prédicats fait apparaître les quantificateurs universel ( \(\forall\)) et existentiel (\(\exists\)).
Une proposition prédicative peut s’écrire :
- \(\forall x, P(x)\) : la proposition \(P\) est vérifiée quel que soit l’élément \(x\)
- \(\exists x, P(x)\) : il existe un élément \(x\) pour lequel la proposition \(P\) est vérifiée
Règle d’écriture d’une proposition prédicative :
- Les quantificateurs sont à placer avant les prédicats
Même si les cas précédents sont bien formulés on peut, pour plus de clarté on peut ré-écrire :
- \(\forall x,\exists y (x \in \mathbb{R}, y \in \mathbb{R}), y>x)\)
où la proposition prédicative est :
- \((x \in \mathbb{R}, y \in \mathbb{R}),y>x\)
qui s’interprèterait :
- pour tout \(x\), il existe \(y\) tel que : SI \(x \in \mathbb{R}\) et \(y \in \mathbb{R}\) ALORS \(y>x\)
Le quantificateur existentiel s’exprime par la formule logique suivante :
- \(\exists x \in E, P(x)\)
ou en plus condensé :
- \(\exists x, P(x)\)
En SQL le quantificateur existentiel est représenté par EXISTS.
SELECT nom FROM sportifs
WHERE EXISTS (SELECT * FROM activites WHERE sportifs.sport=activites.sport);
La requête ci-dessus reviendrait à chercher le nom des sportifs qui font au moins une activité sportive.
Le quantificateur universel s’exprime par la formule logique suivante :
- \(\forall x, P(x)\)
En SQL le quantificateur universel … n’existe pas.
On pourra cependant le formuler à l’aide d’opérateurs de base de l’algèbre relationnelle.
Le quantificateur universel correspond à l’opérateur de division relationnelle qui sera détaillée dans le chapitre Algèbre relationnelle.
On pourra utiliser les équivalences logiques ci-dessous pour traduire un quantificateur universel en quantificateur existentiel et réciproquement.
- \(\forall x, P(x) \Leftrightarrow \neg (\exists x, \neg P(x))\)
- \(\exists x, P(x) \Leftrightarrow \neg (\forall x, \neg P(x))\)
Ainsi pour rechercher :
- le nom des sportifs qui seraient inscrit à toutes (\(\forall\)) les activités proposées
On pourrait reformuler cette question par un quantificateur existentiel (\(\exists\)) et une double négation :
- le nom des sportifs pour lesquels il n’existe pas d’activités auxquelles ces sportifs ne seraient pas inscrits
Ce qui se formulerait en SQL :
SELECT nom
FROM sportifs s1
WHERE NOT EXISTS (
SELECT * FROM activites
WHERE NOT EXISTS (
SELECT * FROM sportifs s2
WHERE s2.sport=activites.sport AND s1.nom=s2.nom
)
);
Si vous n’arrivez pas à comprendre cette requête SQL, pas d’inquiétude, nous reviendrons plus tard sur la mise en oeuvre de ce genre de requête pour représenter l’opérateur de division relationnelle.
Traduisez en proposition et implication la phrase suivante :
- « Pour que les étudiants réussissent, il faut qu’ils étudient. »
Faites la table de vérité correspondant et interpréter tous les cas.
Votre réponse :
Zone de saisie de texte
| Clavier | Action |
|---|---|
| F1 | Afficher une aide technique |
| F2 | Afficher une aide pédagogique |
| Ctrl-A | Tout sélectionner |
| Ctrl-C | Copier la sélection dans le presse-papier |
| Ctrl-V | Copier le presse-papier dans la sélection |
| Ctrl-X | Couper la sélection et la copier dans le presse-papier |
| Ctrl-Z | Annuler la modification |
| Maj-Ctrl-Z | Rétablir la modification |
| Menu | Action |
|---|---|
| Ré-initialiser les sorties | |
| Faire apparaître le menu d'aide | |
| Valider la zone de saisie | |
| Initialiser la zone de saisie | |
| Charger le contenu d'un fichier dans la zone de saisie | |
| Sauvegarder le contenu de la zone de saisie dans un fichier | |
| Imprimer le contenu de la zone de saisie |
Une solution possible :
On peut reformuler la phrase : « Pour que les étudiants réussissent, il faut qu’ils étudient. »
par : « Si les étudiants étudient alors ils réussissent »
D’où les propositions :
- \(P\) : « les étudiants étudient »
- \(Q\) : « les étudiants réussissent »
En représentant la table de vérité de l’implication (Si P alors Q) :
Implication P Q P => Q 0 0 1 0 1 1 1 0 0 1 1 1
On peut interpréter les différents cas :
- \(P,Q\) sont toutes deux fausses : les étudiants n’étudient pas et ils ne réussissent pas (c’est classique !)
- \(P\) fausse, \(Q\) vraie : les étudiants n’étudient pas et ils réussissent (ça arrive, mais c’est rare !)
- \(P\) vraie, \(Q\) fausse : les étudiants étudient et ils ne réussissent pas (ce n’est pas possible !)
- \(P\) vraie, \(Q\) vraie : les étudiants étudient et ils réussissent (c’est normal !)