Fichier de rejeu Close

Indication Close

A propos de... Close

Commentaire Close

Systèmes d'Information

Liste des projets

Index

Aide

Menu	Contenu
	Sommaire, Téléchargements
	Aide sur les outils

Chevron	Action
	Aller en haut de la page courante
	Aller en bas de la page courante
	Passer à la page précédente
	Passer à la page suivante

Calcul relationnel

Le calcul relationnel est une notation logique, où l’on exprimera les requêtes par la formulation de restrictions logiques que les éléments (tuples) retenus dans la réponse à la requête devront satisfaire.

Définition

On distingue :

Calcul Relationnel de Domaine (DRC) : les variables sont les attributs des n-uplets (tuples).

exemple : \(x \in Personnes.nom\)

cette représentation de requêtes est issue des travaux sur le langage QBE (IBM)

calcul relationnel de tuples (TRC): les variables sont les éléments (n-uplets).

exemple : \(x \in Personnes\)

cette représentation de requêtes est issue des travaux sur le langage QUEL (INGRES)

Le DRC est un langage d’interrogation de données formel permettant d’exprimer des questions à partir de formules bien formées dont chaque variable est interprétée comme variant sur le domaine d’un argument d’un prédicat.

Une question en calcul relationnel de domaine s’écrit sous la forme :

\(\{(x,y,...) \; \mid \; F(x,y, ...)\}\)

où :

\(F\) : est une formule logique
\((x,y ...)\) : variables libres dans \(F\)

ex: 'produits'

produits(id_prod, nom, quantite, couleur)

nom et couleur de tous les produits :

\(R=\{(n,c) \mid produits(-,nom:n,-,couleur:c)\}\)

nom et quantite en stock des produits de couleur rouge :

\(R=\{(n,q) \mid produits(-,nom:n,quantite:q,couleur="rouge")\}\)

Le TRC est un langage d’interrogation de données formel permettant d’exprimer des questions à partir de formules bien formées dont les variables sont interprétées comme variant sur les éléments (n-uplets) d’une table.

Une question en calcul relationnel de tuples s’écrit sous la forme :

\(\{(t_1.x,t_1.y,t_2.u,t_2.v,...) \; \mid \; F(t_1,t_2 ....) \}\)

ou bien :

\(\{(t.x,t.y,t_2.u,t_2.v,...) \; \mid \; t_1 \in T_1 \land t_2 \in T_2 \; ... \}\)

où :

\(F\) : est une formule logique sur des éléments (tuples) des ensembles \(T_1,T_2,...\)

\((t_1.x,t_1.y,t_2.u,t_2.v...)\) : attributs des n-uplets (tuples) des ensembles \(T_1,T_2,...\)

ex: 'produits'

produits(id_prod, nom, quantite, couleur)

nom et couleur de tous les produits :

\(R=\{(p.nom,p.couleur) \mid produits(p)\}\)

ou :

\(R=\{(p.nom,p.couleur) \mid p \in produits\}\)

nom et quantite en stock des produits de couleur "rouge" :

\(R=\{(p.nom,p.quantite) \mid produits(p) \land p.couleur="rouge"\}\)

ou :

\(R=\{(p.nom,p.quantite) \mid p \in produits \land p.couleur="rouge"\}\)

Toute requête sur une base de données peut être exprimée par une formule de logique du premier ordre en calcul relationnel.

Les opérateurs de l’algèbre relationnelle qui seront utilisés pour formuler des requêtes sur une base de données peuvent être formalisés en calcul relationnel :

Projection : réduire le nombre d’attributs (\(a_1,...,a_n\)) sur les éléments d’un ensemble (\(E\))
- \(\Pi_{(a_1,...,a_n)}(E)=\{ (e.a_1,....,e.a_n) \; | \; e \in E \}\)
Restriction : récupérer les éléments (\(e\)) d’un ensemble (\(E\)) qui satisfont un critère de restriction \([p(e)]\)
- \(\sigma_{[p(e)]}(E)=\{ e \; | \; e \in E \land p(e) \}\)
Produit cartésien : mettre en relation chaque élément de l’ensemble \(S\) avec tous les éléments de l’ensemble \(T\)
- \(\times(S,T)=\{ (s,t) \; | \; s \in S \land t \in T \}\)
Union : créer l’ensemble contenant les éléments qui sont dans l’ensemble \(S\) et dans l’ensemble \(T\)
- \(\cup(S,T)=\{ r \; | \; r \in \Pi_{(s_1,...,s_n)}(S) \lor r \in \Pi_{(t_1,...,t_n)}(T) \}\)

Les éléments des deux ensembles ont le même nombre d’attributs définis sur le même domaine.

Différence : créer l’ensemble contenant les éléments de l’ensemble \(S\) qui ne sont pas dans l’ensemble \(T\)
- \(\setminus(S,T)=\{ r \; | \; r \in \Pi_{(s_1,...,s_n)}(S) \land r \notin \Pi_{(t_1,...,t_n)}(T) \}\)

Les éléments des deux ensembles ont le même nombre d’attributs définis sur le même domaine.

Intersection : créer l’ensemble contenant uniquement les éléments de l’ensemble \(S\) qui sont aussi dans l’ensemble \(T\)
- \(\cap(S,T)=\{ r \; | \; r \in \Pi_{(s_1,...,s_n)}(S) \land r \in \Pi_{(t_1,...,t_n)}(T) \}\)

Les éléments des deux ensembles ont le même nombre d’attributs définis sur le même domaine.

Jointure : mettre en relation les éléments \((s,t)\) des ensembles \((S,T)\) s’ils satisfont un critère de jointure \([p(s,t)]\)
- \(\Join_{[p(s,t)]}(S,T)=\{ (s,t) \; | \; s \in S \land t \in T \land p(s,t) \}\)
Division relationnelle : récupérer les éléments (\(r\)) des éléments (\(s=(r,t)\)) de l’ensemble \(S\) qui sont en relation avec tous les éléments (\(t\)) de l’ensemble \(T\)
- \(\div(S,T)=\{r \; | \; \forall t \in T, (r,t) \in S \}\)

où l’ensemble des attributs de \(T\) est un sous-ensemble de l’ensemble des attributs de \(S\) (\(attr(T) \subset attr(S)\))

Aux pays des bières

On formulera ici les recherches d’information en calcul relationnel sur le modèle de données des « bars qui servent des bières ».

On pourra vérifier le résultat sur une base de données SQLite en formulant les requêtes SQL.

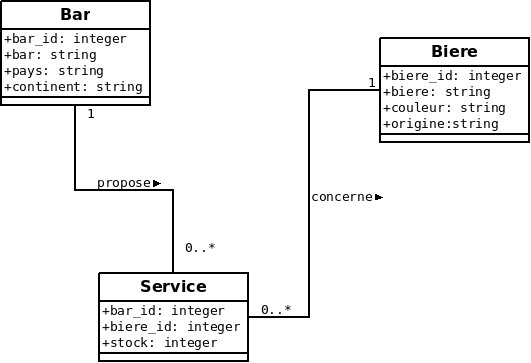
Faire le diagramme de classes et les commandes SQL de création des tables du modèle données :

Un bar a un nom (bar), est localisé dans un pays (pays),
Une bière a un nom (biere), une couleur (couleur) et un pays d’origine de fabrication (origine),
un service contient les quantités (stock) de bières servies dans les bars.

Diagramme de classes

Création des tables SQL

CREATE TABLE bars (
                   id_bar INTEGER NOT NULL PRIMARY KEY,
                   bar VARCHAR(20),
                   pays  VARCHAR(20)
                  );

CREATE TABLE bieres (
                     id_biere INTEGER NOT NULL PRIMARY KEY,
                     biere VARCHAR(20),
                     couleur VARCHAR(10),
                     origine VARCHAR(20)
                    );

CREATE TABLE services (
                       id_bar INTEGER NOT NULL,
                       id_biere INTEGER NOT NULL,
                       stock SMALLINT,
                       PRIMARY KEY (id_bar, id_biere),
                       FOREIGN KEY (id_bar)   REFERENCES bars,
                       FOREIGN KEY (id_biere) REFERENCES bieres
                      );

Calcul relationnel :

rechercher les informations suivantes sur le modèle de données en écrivant les requêtes en calcul relationnel et en langage SQL.

nom et couleur des bières

Calcul relationnel de domaine :

\(R=\{ (b,c) \; | \; bieres(-,biere:b,couleur:c,-) \}\)

Calcul relationnel de n-uplets :

\(R=\{ (b.biere,b.couleur) \; | \; b \in bieres \}\)

SQL :

SELECT couleur,biere FROM bieres;

bières françaises

Calcul relationnel de domaine :

\(R=\{ (id,b,c,o) \; | \; bieres(id\_biere:id,biere:b,couleur:c,origine="France":o) \}\)

Calcul relationnel de n-uplets :

\(R=\{ b \; | \; b \in bieres \land origine="France" \}\)

SQL :

SELECT * FROM bieres WHERE origine='France';

toutes les combinaisons possibles de bars et de bières

Calcul relationnel de domaine :

\(R= \{ (id\_ba,ba,p,id\_bi,bi,c,o) \; | \; bars(id\_bar:id\_ba,bar:ba,pays:p) \land bieres(id\_biere:id\_bi,biere:bi,couleur:c,origine:o) \}\)

Calcul relationnel de n-uplets :

\(R= \{ (ba,bi) \; | \; ba \in bars \land bi \in bieres \}\)

SQL :

SELECT * FROM bars, bieres;
-- ou
SELECT * FROM bars CROSS JOIN bieres;

nom des pays qui ont des bars et nom de l'origine de production des bières

Calcul relationnel de domaine :

\(R= \{ nom \; | \; bars(-,-,pays:nom) \lor bieres(-,-,-,origine:nom) \}\)

Calcul relationnel de n-uplets :

\(R=\{ nom \; | \; (b.pays:nom, b \in bars) \lor (b.origine:nom, b \in bieres) \}\)

SQL :

SELECT pays AS nom FROM bars
UNION
SELECT origine AS nom FROM  bieres;

les pays qui ont des bars et qui ne produisent pas de bière

Calcul relationnel de domaine :

\(R= \{ nom \; | bars(-,-,pays:nom) \land \neg bieres(-,-,-,origine:nom) \}\)

Calcul relationnel de n-uplets :

\(R=\{ nom \; | \; (b.pays:nom, b \in bars) \land \neg (b.origine:nom, b \in bieres)\}\)

SQL :

(SELECT pays AS nom FROM bars)
EXCEPT
(SELECT origine AS nom FROM  bieres);

les pays qui ont des bars et qui produisent de la bière

Calcul relationnel de domaine :

\(R= \{ nom \; | \; bars(-,-,pays:nom) \land bieres(-,-,-,origine:nom) \}\)

Calcul relationnel de n-uplets :

\(R=\{ (nom \; | \; (b.pays:nom, b \in bars) \land (b.origine:nom, b \in bieres) \}\)

SQL :

(SELECT pays AS nom FROM bars)
INTERSECT
(SELECT origine AS nom FROM  bieres);

les noms des pays qui ont des bars et qui sont aussi des pays qui produisent de la bière

Calcul relationnel de domaine :

\(R= \{ nom \; | \; bars(-,-,pays:nom) \land \exists \; o \; bieres(-,-,-,origine:o=nom) \}\)

Calcul relationnel de n-uplets :

\(R=\{ nom \; | \; (ba.pays:nom, ba \in bars) \land (bi.origine:nom, bi \in bieres) \land ba.pays=bi.origine\}\)

SQL :

SELECT pays AS nom FROM bars INNER JOIN bieres ON(pays=origine);
-- ou
SELECT pays AS nom FROM bars,bieres WHERE pays=origine;

le nom des bars qui servent toutes les bières

Calcul relationnel de domaine :

\(R=\{nom \; | \; bars(id\_bar:id_\_ba,bar:nom,-,-) \land \; \forall \; id\_bi \; bieres(id\_biere:id\_bi,-,-,-), services(id\_ba,id\_bi,-)) \}\)

Calcul relationnel de n-uplets :

\(R=\{ba.bar \; | ba \in bars \land \; (\forall bi \in bieres \; , \; (ba,bi) \in services) \}\)

SQL :

L’opérateur n’existe pas en SQL mais peut être exprimé par une double négation (NOT EXISTS)

« Trouver les bars tel qu” il n’existe pas de bière pour laquelle il n’existe pas de service associant ce bar et cette bière »

SELECT *
FROM bars ba
WHERE NOT EXISTS( SELECT *
                  FROM bieres bi
                  WHERE NOT EXISTS( SELECT *
                                    FROM services s
                                    WHERE s.id_bar=ba.id_bar
                                      AND s.id_biere=bi.id_biere
                                  )
                );

NB : pour plus d’information sur la division relationnelle on pourra se reporter à la section correspondante de ce chapitre.

NB: la notation : attribut:alias (ex : pays:nom) symbolise un alias (ex: nom) d”attribut (ex: pays) .

Formulation SQL :

On pourra vérifier les requêtes SQL correspondantes aux questions précédentes avec les instances de tables suivantes :

Table « bars »

Table « bieres »

Table « services »

bar_id	bar	pays
1	Bar du Coin	France
2	Corners Pub	USA
3	Cafe der Ecke	Allemagne
4	Cafe des Amis	France

biere_id	biere	couleur	origine
1	Kronenbourg	Blonde	France
2	Guinness	Brune	Irlande
3	Heineken	Blonde	Hollande
4	Newcastle	Rousse	UK
5	Spaten	Blonde	Allemagne
6	Bush	Blonde	USA
7	Kanterbrau	Blonde	France
8	Kronenbourg	Brune	France

bar_id	biere_id	stock
1	1	1000
1	2	250
1	3	50
1	4	10
1	5	10
1	6	10
1	7	40
1	8	60
2	1	100
2	6	1500
3	5	5000

sql : essai.sql

DROP TABLE IF EXISTS bars;
DROP TABLE IF EXISTS bieres;
DROP TABLE IF EXISTS services;

CREATE TABLE bars ( id_bar INTEGER NOT NULL PRIMARY KEY,
                    bar    VARCHAR(20),
                    pays   VARCHAR(20) );

CREATE TABLE bieres ( id_biere  INTEGER NOT NULL PRIMARY KEY,
                      biere     VARCHAR(20),
                      couleur   VARCHAR(10),
                      origine   VARCHAR(20) );

CREATE TABLE services  ( id_bar   INTEGER NOT NULL,
                         id_biere INTEGER NOT NULL,
                         stock    SMALLINT,
                         PRIMARY KEY (id_bar, id_biere),
                         FOREIGN KEY (id_bar)   REFERENCES bars,
                         FOREIGN KEY (id_biere) REFERENCES bieres);

INSERT INTO bars VALUES (1, 'Bar du Coin', 'France');
INSERT INTO bars VALUES (2, 'Corners Pub',  'USA');
INSERT INTO bars VALUES (3, 'Cafe der Ecke','Allemagne');
INSERT INTO bars VALUES (4, 'Cafe des Amis', 'France');

INSERT INTO bieres  VALUES (1, 'Kronenbourg', 'Blonde', 'France');
INSERT INTO bieres  VALUES (2, 'Guinness', 'Brune', 'Irlande');
INSERT INTO bieres  VALUES (3, 'Heineken', 'Blonde', 'Hollande');
INSERT INTO bieres  VALUES (4, 'Newcastle', 'Rousse', 'UK');
INSERT INTO bieres  VALUES (5, 'Spaten', 'Blonde', 'Allemagne');
INSERT INTO bieres  VALUES (6, 'Bush', 'Blonde', 'USA');
INSERT INTO bieres  VALUES (7, 'Kanterbrau', 'Blonde', 'France');
INSERT INTO bieres  VALUES (8, 'Kronenbourg', 'Brune', 'France');

INSERT INTO services VALUES (1,1,1000);
INSERT INTO services VALUES (1,2, 250);
INSERT INTO services VALUES (1,3, 50);
INSERT INTO services VALUES (1,4, 10);
INSERT INTO services VALUES (1,5, 10);
INSERT INTO services VALUES (1,6, 10);
INSERT INTO services VALUES (1,7, 40);
INSERT INTO services VALUES (1,8, 60);
INSERT INTO services VALUES (2,1, 100);
INSERT INTO services VALUES (2,6, 1500);
INSERT INTO services VALUES (3,5, 5000);

Output

Interpréteur

Menu	Action
	Ré-initialiser les sorties
	Faire apparaître le menu d'aide
	Interpréter le programme

Editeur

Menu	Raccouci	Action
	`Ctrl+N`	Initialiser l'éditeur
	`Ctrl+O`	Charger le contenu d'un fichier dans l'éditeur
	`Ctrl+S`	Sauvegarder le contenu de l'éditeur dans un fichier
	`Ctrl+P`	Imprimer le contenu de l'éditeur
	`Ctrl+Z`	Annuler la dernière modification
	`Maj+Ctrl+Z`	Rétablir la modification précedente
	`Ctrl+F`	Chercher une expression dans l'éditeur
	`Maj+Ctrl+F`	Chercher et remplacer une expression par une autre
	`F10`	Ouvrir une documentation du langage

Raccourci	Action
`F1`	Afficher cette aide
`Tab`	Indenter la sélection
`Maj+Tab`	Désindenter la sélection
`Ctrl+A`	Sélectionner le contenu de l'éditeur
`Ctrl+C`	Copier la sélection dans le presse-papier
`Ctrl+V`	Remplacer la sélection par le contenu du presse-papier
`Ctrl+X`	Supprimer la sélection et la copier dans le presse-papier
`Maj+Ctrl+R`	Chercher et remplacer une expression par une autre dans tout l'éditeur

Au Tournoi des six nations

On formulera ici les recherches d’information en calcul relationnel sur le modèle de données du « Tournoi des six nations ».

On pourra vérifier le résultat sur une base de données SQLite en formulant les requêtes SQL.

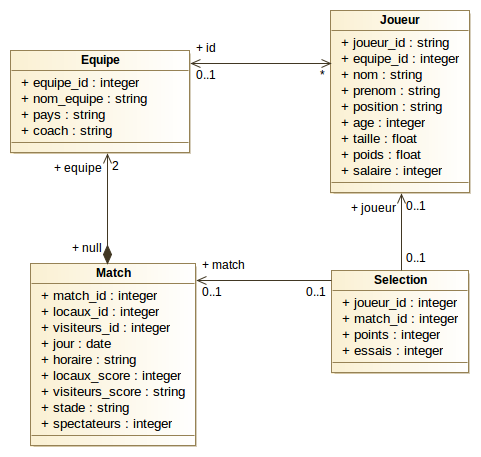
Faire le diagramme de classes correspondant au modèle de données suivant :

une équipe (equipe) a un nom (nom_equipe), fait partie d’une nation (pays) et a un entraîneur (coach)

les joueurs (joueurs) font partie d’une équipe (id_equipe) ont un nom et un prénom (nom,prenom), jouent à un poste précis (position) peuvent être de différentes nationalités (nationalite).

Pour chaque joueur on connaît sa date de naissance, leur taille et leur poids (naissance,taille,poids).

un (match) concerne deux équipes (id_locaux,id_visiteurs), a lieu un jour à un horaire précis (jour,horaire) sur le stade de l’équipe qui accueille (stade)

Chaque match donnera lieu à un score pour l’équipe qui reçoit (locaux_score) et celle qui joue à l’extérieur visiteurs_score).

On notera aussi l’affluence du nombre de spectateurs (spectateurs) le jour du match.

Les matchs donnent lieu à des (selections) de joueurs.

A chaque match (id_match) on associera les joueurs (id_joueur) sélectionnés, le nombre d’essais (essais), de transformations (transformations) et de pénalités qu’ils ont marqués (penalites).

Diagramme de classes

Créer les tables correspondant à ce modèle de données :

Création des tables SQL

CREATE TABLE equipes (
                      id_equipe CHAR(3) PRIMARY KEY,
                      nom_equipe TEXT,
                      pays TEXT,
                      coach TEXT
                     );
CREATE TABLE joueurs (
                      id_joueur INTEGER PRIMARY KEY AUTOINCREMENT,
                      id_equipe  CHAR(3),
                      nom TEXT,
                      prenom TEXT,
                      position TEXT,
                      nationalite TEXT,
                      naissance DATE,
                      taille  FLOAT CHECK (1 < taille and taille < 3) DEFAULT 1.80,
                      poids FLOAT CHECK (50 < poids and poids < 150) DEFAULT 80,
                      FOREIGN KEY(id_equipe) REFERENCES equipes(id_equipe)
                     );
CREATE TABLE matchs (
                     id_match INTEGER PRIMARY KEY  AUTOINCREMENT,
                     id_locaux CHAR(3),
                     id_visiteurs CHAR(3),
                     jour DATE,
                     horaire TIME,
                     locaux_score INTEGER,
                     visiteurs_score INTEGER,
                     stade TEXT,
                     spectateurs INTEGER,
                     FOREIGN KEY(id_locaux) REFERENCES equipes(id_equipe),
                     FOREIGN KEY(id_visiteurs) REFERENCES equipes(id_equipe)
                    );
CREATE TABLE selections (
                         id_joueur INTEGER NOT NULL,
                         id_match INTEGER NOT NULL,
                         essais SMALLINT DEFAULT 0,
                         transformations SMALLINT DEFAULT 0,
                         penalites SMALLINT DEFAULT 0,
                         PRIMARY KEY(id_joueur,id_match),
                         FOREIGN KEY(id_match) REFERENCES matchs(id_match),
                         FOREIGN KEY(id_joueur) REFERENCES joueurs(id_joueur)
                        );

Calcul relationnel :

rechercher les informations suivantes sur le modèle de données en écrivant les requêtes en calcul relationnel et en langage SQL.

nom et prénom des joueurs du tournoi des six nations

Calcul relationnel de domaine :

\(R=\{ (n,p) \; | \; joueurs(-,-,nom:n,prenom:p,-,-,-,-,-) \}\)

Calcul relationnel de n-uplets :

\(R=\{ (j.nom,j.prenom) \; | \; j \in joueurs \}\)

SQL :

SELECT nom,prenom FROM joueurs;

joueurs de l'équipe de France

Calcul relationnel de domaine :

\(R=\{ (id\_j,id\_equipe,n,pr,pos,nat,nai,t,poi) \; |\)

\(\qquad \quad joueurs(id\_joueur:id_j,id\_equipe='FRA',nom:n,prenom:pr,position:pos,\)

\(\qquad \qquad \qquad \qquad nationalite:nat,naissance:nai,taille:t,poids:poi) \}\)

Calcul relationnel de n-uplets :

\(\displaystyle R=\{ j \; | \; j \in joueurs \land j.id\_equipe="FRA" \}\)

SQL :

SELECT * FROM joueurs WHERE id_equipe='FRA';

toutes les combinaisons possibles des joueurs avec les équipes

Calcul relationnel de domaine :

\(R= \{ (id\_eq,eq,p,c,id\_j,id\_e,n,pr,pos,nat,nai,t,poi) \; |\)

\(\qquad \quad equipes(id\_equipe:id\_eq,nom\_equipe:eq,pays:p,coach:c) \land\)

\(\qquad \quad joueurs(id\_joueur:id_j,id\_e:id\_equipe:id_e,nom:n,prenom:pr,position:pos,nationalite:nat,naissance:nai,taille:t,poids:poi) \}\)

Calcul relationnel de n-uplets :

\(R = \{ (e,j) \; | \; e \in equipes \land j \in joueurs \}\)

SQL :

SELECT * FROM equipes, joueurs;
-- ou
SELECT * FROM equipes CROSS JOIN joueurs;

noms du coach et des joueurs du XV de France

Calcul relationnel de domaine :

\(R=\{ nom \; | \; equipes(-,nom\_equipe='XV \; de \; France',-,coach:nom) \lor joueurs(-,id\_equipe='FRA',nom,-,-,-,-,-,-) \}\)

Calcul relationnel de n-uplets :

\(R=\{ nom \; | \; (e.coach:nom, e \in equipes) \land e.nom\_equipe='XV \; de \; France' \lor (j.nom:nom, j \in joueurs \land j.id\_equipe='FRA' ) \}\)

SQL :

(SELECT coach AS nom FROM equipes WHERE nom_equipe='XV de France')
UNION
(SELECT nom FROM  joueurs WHERE id_equipe='FRA');

identifiant des joueurs qui n’ont pas été selectionnés pendant le tournoi des 6 nations

Calcul relationnel de domaine :

\(R=\{ id \; | \; joueurs(id\_joueur:id,-,-,-,-,-,-,-,-) \land \neg selections(id\_joueur:id,-,-,-,-,-,-,-,-) \}\)

Calcul relationnel de n-uplets :

\(R=\{ id \; | (j.id\_joueur:id, j \in joueurs) \land \neg (s.id\_joueur:id, s \in selections) \}\)

SQL :

SELECT id_joueur FROM joueurs
EXCEPT
SELECT id_joueur FROM selections;

identifiant des joueurs qui ont été selectionnés pendant le tournoi des 6 nations

Calcul relationnel de domaine :

\(R=\{ id \; | \; joueurs(id\_joueur:id,-,-,-,-,-,-,-,-) \land selections(id\_joueur:id,-,-,-,-,-,-,-,-) \}\)

Calcul relationnel de n-uplets :

\(R=\{ id \; | (j.id\_joueur:id, j \in joueurs) \land (s.id\_joueur:id, s \in selections) \}\)

SQL :

SELECT id_joueur
FROM joueurs
INTERSECT
SELECT id_joueur
FROM selections;

nom et nationalité des joueurs qui évoluent dans une autre nation que celle de leur pays d'origine.

Calcul relationnel de domaine :

\(R=\{ (nom,nationalite) \; | \; joueurs(-,id\_equipe:id,nom,-,-,nationalite,-,-,-) \land equipes(id\_equipe:id,-,pays,-) \land pays!=nationalite\}\)

Calcul relationnel de n-uplets :

\(R=\{ (j.nom,j.nationalite) \; | \; j \in joueurs \land e \in equipes \land j.id\_equipe=e.id\_equipe \land e.pays!=j.nationalite\}\)

SQL :

SELECT nom,nationalite FROM  joueurs j INNER JOIN equipes e ON (e.id_equipe=j.id_equipe AND e.pays!=j.nationalite);
-- ou
SELECT nom,nationalite FROM joueurs NATURAL JOIN equipes WHERE pays!=nationalite;

nom des joueurs qui ont été sélectionnés pour tous les matchs de leur équipe

Calcul relationnel de domaine :

\(R=\{ nom \; | \; joueurs(id\_joueur,id\_equipe,nom,-,-,-,-,-,-)\)

\(\qquad \qquad \land \; \forall \; match(id\_match,id\_locaux,id\_visiteurs,-,-,-,-,-,-), selections(id\_joueur,id\_match,-,-,-)\)

\(\qquad \qquad \land (id\_equipe=id\_locaux \lor id\_equipe=id\_visiteurs)\}\)

Calcul relationnel de n-uplets :

\(R=\{j.nom \; | \; j \in joueurs \land \; (\forall m \in matchs \; , \; (j.id\_joueur,m.id\_match) \in selections \land\)

\(\qquad \quad (j.id\_equipe=m.id\_locaux \lor j.id\_equipe=m.id\_visiteurs) \}\)

SQL :

L’opérateur n’existe pas en SQL mais peut être exprimé par une double négation (NOT EXISTS)

« Trouver les joueurs tel qu” il n’existe pas de matchs de son equipe pour lesquels il n’ait pas été sélectionné »

SELECT j.nom
FROM joueurs j
WHERE  NOT EXISTS ( SELECT id_match
                    FROM matchs m WHERE j.id_equipe=m.id_locaux OR j.id_equipe=m.id_visiteurs
                    EXCEPT
                    SELECT id_match
                    FROM selections s WHERE j.id_joueur=s.id_joueur);

NB: la notation : attribut:alias (ex : coach:nom) symbolise un alias (ex: nom) d”attribut (ex: coach) .

Formulation SQL :

On pourra vérifier les requêtes SQL correspondantes aux questions précédentes avec les instances de tables suivantes :

Table « equipes »

id_equipe	nom_equipe	pays	coach
FRA	XV de France	France	Novès
ANG	XV de la Rose	Angleterre	Jones
GAL	XV du Poireau	Pays de Galles	Gatland
IRL	XV du Trèfle	Irlande	Schmidt
ECO	XV du Chardon	Ecosse	Cotter
ITA	Azzuri	Italie	Brunel

Table « joueurs »

id_joueur	id_equipe	nom	prenom	position	nationalite	naissance	taille	poids
1	ECO	Laidlaw	Greg	1/2 melee	Ecosse	1985-10-12	1.75	80
2	ECO	Hogg	Stuart	Arriere	Ecosse	1992-06-24	1.8	80
3	ECO	Dunbar	Alex	3/4 centre	Ecosse	1990-04-23	1.91	80
4	ECO	Russell	Finn	1/2 ouverture	Ecosse	1992-09-23	1.83	80
5	ECO	Swinson	Tim	2eme ligne	Angleterre	1987-02-17	1.95	80
6	ECO	Gray	Richie	2eme ligne	Ecosse	1989-08-24	2.06	80
7	IRL	Earls	Keith	3/4 centre	Irlande	1987-10-02	1.8	80
8	IRL	Henderson	Iain	2eme ligne	Irlande du Nord	1992-02-21	1.98	80
9	IRL	Jackson	Paddy	1/2 ouverture	Irlande du Nord	1990-04-05	1.78	80
10	IRL	Stander	Christiaan Johan	3eme ligne centre	Afrique du Sud	1992-01-05	1.89	80
11	IRL	Gilroy	Craig	3/4 aile	Irlande du Nord	1991-03-11	1.83	80
12	IRL	Ringrose	Garry	3/4 centre	Irlande	1995-01-26	1.87	80
13	IRL	Best	Rory	Talonneur	Irlande du Nord	1982-08-15	1.8	80
14	ANG	Te'o	Ben	centre	Nouvelle-Zélande	1987-01-27	1.89	80
15	ANG	Farrell	Owen	3/4 centre	Angleterre	1991-09-24	1.88	80
16	ANG	Daly	Elliot	3/4 centre	Angleterre	1992-10-08	1.84	80
17	ANG	Youngs	Tom	Talonneur	Angleterre	1987-01-28	1.75	80
18	ANG	Cole	Dan	Pilier	Angleterre	1987-05-09	1.91	80
19	FRA	Slimani	Rabah	Pilier	France	1989-10-18	1.78	80
20	FRA	Lopez	Camille	1/2 ouverture	France	1989-04-03	1.75	80
21	FRA	Fickou	Gael	3/4 centre	France	1994-03-29	1.9	80
22	FRA	Spedding	Scott	Arriere	Afrique du Sud	1986-05-04	1.88	80
23	ITA	Gori	Edoardo	1/2 melee	Italie	1990-03-05	1.78	80
24	ITA	Canna	Carlo	1/2 ouverture	Italie	1992-08-25	1.91	80
25	ITA	Parisse	Sergio	3eme ligne	Argentine	1983-09-12	1.96	80
26	GAL	Davies	Jonathan	3/4 centre	Angleterre	1988-04-05	1.86	80
27	GAL	Williams	Liam	3/4 aile	Pays de Galles	1991-04-09	1.88	80
28	GAL	North	George	3/4 aile	Angleterre	1992-04-13	1.92	80
29	GAL	Halfpenny	Leigh	Arriere	Pays de Galles	1988-12-22	1.78	80
30	GAL	Biggar	Dan	1/2 ouverture	Pays de Galles	1989-10-16	1.88	80

Table « matchs »

id_match	id_locaux	id_visiteurs	jour	horaire	locaux_score	visiteurs_score	stade	spectateurs
1	ECO	IRL	2017-02-04	15:25:00	27	22	Murrayfield	67144
2	ANG	FRA	2017-02-04	17:50:00	19	16	Twickenham	81902
3	ITA	GAL	2017-02-05	15:00:00	7	33	Stadio olympico	40986
4	ITA	IRL	2017-02-11	15:25:00	10	63	Stadio olympico	50197
5	GAL	ANG	2017-02-11	17:50:00	16	21	Millennium Stadium	74500
6	FRA	ECO	2017-02-12	16:00:00	22	16	Stade de France	75283
7	ECO	GAL	2017-02-25	15:25:00			Murrayfield
8	IRL	FRA	2017-02-25	17:50:00			Aviva Stadium
9	ANG	ITA	2017-02-26	16:00:00			Twickenham
10	GAL	IRL	2017-03-10	21:05:00			Millennium Stadium
11	ITA	FRA	2017-03-11	14:30:00			Stadio olympico
12	ANG	ECO	2017-03-11	17:00:00			Twickenham
13	ECO	ITA	2017-03-18	13:30:00			Murrayfield
14	FRA	GAL	2017-03-18	15:45:00			Stade de France
15	IRL	ANG	2017-03-18	18:00:00			Aviva Stadium

Table « selections »

id_joueur	id_match	essais	transformations	penalites
2	1	2	0	0
3	1	1	0	0
1	1	0	3	2
7	1	1	0	0
8	1	1	0	0
9	1	1	2	1
14	2	1	0	0
15	2	0	1	3
16	2	0	0	1
19	2	1	0	0
20	2	0	1	3
23	3	1	0	0
24	3	0	1	0
26	3	1	0	0
27	3	1	0	0
28	3	1	0	0
29	3	0	3	4
27	5	1	0	0
29	5	0	1	3
16	5	1	0	0
17	5	1	0	0
15	5	0	1	3
24	4	0	1	1
7	4	2	0	0
10	4	3	0	0
11	4	3	0	0
12	4	1	0	0
9	4	0	9	0
21	6	1	0	0
20	6	0	1	5
2	6	1	0	0
5	6	1	0	0
4	6	0	0	2
20	8	0	0	0
20	11	0	0	0
20	14	0	0	0

sql : sixnations.sql

DROP TABLE IF EXISTS equipes;
DROP TABLE IF EXISTS joueurs;
DROP TABLE IF EXISTS matchs;
DROP TABLE IF EXISTS selections;

CREATE TABLE equipes (
                      id_equipe CHAR(3) PRIMARY KEY,
                      nom_equipe TEXT,
                      pays TEXT,
                      coach TEXT
                     );
CREATE TABLE joueurs (
                      id_joueur INTEGER PRIMARY KEY AUTOINCREMENT,
                      id_equipe  CHAR(3),
                      nom TEXT,
                      prenom TEXT,
                      position TEXT,
                      nationalite TEXT,
                      naissance DATE,
                      taille  FLOAT CHECK (1 < taille and taille < 3) DEFAULT 1.80,
                      poids FLOAT CHECK (50 < poids and poids < 150) DEFAULT 80,
                      FOREIGN KEY(id_equipe) REFERENCES equipes(id_equipe)
                     );
CREATE TABLE matchs (
                     id_match INTEGER PRIMARY KEY  AUTOINCREMENT,
                     id_locaux CHAR(3),
                     id_visiteurs CHAR(3),
                     jour DATE,
                     horaire TIME,
                     locaux_score INTEGER,
                     visiteurs_score INTEGER,
                     stade TEXT,
                     spectateurs INTEGER,
                     FOREIGN KEY(id_locaux) REFERENCES equipes(id_equipe),
                     FOREIGN KEY(id_visiteurs) REFERENCES equipes(id_equipe)
                    );
CREATE TABLE selections (
                         id_joueur INTEGER NOT NULL,
                         id_match INTEGER NOT NULL,
                         essais SMALLINT DEFAULT 0,
                         transformations SMALLINT DEFAULT 0,
                         penalites SMALLINT DEFAULT 0,
                         PRIMARY KEY(id_joueur,id_match),
                         FOREIGN KEY(id_match) REFERENCES matchs(id_match),
                         FOREIGN KEY(id_joueur) REFERENCES joueurs(id_joueur)
                        );

-- equipes
INSERT INTO equipes (id_equipe,nom_equipe,pays,coach) VALUES ('FRA','XV de France','France','Noves');
INSERT INTO equipes (id_equipe,nom_equipe,pays,coach) VALUES ('ANG','XV de la Rose','Angleterre','Jones');
INSERT INTO equipes (id_equipe,nom_equipe,pays,coach) VALUES ('GAL','XV du Poireau','Pays de Galles','Howley');
INSERT INTO equipes (id_equipe,nom_equipe,pays,coach) VALUES ('IRL','XV du Trèfle','Irlande','Schmidt');
INSERT INTO equipes (id_equipe,nom_equipe,pays,coach) VALUES ('ECO','XV du Chardon','Ecosse','Cotter');
INSERT INTO equipes (id_equipe,nom_equipe,pays,coach) VALUES ('ITA','Azzuri','Italie','O''shea');

-- matchs : journee du 04-05 février
INSERT INTO matchs (id_locaux,id_visiteurs,jour,horaire,locaux_score,visiteurs_score,stade, spectateurs)
       select e1.id_equipe,e2.id_equipe,'2017-02-04','15:25:00',27,22,'Murrayfield',67144 from equipes e1, equipes e2 where e1.pays='Ecosse' AND e2.pays='Irlande';
INSERT INTO matchs (id_locaux,id_visiteurs,jour,horaire,locaux_score,visiteurs_score,stade, spectateurs)
       select e1.id_equipe,e2.id_equipe,'2017-02-04','17:50:00',19,16,'Twickenham',81902 from equipes e1, equipes e2 where e1.pays='Angleterre' AND e2.pays='France';
INSERT INTO matchs (id_locaux,id_visiteurs,jour,horaire,locaux_score,visiteurs_score,stade, spectateurs)
       select e1.id_equipe,e2.id_equipe,'2017-02-05','15:00:00',7,33,'Stadio olympico',40986  from equipes e1, equipes e2 where e1.pays='Italie' AND e2.pays='Pays de Galles';

-- matchs : journee du 11-12 février
INSERT INTO matchs (id_locaux,id_visiteurs,jour,horaire,locaux_score,visiteurs_score,stade, spectateurs)
       select e1.id_equipe,e2.id_equipe,'2017-02-11','15:25:00',10,63,'Stadio olympico',50197 from equipes e1, equipes e2 where e1.pays='Italie' AND e2.pays='Irlande';
INSERT INTO matchs (id_locaux,id_visiteurs,jour,horaire,locaux_score,visiteurs_score,stade, spectateurs)
       select e1.id_equipe,e2.id_equipe,'2017-02-11','17:50:00',16,21,'Millennium Stadium',74500 from equipes e1, equipes e2 where e1.pays='Pays de Galles' AND e2.pays='Angleterre';
INSERT INTO matchs (id_locaux,id_visiteurs,jour,horaire,locaux_score,visiteurs_score,stade, spectateurs)
       select e1.id_equipe,e2.id_equipe,'2017-02-12','16:00:00',22,16,'Stade de France',75283 from equipes e1, equipes e2 where e1.pays='France' AND e2.pays='Ecosse';

-- matchs : journee du 25-26 février
INSERT INTO matchs (id_locaux,id_visiteurs,jour,horaire,locaux_score,visiteurs_score,stade, spectateurs)
       select e1.id_equipe,e2.id_equipe,'2017-02-25','15:25:00',NULL,NULL,'Murrayfield',NULL from equipes e1, equipes e2 where e1.pays='Ecosse' AND e2.pays='Pays de Galles';
INSERT INTO matchs (id_locaux,id_visiteurs,jour,horaire,locaux_score,visiteurs_score,stade, spectateurs)
       select e1.id_equipe,e2.id_equipe,'2017-02-25','17:50:00',NULL,NULL,'Aviva Stadium',NULL from equipes e1, equipes e2 where e1.pays='Irlande' AND e2.pays='France';
INSERT INTO matchs (id_locaux,id_visiteurs,jour,horaire,locaux_score,visiteurs_score,stade, spectateurs)
       select e1.id_equipe,e2.id_equipe,'2017-02-26','16:00:00',NULL,NULL,'Twickenham',NULL from equipes e1, equipes e2 where e1.pays='Angleterre' AND e2.pays='Italie';

-- matchs : journee du 10-11 mars
INSERT INTO matchs (id_locaux,id_visiteurs,jour,horaire,locaux_score,visiteurs_score,stade, spectateurs)
       select e1.id_equipe,e2.id_equipe,'2017-03-10','21:05:00',NULL,NULL,'Millennium Stadium',NULL from equipes e1, equipes e2 where e1.pays='Pays de Galles' AND e2.pays='Irlande';
INSERT INTO matchs (id_locaux,id_visiteurs,jour,horaire,locaux_score,visiteurs_score,stade, spectateurs)
       select e1.id_equipe,e2.id_equipe,'2017-03-11','14:30:00',NULL,NULL,'Stadio olympico',NULL from equipes e1, equipes e2 where e1.pays='Italie' AND e2.pays='France';
INSERT INTO matchs (id_locaux,id_visiteurs,jour,horaire,locaux_score,visiteurs_score,stade, spectateurs)
       select e1.id_equipe,e2.id_equipe,'2017-03-11','17:00:00',NULL,NULL,'Twickenham',NULL from equipes e1, equipes e2 where e1.pays='Angleterre' AND e2.pays='Ecosse';

-- matchs : journee du 18 mars
INSERT INTO matchs (id_locaux,id_visiteurs,jour,horaire,locaux_score,visiteurs_score,stade, spectateurs)
       select e1.id_equipe,e2.id_equipe,'2017-03-18','13:30:00',NULL,NULL,'Murrayfield',NULL from equipes e1, equipes e2 where e1.pays='Ecosse' AND e2.pays='Italie';
INSERT INTO matchs (id_locaux,id_visiteurs,jour,horaire,locaux_score,visiteurs_score,stade, spectateurs)
       select e1.id_equipe,e2.id_equipe,'2017-03-18','15:45:00',NULL,NULL,'Stade de France',NULL from equipes e1, equipes e2 where e1.pays='France' AND e2.pays='Pays de Galles';
INSERT INTO matchs (id_locaux,id_visiteurs,jour,horaire,locaux_score,visiteurs_score,stade, spectateurs)
       select e1.id_equipe,e2.id_equipe,'2017-03-18','18:00:00',NULL,NULL,'Aviva Stadium',NULL from equipes e1, equipes e2 where e1.pays='Irlande' AND e2.pays='Angleterre';

-- joueurs:  Ecosse
INSERT INTO joueurs (id_equipe, nom, prenom, position,nationalite,naissance,taille)
VALUES ('ECO','Laidlaw','Greg','1/2 melee','Ecosse','1985-10-12',1.75);
INSERT INTO joueurs (id_equipe, nom, prenom, position,nationalite,naissance,taille)
VALUES ('ECO','Hogg','Stuart','Arriere','Ecosse','1992-06-24',1.80);
INSERT INTO joueurs (id_equipe, nom, prenom, position,nationalite,naissance,taille)
VALUES ('ECO','Dunbar','Alex','3/4 centre','Ecosse','1990-04-23',1.91);
INSERT INTO joueurs (id_equipe, nom, prenom, position,nationalite,naissance,taille)
VALUES ('ECO','Russell','Finn','1/2 ouverture','Ecosse','1992-09-23',1.83);
INSERT INTO joueurs (id_equipe, nom, prenom, position,nationalite,naissance,taille)
VALUES ('ECO','Swinson','Tim','2eme ligne','Angleterre','1987-02-17',1.95);
INSERT INTO joueurs (id_equipe, nom, prenom, position,nationalite,naissance,taille)
VALUES ('ECO','Gray','Richie','2eme ligne','Ecosse','1989-08-24',2.06);

-- joueurs:  Irlande
INSERT INTO joueurs (id_equipe, nom, prenom, position,nationalite,naissance,taille)
VALUES ('IRL','Earls','Keith','3/4 centre','Irlande','1987-10-02',1.80);
INSERT INTO joueurs (id_equipe, nom, prenom, position,nationalite,naissance,taille)
VALUES ('IRL','Henderson','Iain','2eme ligne','Irlande du Nord','1992-02-21',1.98);
INSERT INTO joueurs (id_equipe, nom, prenom, position,nationalite,naissance,taille)
VALUES ('IRL','Jackson','Paddy','1/2 ouverture','Irlande du Nord','1990-04-05',1.78);
INSERT INTO joueurs (id_equipe, nom, prenom, position,nationalite,naissance,taille)
VALUES ('IRL','Stander','Christiaan Johan','3eme ligne centre','Afrique du Sud','1992-01-05',1.89);
INSERT INTO joueurs (id_equipe, nom, prenom, position,nationalite,naissance,taille)
VALUES ('IRL','Gilroy','Craig','3/4 aile','Irlande du Nord','1991-03-11',1.83);
INSERT INTO joueurs (id_equipe, nom, prenom, position,nationalite,naissance,taille)
VALUES ('IRL','Ringrose','Garry','3/4 centre','Irlande','1995-01-26',1.87);
INSERT INTO joueurs (id_equipe, nom, prenom, position,nationalite,naissance,taille)
VALUES ('IRL','Best','Rory','Talonneur','Irlande du Nord','1982-08-15',1.80);

-- joueurs:  Angleterre
INSERT INTO joueurs (id_equipe, nom, prenom, position,nationalite,naissance,taille)
VALUES ('ANG','Te''o','Ben','centre','Nouvelle-Zélande','1987-01-27',1.89);
INSERT INTO joueurs (id_equipe, nom, prenom, position,nationalite,naissance,taille)
VALUES ('ANG','Farrell','Owen','3/4 centre','Angleterre','1991-09-24',1.88);
INSERT INTO joueurs (id_equipe, nom, prenom, position,nationalite,naissance,taille)
VALUES ('ANG','Daly','Elliot','3/4 centre','Angleterre','1992-10-08',1.84);
INSERT INTO joueurs (id_equipe, nom, prenom, position,nationalite,naissance,taille)
VALUES ('ANG','Youngs','Tom','Talonneur','Angleterre','1987-01-28',1.75);
INSERT INTO joueurs (id_equipe, nom, prenom, position,nationalite,naissance,taille)
VALUES ('ANG','Cole','Dan','Pilier','Angleterre','1987-05-09',1.91);

-- joueurs:  France
INSERT INTO joueurs (id_equipe, nom, prenom, position,nationalite,naissance,taille)
VALUES ('FRA','Slimani','Rabah','Pilier','France','1989-10-18',1.78);
INSERT INTO joueurs (id_equipe, nom, prenom, position,nationalite,naissance,taille)
VALUES ('FRA','Lopez','Camille','1/2 ouverture','France','1989-04-03',1.75);
INSERT INTO joueurs (id_equipe, nom, prenom, position,nationalite,naissance,taille)
VALUES ('FRA','Fickou','Gael','3/4 centre','France','1994-03-29',1.90);
INSERT INTO joueurs (id_equipe, nom, prenom, position,nationalite,naissance,taille)
VALUES ('FRA','Spedding','Scott','Arriere','Afrique du Sud','1986-05-04',1.88);

-- joueurs:  Italie
INSERT INTO joueurs (id_equipe, nom, prenom, position,nationalite,naissance,taille)
VALUES ('ITA','Gori','Edoardo','1/2 melee','Italie','1990-03-05',1.78);
INSERT INTO joueurs (id_equipe, nom, prenom, position,nationalite,naissance,taille)
VALUES ('ITA','Canna','Carlo','1/2 ouverture','Italie','1992-08-25',1.91);
INSERT INTO joueurs (id_equipe, nom, prenom, position,nationalite,naissance,taille)
VALUES ('ITA','Parisse','Sergio','3eme ligne','Argentine','1983-09-12',1.96);

-- joueurs:  Pays de Galles
INSERT INTO joueurs (id_equipe, nom, prenom, position,nationalite,naissance,taille)
VALUES ('GAL','Davies','Jonathan','3/4 centre','Angleterre','1988-04-05',1.86);
INSERT INTO joueurs (id_equipe, nom, prenom, position,nationalite,naissance,taille)
VALUES ('GAL','Williams','Liam','3/4 aile','Pays de Galles','1991-04-09',1.88);
INSERT INTO joueurs (id_equipe, nom, prenom, position,nationalite,naissance,taille)
VALUES ('GAL','North','George','3/4 aile','Angleterre','1992-04-13',1.92);
INSERT INTO joueurs (id_equipe, nom, prenom, position,nationalite,naissance,taille)
VALUES ('GAL','Halfpenny','Leigh','Arriere','Pays de Galles','1988-12-22',1.78);
INSERT INTO joueurs (id_equipe, nom, prenom, position,nationalite,naissance,taille)
VALUES ('GAL','Biggar','Dan','1/2 ouverture','Pays de Galles','1989-10-16',1.88);

/*
INSERT INTO joueurs (id_equipe, nom, prenom, position) VALUES ('FRA','Poireau','Jefferson','Pilier');
INSERT INTO joueurs (id_equipe, nom, prenom, position) VALUES ('FRA','Bonfils','Remi','Talonneur');
INSERT INTO joueurs (id_equipe, nom, prenom, position) VALUES ('FRA','Medard','Maxime','Arriere');

IINSERT INTO joueurs (id_equipe, nom, prenom, position) VALUES ('GAL','Biggar','Daniel','Ouverture');
INSERT INTO joueurs (id_equipe, nom, prenom, position) VALUES ('IRL','O Brian','Sean','3eme ligne');
INSERT INTO joueurs (id_equipe, nom, prenom, position) VALUES ('ITA','Sarto','Leonardo','3/4');
*/

-- selections:  Ecosse-Irlande
INSERT INTO  selections (id_joueur,id_match,essais) SELECT id_joueur,id_match,2
FROM matchs,joueurs WHERE nom='Hogg' AND jour='2017-02-04' AND id_locaux='ECO';
INSERT INTO  selections (id_joueur,id_match,essais) SELECT id_joueur,id_match,1
FROM matchs,joueurs WHERE nom='Dunbar' AND jour='2017-02-04' AND id_locaux='ECO';
INSERT INTO  selections (id_joueur,id_match,transformations,penalites) SELECT id_joueur,id_match,3,2
FROM matchs,joueurs WHERE nom='Laidlaw' AND jour='2017-02-04' AND id_locaux='ECO';

INSERT INTO  selections (id_joueur,id_match,essais) SELECT id_joueur,id_match,1
FROM matchs,joueurs WHERE nom='Earls' AND jour='2017-02-04' AND id_visiteurs='IRL';
INSERT INTO  selections (id_joueur,id_match,essais) SELECT id_joueur,id_match,1
FROM matchs,joueurs WHERE nom='Henderson' AND jour='2017-02-04' AND id_visiteurs='IRL';
INSERT INTO  selections (id_joueur,id_match,essais,transformations,penalites) SELECT id_joueur,id_match,1,2,1
FROM matchs,joueurs WHERE nom='Jackson' AND jour='2017-02-04' AND id_visiteurs='IRL';

-- selections:  Angleterre-France
INSERT INTO  selections (id_joueur,id_match,essais) SELECT id_joueur,id_match,1
FROM matchs,joueurs WHERE nom='Te''o' AND jour='2017-02-04' AND id_locaux='ANG';
INSERT INTO  selections (id_joueur,id_match,transformations,penalites) SELECT id_joueur,id_match,1,3
FROM matchs,joueurs WHERE nom='Farrell' AND jour='2017-02-04' AND id_locaux='ANG';
INSERT INTO  selections (id_joueur,id_match,penalites) SELECT id_joueur,id_match,1
FROM matchs,joueurs WHERE nom='Daly' AND jour='2017-02-04' AND id_locaux='ANG';

INSERT INTO  selections (id_joueur,id_match,essais) SELECT id_joueur,id_match,1
FROM matchs,joueurs WHERE nom='Slimani' AND jour='2017-02-04' AND  id_visiteurs='FRA';
INSERT INTO  selections (id_joueur,id_match,transformations,penalites) SELECT id_joueur,id_match,1,3
FROM matchs,joueurs WHERE nom='Lopez' AND jour='2017-02-04' AND id_visiteurs='FRA';
-- selections:  Italie-Pays de Galles
INSERT INTO  selections (id_joueur,id_match,essais) SELECT id_joueur,id_match,1
FROM matchs,joueurs WHERE nom='Gori' AND jour='2017-02-05' AND id_locaux='ITA';
INSERT INTO  selections (id_joueur,id_match,transformations) SELECT id_joueur,id_match,1
FROM matchs,joueurs WHERE nom='Canna' AND jour='2017-02-05' AND id_locaux='ITA';

INSERT INTO  selections (id_joueur,id_match,essais) SELECT id_joueur,id_match,1
FROM matchs,joueurs WHERE nom='Davies' AND jour='2017-02-05' AND id_visiteurs='GAL';
INSERT INTO  selections (id_joueur,id_match,essais) SELECT id_joueur,id_match,1
FROM matchs,joueurs WHERE nom='Williams' AND jour='2017-02-05' AND id_visiteurs='GAL';
INSERT INTO  selections (id_joueur,id_match,essais) SELECT id_joueur,id_match,1
FROM matchs,joueurs WHERE nom='North' AND jour='2017-02-05' AND id_visiteurs='GAL';
INSERT INTO  selections (id_joueur,id_match,transformations,penalites) SELECT id_joueur,id_match,3,4
FROM matchs,joueurs WHERE nom='Halfpenny' AND jour='2017-02-05' AND id_visiteurs='GAL';

-- selections:  Pays de Galles-Angleterre
INSERT INTO  selections (id_joueur,id_match,essais) SELECT id_joueur,id_match,1
FROM matchs,joueurs WHERE nom='Williams' AND jour='2017-02-11' AND id_locaux='GAL';
INSERT INTO  selections (id_joueur,id_match,transformations,penalites) SELECT id_joueur,id_match,1,3
FROM matchs,joueurs WHERE nom='Halfpenny' AND jour='2017-02-11' AND id_locaux='GAL';

INSERT INTO  selections (id_joueur,id_match,essais) SELECT id_joueur,id_match,1
FROM matchs,joueurs WHERE nom='Daly' AND jour='2017-02-11' AND id_visiteurs='ANG';
INSERT INTO  selections (id_joueur,id_match,essais) SELECT id_joueur,id_match,1
FROM matchs,joueurs WHERE nom='Youngs' AND jour='2017-02-11' AND id_visiteurs='ANG';
INSERT INTO  selections (id_joueur,id_match,transformations,penalites) SELECT id_joueur,id_match,1,3
FROM matchs,joueurs WHERE nom='Farrell' AND jour='2017-02-11' AND id_visiteurs='ANG';

-- selections:  Pays de Italie-Irlande
INSERT INTO  selections (id_joueur,id_match,transformations,penalites) SELECT id_joueur,id_match,1,1
FROM matchs,joueurs WHERE nom='Canna' AND jour='2017-02-11' AND id_locaux='ITA';

INSERT INTO  selections (id_joueur,id_match,essais) SELECT id_joueur,id_match,2
FROM matchs,joueurs WHERE nom='Earls' AND jour='2017-02-11' AND id_visiteurs='IRL';
INSERT INTO  selections (id_joueur,id_match,essais) SELECT id_joueur,id_match,3
FROM matchs,joueurs WHERE nom='Stander' AND jour='2017-02-11' AND id_visiteurs='IRL';
INSERT INTO  selections (id_joueur,id_match,essais) SELECT id_joueur,id_match,3
FROM matchs,joueurs WHERE nom='Gilroy' AND jour='2017-02-11' AND id_visiteurs='IRL';
INSERT INTO  selections (id_joueur,id_match,essais) SELECT id_joueur,id_match,1
FROM matchs,joueurs WHERE nom='Ringrose' AND jour='2017-02-11' AND id_visiteurs='IRL';
INSERT INTO  selections (id_joueur,id_match,transformations) SELECT id_joueur,id_match,9
FROM matchs,joueurs WHERE nom='Jackson' AND jour='2017-02-11' AND id_visiteurs='IRL';

-- selections:  France-Ecosse
INSERT INTO  selections (id_joueur,id_match,essais) SELECT id_joueur,id_match,1
FROM matchs,joueurs WHERE nom='Fickou' AND jour='2017-02-12' AND id_locaux='FRA';
INSERT INTO  selections (id_joueur,id_match,transformations,penalites) SELECT id_joueur,id_match,1,5
FROM matchs,joueurs WHERE nom='Lopez' AND jour='2017-02-12' AND id_locaux='FRA';

INSERT INTO  selections (id_joueur,id_match,essais) SELECT id_joueur,id_match,1
FROM matchs,joueurs WHERE nom='Hogg' AND jour='2017-02-12' AND id_visiteurs='ECO';
INSERT INTO  selections (id_joueur,id_match,essais) SELECT id_joueur,id_match,1
FROM matchs,joueurs WHERE nom='Swinson' AND jour='2017-02-12' AND id_visiteurs='ECO';
INSERT INTO  selections (id_joueur,id_match,penalites) SELECT id_joueur,id_match,2
FROM matchs,joueurs WHERE nom='Russell' AND jour='2017-02-12' AND id_visiteurs='ECO';

-- selections:  Irlande-France
INSERT INTO  selections (id_joueur,id_match) SELECT id_joueur,id_match
FROM matchs,joueurs WHERE nom='Lopez' AND jour='2017-02-25' AND id_visiteurs='FRA';
-- selections:  Italie-France
INSERT INTO  selections (id_joueur,id_match) SELECT id_joueur,id_match
FROM matchs,joueurs WHERE nom='Lopez' AND jour='2017-03-11' AND id_visiteurs='FRA';
-- selections:  France-Galles
INSERT INTO  selections (id_joueur,id_match) SELECT id_joueur,id_match
FROM matchs,joueurs WHERE nom='Lopez' AND jour='2017-03-18' AND id_locaux='FRA';

Output

Interpréteur

Menu	Action
	Ré-initialiser les sorties
	Faire apparaître le menu d'aide
	Interpréter le programme

Editeur

Menu	Raccouci	Action
	`Ctrl+N`	Initialiser l'éditeur
	`Ctrl+O`	Charger le contenu d'un fichier dans l'éditeur
	`Ctrl+S`	Sauvegarder le contenu de l'éditeur dans un fichier
	`Ctrl+P`	Imprimer le contenu de l'éditeur
	`Ctrl+Z`	Annuler la dernière modification
	`Maj+Ctrl+Z`	Rétablir la modification précedente
	`Ctrl+F`	Chercher une expression dans l'éditeur
	`Maj+Ctrl+F`	Chercher et remplacer une expression par une autre
	`F10`	Ouvrir une documentation du langage

Raccourci	Action
`F1`	Afficher cette aide
`Tab`	Indenter la sélection
`Maj+Tab`	Désindenter la sélection
`Ctrl+A`	Sélectionner le contenu de l'éditeur
`Ctrl+C`	Copier la sélection dans le presse-papier
`Ctrl+V`	Remplacer la sélection par le contenu du presse-papier
`Ctrl+X`	Supprimer la sélection et la copier dans le presse-papier
`Maj+Ctrl+R`	Chercher et remplacer une expression par une autre dans tout l'éditeur

Fichier de rejeu Close

Indication Close

A propos de... Close

Commentaire Close

Systèmes d'Information

Archives

Aide

En-tête

Pied de page

Calcul relationnel

Définition

Aux pays des bières

Interpréteur

Editeur

Au Tournoi des six nations

Interpréteur

Editeur