Fichier de rejeu Close
Indication Close
A propos de... Close
Commentaire Close
Systèmes d'Information
- Notions mathématiques
- Calcul relationnel
- Algèbre relationnelle
- Langage de requêtes
- Arbre de requêtes
- Exercices
- Introduction
- Commandes de bases
- Langage de définition de données (LDD)
- Langage de manipulation de données (LMD)
- Types de données
- Exercice
- Dépendances fonctionnelles
- Décomposition de relations
- Inférence logique
- Normalisation
- Aux pays des bières
- Modélisation
- Exercices
© Your Copyright
Aide
Fonction
Nous présentons ici la définition d’une fonction entre deux ensembles sous forme de :
- définition mathématique
- cardinalité d’une relation fonctionnelle
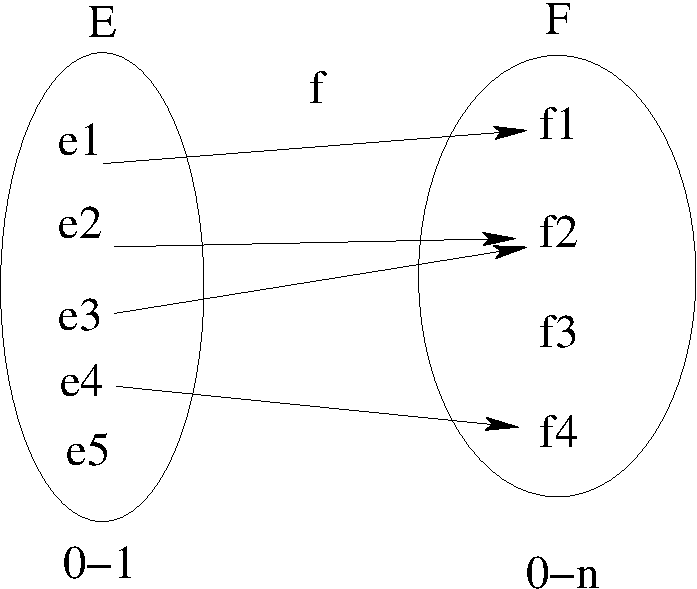
- diagramme sagittal
- modèle Entité-Association
- modélisation UML
puis nous illustrons cette notion mathématique sur un exemple simple d’un ensemble d’employés et de sociétés.
Une relation binaire \(R\) est une fonction si et seulement si :
- \(\forall (x,y,y') \in( E \times F \times F) \; , \; xRy \land xRy' \Rightarrow y=y'\)
Autrement dit, une relation fonctionnelle \(f\) d’un ensemble \(E\) vers un ensemble \(F\) notée :
\[f : E \rightarrow F\]\[ x \mapsto f(x)\]est une relation binaire de \(E\) vers \(F\) pour laquelle :
- les éléments de l’ensemble \(E\) peuvent être associés au plus à un élément de \(F\)
- \((0-1)\) : un élément de \(E\) est en relation avec au plus un élément de \(F\).
- \((0-n)\) : les éléments de \(F\) peuvent être (ou pas) en relation avec un ou plusieurs éléments de \(E\).
Le diagramme sagittal ci-dessous représente un exemple de relation fonctionnelle.
Les cardinalités d’une fonction sont representées sous les ensembles \(E,F\).
La répresentation d’une fonction dans un modèle Entité-Assocation se représente avec le formalisme ci-dessous :
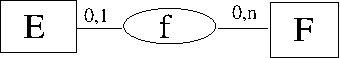
On remarquera que dans le formalisme E-A les notations sont très similaires :
- le positionnement des cardinalités est du même côté (des entités au lieu des ensembles)
- la notation des cardinalités (\(0,1\) et \(0,n\)) correspond aux notations (\(0-1\) et \(0-n\))
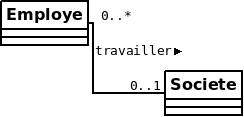
La répresentation d’une fonction dans un modèle UML se représente avec le formalisme ci-dessous :
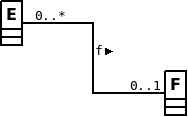
On remarquera que dans le formalisme UML les notations sont différentes :
le positionnement des cardinalités est inversé par rapport au diagramme sagittal et au modèle E-A.
la notation UML (\(0..1\)) correspond à la notation (\(0-1\)) :
- un élément de \(E\) peut être (\(0-\)) en relation avec un seul (\(-1\)) élément de \(F\).
la notation UML (\(0..*\)) correspond à la notation (\(0-n\)) :
- un élément de \(F\) peut, ou pas (\(0..\)), être en relation avec un ou plusieurs (\(..*\)) éléments de \(E\).
En UML la notation (\(*\)) est une autre représentation possible de la cardinalité (\(0..*\))
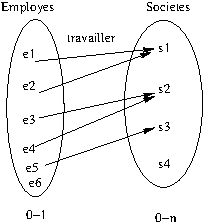
On veut modéliser un système d’information qui permettrait de gérer des employés dans des sociétés.
Dans cette relation fonctionnelle on veut exprimer les contraintes suivantes sur les employés et les sociétés :
- un employé peut travailler au plus dans une seule société.
- une société peut avoir un, plusieurs ou aucun employés
- \((0-1)\) : un
Employépeut travailler au plus dans uneSociété. - \((0-n)\) : les
Sociétépeuvent avoir un, plusieurs ou aucunEmployé.
Les contraintes de la relation Employé-Société sont celles d’une relation fonctionnelle que l’on peut illustrer avec l’exemple de
diagramme sagittal ci-dessous :
La répresentation de la relation fonctionnelle Employé-Société dans le formalisme Entité-Assocation :
La répresentation de la relation fonctionnelle Employé-Société dans le formalisme UML :
