Fichier de rejeu Close

Indication Close

A propos de... Close

Commentaire Close

Systèmes d'Information

Liste des projets

Index

Aide

Menu	Contenu
	Sommaire, Téléchargements
	Aide sur les outils

Chevron	Action
	Aller en haut de la page courante
	Aller en bas de la page courante
	Passer à la page précédente
	Passer à la page suivante

Généralités

Concerts

Répondre aux questions suivantes :

QCM généralités

Répondre au QCM ci-dessous.

Votre réponse :

3/3 ensembles, logique, SQL

polynômes du second degré

La fonction \(f : x \rightarrow x^2\), définie sur \(f : \mathbb{R} \rightarrow \mathbb{R}\), est :
1. aucune des trois autres propositions
2. seulement surjective
3. seulement injective
4. bijective
cardinalité

Parmi ces expressions une seule est correcte, laquelle ? ?
1. \(card(\cup(E_1,E_2)) = card(E_1) + card(E_2) - card(\cap(E_1,E_2))\)
2. \(card(\cup(E_1,E_2)) = card(E_1) + card(E_2) + card(\cap(E_1,E_2))\)
3. \(card(\setminus(E_1,E_2)) = card(E_1) - card(E_2) + card(\cap(E_1,E_2))\)
4. \(card(\setminus(E_1,E_2)) = card(E_1) - card(E_2) - card(\cap(E_1,E_2))\)

Opérateurs

Combien y a t’il d’opérateurs fondamentaux (de base) de l’algèbre relationnelle

nombre d’opérateurs de base : 5
nombre d’opérateurs de base : 3
nombre d’opérateurs de base : 8
nombre d’opérateurs de base : 10

/0100/:	Le nombre d’opérateurs et son nombre de fibonacci sont identiques
/0010/:	Le nombre d’opérateurs et son nombre de fibonacci sont identiques
/0001/:	Le nombre d’opérateurs et son nombre de fibonacci sont identiques

gagné

QCM	Radio	Checkbox	Total
Nombre de questions
Réponses non enregistrées
Réponses enregistrées
Taux d'enregistrement
Réponses enregistrées non validées
Réponses enregistrées validées
Taux de réussite partiel
Taux de réussite total

Une solution possible :

Voir directement les réponses fournies par le QCM lui-même.

Logique : implication

Traduisez en propositions et implication la phrase suivante :

« Si l’accusé est coupable il n’a pas d’alibi. »

Faites la table de vérité correspondant et interpréter tous les cas.

Votre réponse :

Texte : inputlines889.txt

Zone de saisie de texte

Clavier	Action
`F1`	Afficher une aide technique
`F2`	Afficher une aide pédagogique
`Ctrl-A`	Tout sélectionner
`Ctrl-C`	Copier la sélection dans le presse-papier
`Ctrl-V`	Copier le presse-papier dans la sélection
`Ctrl-X`	Couper la sélection et la copier dans le presse-papier
`Ctrl-Z`	Annuler la modification
`Maj-Ctrl-Z`	Rétablir la modification

Menu	Action
	Ré-initialiser les sorties
	Faire apparaître le menu d'aide
	Valider la zone de saisie
	Initialiser la zone de saisie
	Charger le contenu d'un fichier dans la zone de saisie
	Sauvegarder le contenu de la zone de saisie dans un fichier
	Imprimer le contenu de la zone de saisie

Une solution possible :

de la phrase : « Si l’accusé est coupable il n’a pas d’alibi. »

nous pouvons établir les propositions suivantes :

\(P\) : « l’accusé est coupable »

\(Q\) : « il n’a pas d’alibi »

Et donc l’implication : SI \(P\) ALORS \(Q\)

En représentant la table de vérité de l’implication :

Implication

P Q P => Q

0 0 1

0 1 1

1 0 0

1 1 1

Implication
P	Q	P => Q
0	0	1
0	1	1
1	0	0
1	1	1

On peut interpréter les différents cas :

\(P,Q\) sont toutes deux fausses : l’accusé n’est pas coupable et il a un alibi (ç’est classique !)

\(P\) fausse, \(Q\) vraie : l’accusé n’est pas coupable et il n’a pas d’alibi (ça arrive !)

\(P\) vraie, \(Q\) fausse : l’accusé est coupable et il a un alibi (ce n’est pas possible, l’alibi ment !)

\(P\) vraie, \(Q\) vraie : l’accusé est coupable et il n’a pas d’alibi (c’est normal !)

Ensembles et programmation

Soit le code python suivant :

for i in [2,3,4] :
    for j in [1,2,3] :
        print (i**j)

Représentez en extension l’ensemble des résultats affichés par ce code.

Remarque : en python i**j signifie i à la puissance j ( \(i^j\))

Votre réponse :

Texte : inputlines893.txt

Zone de saisie de texte

Clavier	Action
`F1`	Afficher une aide technique
`F2`	Afficher une aide pédagogique
`Ctrl-A`	Tout sélectionner
`Ctrl-C`	Copier la sélection dans le presse-papier
`Ctrl-V`	Copier le presse-papier dans la sélection
`Ctrl-X`	Couper la sélection et la copier dans le presse-papier
`Ctrl-Z`	Annuler la modification
`Maj-Ctrl-Z`	Rétablir la modification

Menu	Action
	Ré-initialiser les sorties
	Faire apparaître le menu d'aide
	Valider la zone de saisie
	Initialiser la zone de saisie
	Charger le contenu d'un fichier dans la zone de saisie
	Sauvegarder le contenu de la zone de saisie dans un fichier
	Imprimer le contenu de la zone de saisie

Une solution possible :

\(E=\{2,4,8,3,9,27,4,16,64 \}\)

A partir du modèle de données :

concerts (groupe, style)

musiciens (nom, groupe)

répondre aux questions suivantes

de l'algèbre relationnelle au langage naturel

Exprimer sous forme de question, en une simple phrase en langage naturel, l’expression algébrique suivante :

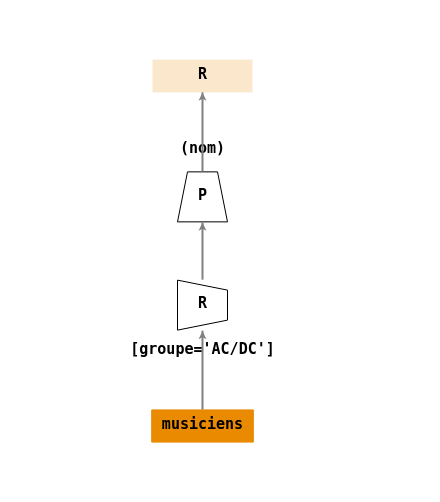
\(R=\Pi_{nom}(\sigma_{[groupe='AC/DC']}(musiciens))\)

Votre réponse :

Texte : inputlines897.txt

Zone de saisie de texte

Clavier	Action
`F1`	Afficher une aide technique
`F2`	Afficher une aide pédagogique
`Ctrl-A`	Tout sélectionner
`Ctrl-C`	Copier la sélection dans le presse-papier
`Ctrl-V`	Copier le presse-papier dans la sélection
`Ctrl-X`	Couper la sélection et la copier dans le presse-papier
`Ctrl-Z`	Annuler la modification
`Maj-Ctrl-Z`	Rétablir la modification

Menu	Action
	Ré-initialiser les sorties
	Faire apparaître le menu d'aide
	Valider la zone de saisie
	Initialiser la zone de saisie
	Charger le contenu d'un fichier dans la zone de saisie
	Sauvegarder le contenu de la zone de saisie dans un fichier
	Imprimer le contenu de la zone de saisie

Une solution possible :

Quel est le nom des musiciens du groupe AC/DC ?

de l'algèbre relationnelle au calcul relationnel

Exprimer en calcul relationnel de domaine et en calcul relationnel de n-uplets, l’expression algébrique suivante :

\(R=\Pi_{nom}(\sigma_{[groupe='AC/DC']}(musiciens))\)

sur la relation \(musiciens(nom,groupe)\)

On utilisera les mots not,and,or,in pour représenter les symboles des connecteurs logiques \(\neg,\land,\lor,\in\)

Votre réponse :

Texte : inputlines901.txt

Zone de saisie de texte

Clavier	Action
`F1`	Afficher une aide technique
`F2`	Afficher une aide pédagogique
`Ctrl-A`	Tout sélectionner
`Ctrl-C`	Copier la sélection dans le presse-papier
`Ctrl-V`	Copier le presse-papier dans la sélection
`Ctrl-X`	Couper la sélection et la copier dans le presse-papier
`Ctrl-Z`	Annuler la modification
`Maj-Ctrl-Z`	Rétablir la modification

Menu	Action
	Ré-initialiser les sorties
	Faire apparaître le menu d'aide
	Valider la zone de saisie
	Initialiser la zone de saisie
	Charger le contenu d'un fichier dans la zone de saisie
	Sauvegarder le contenu de la zone de saisie dans un fichier
	Imprimer le contenu de la zone de saisie

Une solution possible :

Calcul relationnel de domaine

\(R=\{ nom \; | \; musiciens(nom,groupe) \; \wedge \; groupe='AC/DC'\}\)

\(R=\{ n \; | \; musiciens(nom:n,groupe:g) \; \wedge \; g='AC/DC'\}\)

Calcul relationnel de n-uplets

\(R=\{ m.nom \; | \; musiciens(m) \; \wedge \; m.groupe='AC/DC'\}\)

de l'algèbre relationnelle à une requête SQL

A partir de l’expression algébrique suivante :

\(R=\Pi_{groupe}(\sigma_{[style='Rock']}(concerts))\)

écrire la requête SQL correspondante.

Votre réponse :

sql : concerts.sql

CREATE TABLE concerts (groupe varchar(20) , style varchar(20));
CREATE TABLE musiciens (nom varchar(20) , groupe varchar(20));
CREATE TABLE preferences (nom varchar(20) , style varchar(20));

INSERT INTO concerts(groupe,style) VALUES('AC/DC','Hard');
INSERT INTO concerts(groupe,style) VALUES('Led Zeppelin','Hard');
INSERT INTO concerts(groupe,style) VALUES('Rolling Stones','Rock');
INSERT INTO concerts(groupe,style) VALUES('Led Zeppelin','Rock');

INSERT INTO musiciens (nom,groupe) VALUES('Angus','AC/DC');
INSERT INTO musiciens (nom,groupe) VALUES('Malcom','AC/DC');
INSERT INTO musiciens (nom,groupe) VALUES('Keith','Rolling Stones');
INSERT INTO musiciens (nom,groupe) VALUES('Jimmy','Led Zeppelin');
INSERT INTO musiciens (nom,groupe) VALUES('Joe','Aerosmith');
INSERT INTO musiciens (nom,groupe) VALUES('Pete','The Who');

INSERT INTO preferences (nom,style) VALUES('Angus','Blues');
INSERT INTO preferences (nom,style) VALUES('Malcom','Hard');
INSERT INTO preferences (nom,style) VALUES('Keith','Blues');
INSERT INTO preferences (nom,style) VALUES('Keith','Rock');
INSERT INTO preferences (nom,style) VALUES('Charlie','Jazz');

/* a revoir : le model a change
SELECT * FROM Concert;
SELECT * FROM Jouer;
SELECT * FROM Musicien;

(SELECT style FROM musicien WHERE nom='Young')
EXCEPT
(SELECT style FROM concert NATURAL JOIN jouer NATURAL JOIN musicien WHERE  nom='Young');

SELECT style FROM musicien NATURAL JOIN jouer WHERE nom='Young'
AND style NOT IN (SELECT style FROM concert NATURAL JOIN jouer);

SELECT style
FROM musicien m
WHERE nom='Young' AND
NOT EXISTS(SELECT *
            FROM concert NATURAL JOIN jouer
            WHERE  m.style=style);
SELECT style
FROM musicien m
WHERE NOT EXISTS(SELECT *
                 FROM concert
                 WHERE m.style=style);
*/

Output

Interpréteur

Menu	Action
	Ré-initialiser les sorties
	Faire apparaître le menu d'aide
	Interpréter le programme

Editeur

Menu	Raccouci	Action
	`Ctrl+N`	Initialiser l'éditeur
	`Ctrl+O`	Charger le contenu d'un fichier dans l'éditeur
	`Ctrl+S`	Sauvegarder le contenu de l'éditeur dans un fichier
	`Ctrl+P`	Imprimer le contenu de l'éditeur
	`Ctrl+Z`	Annuler la dernière modification
	`Maj+Ctrl+Z`	Rétablir la modification précedente
	`Ctrl+F`	Chercher une expression dans l'éditeur
	`Maj+Ctrl+F`	Chercher et remplacer une expression par une autre
	`F10`	Ouvrir une documentation du langage

Raccourci	Action
`F1`	Afficher cette aide
`Tab`	Indenter la sélection
`Maj+Tab`	Désindenter la sélection
`Ctrl+A`	Sélectionner le contenu de l'éditeur
`Ctrl+C`	Copier la sélection dans le presse-papier
`Ctrl+V`	Remplacer la sélection par le contenu du presse-papier
`Ctrl+X`	Supprimer la sélection et la copier dans le presse-papier
`Maj+Ctrl+R`	Chercher et remplacer une expression par une autre dans tout l'éditeur

Une solution possible :

SELECT groupe FROM concerts WHERE style='Rock';

de l'algèbre relationnelle à un arbre de requête

A partir de l’expression algébrique suivante :

\(R=\Pi_{nom}(\sigma_{[groupe='AC/DC']}(musiciens))\)

construire l’arbre de requêtes correspondant

Votre réponse :

Arbre de requêtes : graph909.json


Tables Opérateurs unaires Opérateurs binaires

Vue d'ensemble
	CREATE TABLE concerts (groupe varchar(20) , style varchar(20)); CREATE TABLE musiciens (nom varchar(20) , groupe varchar(20)); CREATE TABLE preferences (nom varchar(20) , style varchar(20)); INSERT INTO concerts(groupe,style) VALUES('AC/DC','Hard'); INSERT INTO concerts(groupe,style) VALUES('Led Zeppelin','Hard'); INSERT INTO concerts(groupe,style) VALUES('Rolling Stones','Rock'); INSERT INTO concerts(groupe,style) VALUES('Led Zeppelin','Rock'); INSERT INTO musiciens (nom,groupe) VALUES('Angus','AC/DC'); INSERT INTO musiciens (nom,groupe) VALUES('Malcom','AC/DC'); INSERT INTO musiciens (nom,groupe) VALUES('Keith','Rolling Stones'); INSERT INTO musiciens (nom,groupe) VALUES('Jimmy','Led Zeppelin'); INSERT INTO musiciens (nom,groupe) VALUES('Joe','Aerosmith'); INSERT INTO musiciens (nom,groupe) VALUES('Pete','The Who'); INSERT INTO preferences (nom,style) VALUES('Angus','Blues'); INSERT INTO preferences (nom,style) VALUES('Malcom','Hard'); INSERT INTO preferences (nom,style) VALUES('Keith','Blues'); INSERT INTO preferences (nom,style) VALUES('Keith','Rock'); INSERT INTO preferences (nom,style) VALUES('Charlie','Jazz'); /* a revoir : le model a change SELECT * FROM Concert; SELECT * FROM Jouer; SELECT * FROM Musicien; (SELECT style FROM musicien WHERE nom='Young') EXCEPT (SELECT style FROM concert NATURAL JOIN jouer NATURAL JOIN musicien WHERE nom='Young'); SELECT style FROM musicien NATURAL JOIN jouer WHERE nom='Young' AND style NOT IN (SELECT style FROM concert NATURAL JOIN jouer); SELECT style FROM musicien m WHERE nom='Young' AND NOT EXISTS(SELECT * FROM concert NATURAL JOIN jouer WHERE m.style=style); SELECT style FROM musicien m WHERE NOT EXISTS(SELECT * FROM concert WHERE m.style=style); */ ----

Vue d'ensemble

CREATE TABLE concerts (groupe varchar(20) , style varchar(20));
CREATE TABLE musiciens (nom varchar(20) , groupe varchar(20));
CREATE TABLE preferences (nom varchar(20) , style varchar(20));

/* a revoir : le model a change
SELECT * FROM Concert;
SELECT * FROM Jouer;
SELECT * FROM Musicien;

(SELECT style FROM musicien WHERE nom='Young')
EXCEPT
(SELECT style FROM concert NATURAL JOIN jouer NATURAL JOIN musicien WHERE  nom='Young');

SELECT style FROM musicien NATURAL JOIN jouer WHERE nom='Young'
AND style NOT IN (SELECT style FROM concert NATURAL JOIN jouer);

SELECT style 
FROM musicien m
WHERE nom='Young' AND
NOT EXISTS(SELECT * 
            FROM concert NATURAL JOIN jouer
            WHERE  m.style=style);
SELECT style 
FROM musicien m
WHERE NOT EXISTS(SELECT * 
                 FROM concert
                 WHERE m.style=style);
*/

----

nom
Angus
Malcom

Une solution possible :

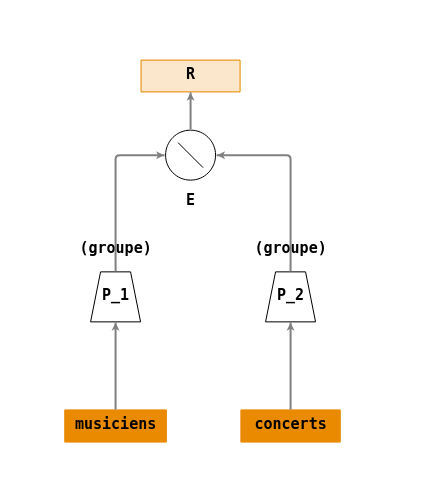
du langage naturel (en français) à un arbre de requêtes

construire l’arbre de requêtes pour rechercher :

« les groupes de musiciens qui ne font pas de concerts »

Votre réponse :

Arbre de requêtes : graph914.json


Tables Opérateurs unaires Opérateurs binaires

Vue d'ensemble
	CREATE TABLE concerts (groupe varchar(20) , style varchar(20)); CREATE TABLE musiciens (nom varchar(20) , groupe varchar(20)); CREATE TABLE preferences (nom varchar(20) , style varchar(20)); INSERT INTO concerts(groupe,style) VALUES('AC/DC','Hard'); INSERT INTO concerts(groupe,style) VALUES('Led Zeppelin','Hard'); INSERT INTO concerts(groupe,style) VALUES('Rolling Stones','Rock'); INSERT INTO concerts(groupe,style) VALUES('Led Zeppelin','Rock'); INSERT INTO musiciens (nom,groupe) VALUES('Angus','AC/DC'); INSERT INTO musiciens (nom,groupe) VALUES('Malcom','AC/DC'); INSERT INTO musiciens (nom,groupe) VALUES('Keith','Rolling Stones'); INSERT INTO musiciens (nom,groupe) VALUES('Jimmy','Led Zeppelin'); INSERT INTO musiciens (nom,groupe) VALUES('Joe','Aerosmith'); INSERT INTO musiciens (nom,groupe) VALUES('Pete','The Who'); INSERT INTO preferences (nom,style) VALUES('Angus','Blues'); INSERT INTO preferences (nom,style) VALUES('Malcom','Hard'); INSERT INTO preferences (nom,style) VALUES('Keith','Blues'); INSERT INTO preferences (nom,style) VALUES('Keith','Rock'); INSERT INTO preferences (nom,style) VALUES('Charlie','Jazz'); /* a revoir : le model a change SELECT * FROM Concert; SELECT * FROM Jouer; SELECT * FROM Musicien; (SELECT style FROM musicien WHERE nom='Young') EXCEPT (SELECT style FROM concert NATURAL JOIN jouer NATURAL JOIN musicien WHERE nom='Young'); SELECT style FROM musicien NATURAL JOIN jouer WHERE nom='Young' AND style NOT IN (SELECT style FROM concert NATURAL JOIN jouer); SELECT style FROM musicien m WHERE nom='Young' AND NOT EXISTS(SELECT * FROM concert NATURAL JOIN jouer WHERE m.style=style); SELECT style FROM musicien m WHERE NOT EXISTS(SELECT * FROM concert WHERE m.style=style); */ ----

Vue d'ensemble

CREATE TABLE concerts (groupe varchar(20) , style varchar(20));
CREATE TABLE musiciens (nom varchar(20) , groupe varchar(20));
CREATE TABLE preferences (nom varchar(20) , style varchar(20));

/* a revoir : le model a change
SELECT * FROM Concert;
SELECT * FROM Jouer;
SELECT * FROM Musicien;

(SELECT style FROM musicien WHERE nom='Young')
EXCEPT
(SELECT style FROM concert NATURAL JOIN jouer NATURAL JOIN musicien WHERE  nom='Young');

SELECT style FROM musicien NATURAL JOIN jouer WHERE nom='Young'
AND style NOT IN (SELECT style FROM concert NATURAL JOIN jouer);

SELECT style 
FROM musicien m
WHERE nom='Young' AND
NOT EXISTS(SELECT * 
            FROM concert NATURAL JOIN jouer
            WHERE  m.style=style);
SELECT style 
FROM musicien m
WHERE NOT EXISTS(SELECT * 
                 FROM concert
                 WHERE m.style=style);
*/

----

groupe
Aerosmith
The Who

Une solution possible :

Fichier de rejeu Close

Indication Close

A propos de... Close

Commentaire Close

Systèmes d'Information

Archives

Aide

En-tête

Pied de page

Généralités

Concerts

Votre réponse :

Une solution possible :

Votre réponse :

Zone de saisie de texte

Une solution possible :

Votre réponse :

Zone de saisie de texte

Une solution possible :

Votre réponse :

Zone de saisie de texte

Une solution possible :

Votre réponse :

Zone de saisie de texte

Une solution possible :

Votre réponse :

Interpréteur

Editeur

Une solution possible :

Votre réponse :

Tables

Opérateurs unaires

Opérateurs binaires

Une solution possible :

Votre réponse :

Tables

Opérateurs unaires

Opérateurs binaires

Une solution possible :