Fichier de rejeu Close
Indication Close
A propos de... Close
Commentaire Close
Systèmes d'Information
- Notions mathématiques
- Calcul relationnel
- Algèbre relationnelle
- Langage de requêtes
- Arbre de requêtes
- Exercices
- Introduction
- Commandes de bases
- Langage de définition de données (LDD)
- Langage de manipulation de données (LMD)
- Types de données
- Exercice
- Dépendances fonctionnelles
- Décomposition de relations
- Inférence logique
- Normalisation
- Aux pays des bières
- Modélisation
- Exercices

© Your Copyright
Aide
Exercices
Cette partie reprend les exercices abordés dans ce chapitre du cours pour illustrer les notions mathématiques sur lesquelles reposent les bases de données relationnelles. D’autres exercices sont également proposés à titre d’entraînement.
Vu en cours
Créer un ensemble de points défini par les coordonnées (x,y) et insérer (INSERT INTO ... VALUES ...) dans cet ensemble les points définissant un carré de 100 unités de côté, centré en (0,0) dans un repère (Oxy).
Votre réponse :
Une solution possible :
CREATE TABLE points(x FLOAT,y FLOAT);
INSERT INTO points(x,y) VALUES (-50,-50);
INSERT INTO points(x,y) VALUES (50,-50);
INSERT INTO points(x,y) VALUES (50,50);
INSERT INTO points(x,y) VALUES (-50,50);
SELECT * from points;
Lors de l’exécution de ces requêtes SQL, on remarquera la représentation tabulaire du résultat sous forme de lignes et de colonne qui ne sera pas sans rappeler les tableurs type Excel. Les noms de colonnes (x,y) représentent les attributs (propriétés) de la table (entité). Les lignes représentent les informations (éléments,enregistrements,n-uplets) que l’on, insère dans la table.
Votre réponse :
Représenter l’ensemble des chiffres pairs en intension et écrire la requête SQL correspondante.
Zone de saisie de texte
| Clavier | Action |
|---|---|
| F1 | Afficher une aide technique |
| F2 | Afficher une aide pédagogique |
| Ctrl-A | Tout sélectionner |
| Ctrl-C | Copier la sélection dans le presse-papier |
| Ctrl-V | Copier le presse-papier dans la sélection |
| Ctrl-X | Couper la sélection et la copier dans le presse-papier |
| Ctrl-Z | Annuler la modification |
| Maj-Ctrl-Z | Rétablir la modification |
| Menu | Action |
|---|---|
| Ré-initialiser les sorties | |
| Faire apparaître le menu d'aide | |
| Valider la zone de saisie | |
| Initialiser la zone de saisie | |
| Charger le contenu d'un fichier dans la zone de saisie | |
| Sauvegarder le contenu de la zone de saisie dans un fichier | |
| Imprimer le contenu de la zone de saisie |
Une solution possible :
Ensemble des chiffres pairs en intension :
- \(E = \{ x \; \mid \; x \in \mathbb{N} \land x \equiv 0 \mod 2 \land (x>=0 \land x<10) \}\)
Requête SQL pour récupérer les chiffres pairs dans l’ensemble des entiers :
SELECT x FROM E WHERE x%2 = 0 AND x >=0 AND x < 10;
Votre réponse :
En utilisant les opérations ensemblistes d’union et d’intersection (\(\cup,\cap\)), vérifier à l’aide de requêtes SQL, l’expression suivante :
- \(card(E_1 \cup E_2) = card(E_1) + card(E_2) - card(E_1 \cap E_2)\)
lorsque \(E_1\) représente l’ensemble des chiffres pairs et \(E_2\) l’ensemble des chiffres impairs (\(E_2\))
Une solution possible :
- \(card(E_1 \cup E_2) = card(E_1) + card(E_2) - card(E_1 \cap E_2)\)
SELECT count(*) AS "card(E1 Union E2)"
FROM (SELECT * FROM E1 UNION SELECT * FROM E2);
SELECT "" AS "=";
SELECT count(*) AS "card(E1)" FROM E1;
SELECT "" AS "+";
SELECT count(*) AS "card(E2)" FROM E2;
SELECT "" AS "-";
SELECT count(*) AS "card(E1 Intersect E2)"
FROM (SELECT * FROM E1 INTERSECT SELECT * FROM E2);
Votre réponse :
En utilisant les opérations ensemblistes d’intersection et de différence (\(\cap,\setminus\)), vérifier à l’aide de requêtes SQL, l’expression suivante :
- \(card(E_1 \setminus E_2) = card(E_1) - card(E_1 \cap E_2)\)
lorsque \(E_1\) représente l’ensemble des chiffres arabes (\(E\)) et \(E_2\) l’ensemble des chiffres impairs (\(Digit\_odd\))
Une solution possible :
\(card(E_1 \setminus E_2) = card(E_1) - card(E_1 \cap E_2)\)
SELECT count(*) AS "card(E1 Minus E2)"
FROM (SELECT * FROM E1 EXCEPT SELECT * FROM E2);
SELECT "" AS "=";
SELECT count(*) AS "card(E1)" FROM E1;
SELECT "" AS "-";
SELECT count(*) AS "card(E1 Intersect E2)"
FROM (SELECT * FROM E1 INTERSECT SELECT * FROM E2);
Requête : « Créer une requête SQL permettant de vérifier que la différence entre l’ensemble des chiffres (E) et l’union des chiffres pairs (E1) et impairs (E2) est nulle «
Votre réponse :
Une solution possible :
SELECT x AS "digits" FROM E;
-- create view E1 : chiffres pairs --
CREATE VIEW E1 AS
SELECT * FROM E WHERE x%2=0;
SELECT x AS "event digits" FROM E1;
-- create view E2 : chiffres impairs --
CREATE VIEW E2 AS
SELECT * FROM E
EXCEPT
SELECT * FROM E1;
SELECT x AS "odd digits" FROM E2;
-- card(E \ (E U E2)) = 0 --
SELECT count(*) AS "card(E \ (E U E2)) = 0"
FROM E
WHERE NOT EXISTS (
SELECT * FROM E1
UNION
SELECT * FROM E2
);
Votre réponse :
En utilisant les opérations ensemblistes d’union, d’intersection et de différence (\(\cup, \cap,\setminus\)), vérifier à l’aide de requêtes SQL, l’expression suivante :
- \((A \cup B) \setminus (A \cap B)= \emptyset\)
lorsque \(A\) représente l’ensemble des chiffres arabes dans l’ordre croissant et \(B\) l’ensemble des chiffres arabes dans l’ordre décroissant.
On créera une vue pour représenter l’ensemble \(B\) en utilisant l’ensemble \(A\) dans une requête pour définir les chiffres arabes dans l’ordre décroissant.
sql : essai.sqlOutput
Une solution possible :
- \((A \cup B) \setminus (A \cap B)= \emptyset\)
CREATE VIEW B AS
SELECT * FROM A ORDER BY x DESC;
SELECT * FROM A;
SELECT * FROM B;
SELECT COUNT(*)
FROM
(
SELECT x FROM A UNION SELECT x FROM B
EXCEPT
SELECT x FROM A INTERSECT SELECT x FROM B
)
A partir de l’ensemble des entiers définis dans l’intervalle \(E=[-2,11]\), créer dans une vue (E_1) le sous-ensemble des chiffres pairs.
A partir de ces deux ensembles, récupérer dans une vue (E_2) le sous-ensemble des chiffres qui ne sont pas dans
le sous-ensemble des chiffres pairs (récupérer donc l’ensemble des chiffres impairs :) ).
Votre réponse :
Une solution possible :
SELECT * FROM E;
-- create view E1 (even digits) --
CREATE VIEW E1 AS
SELECT x FROM E WHERE x%2=0 AND x>=0 AND x<10;
SELECT x AS "even digits" FROM E1;
-- create view E2 (odd digits) --
CREATE VIEW E2 AS
SELECT x FROM E WHERE x>0 AND x<10 AND x NOT IN (SELECT x FROM E1);
SELECT x AS "odd digits" FROM E2;
-- card(E1\E) = 0 => E1 inclus dans E --
SELECT count(*) AS "card(E1\E)" FROM E1 EXCEPT SELECT x FROM E;
-- card(E\E1) --
SELECT count(*) AS "card(E\E1)" FROM E EXCEPT SELECT x FROM E1;
-- card(E2\E) = 0 => E2 inclus dans E ---
SELECT count(*) AS "card(E2\E)" FROM E2 EXCEPT SELECT x FROM E;
-- card(E\E2) --
SELECT count(*) AS "card(E\E2)" FROM E EXCEPT SELECT x FROM E2;
- A partir de l’ensemble des entiers (
E) de la base de données - créer dans des vues (
E1,E2) les sous-ensembles des chiffres pairs, impairs. - créer une vue (
E_numbers) sur l’ensemble des nombres qui ne sont pas des chiffres . - créer une vue (
E_Union) contituant l’union de ces trois parties.
- créer dans des vues (
Vérifier que l’ensemble des parties (E_Union) est bien égal à l’ensemble (E-E_Union=0).
Votre réponse :
Une solution possible :
SELECT * FROM E;
-- create view E1 : chiffres pairs --
CREATE VIEW E1 AS
SELECT x FROM E WHERE x%2=0 AND x>=0 AND x<10;
-- create view E2 : chiffres impairs --
CREATE VIEW E2 AS
SELECT x FROM E WHERE x>0 AND x<10 AND x NOT IN (SELECT x FROM E1);
SELECT x AS "even digits" FROM E1;
SELECT x AS "odd digits" FROM E2;
-- create view E_numbers --
CREATE VIEW E_numbers AS
SELECT x FROM E WHERE x NOT IN (SELECT x FROM E1) AND x NOT IN (SELECT x FROM E2);
SELECT x AS "numbers" FROM E_numbers;
-- create view E_union = E_numbers + E1 + E2 --
CREATE VIEW E_union AS
SELECT x FROM E_numbers
UNION
SELECT x FROM E1 UNION SELECT x FROM E2;
-- E - E_union = 0 --
SELECT count(*) AS "E-E_union=0" FROM (SELECT x FROM E EXCEPT SELECT x FROM E_union);
Cet exercice est extrait du site de Bertrand Liaudet dans son cours sur la « théorie des ensembles et bases de données ».
Enoncé : 200 élèves participent à une journée de sport. 3 sports sont au programme : le foot, la natation et la course à pieds. Chaque élève peut participer à 1, 2 ou 3 sports. Avec les informations ci-dessous, trouver le nombre d’élèves qui participent à un seul sport, à 2 sports et à trois sports :
- 10 élèves sont blessés et ne participent pas
- 18 participent au 3 sports
- 103 ne font que 2 sports
- 79 font du foot et de la natation
- 19 ne font que le la course
- 129 font de la natation dont 40 que de ça .
Indice :
Cet exercice pourra être résolu par une méthode de représentation d’ensembles sous forme de diagramme de Venn et de calcul de cardinalité d’ensembles.
Votre réponse :
Zone de saisie de texte
| Clavier | Action |
|---|---|
| F1 | Afficher une aide technique |
| F2 | Afficher une aide pédagogique |
| Ctrl-A | Tout sélectionner |
| Ctrl-C | Copier la sélection dans le presse-papier |
| Ctrl-V | Copier le presse-papier dans la sélection |
| Ctrl-X | Couper la sélection et la copier dans le presse-papier |
| Ctrl-Z | Annuler la modification |
| Maj-Ctrl-Z | Rétablir la modification |
| Menu | Action |
|---|---|
| Ré-initialiser les sorties | |
| Faire apparaître le menu d'aide | |
| Valider la zone de saisie | |
| Initialiser la zone de saisie | |
| Charger le contenu d'un fichier dans la zone de saisie | |
| Sauvegarder le contenu de la zone de saisie dans un fichier | |
| Imprimer le contenu de la zone de saisie |
Une solution possible :
Cet exercice pourra être résolu par une méthode de représentation d’ensembles sous forme de diagramme de Venn et de calcul de cardinalité d’ensembles.
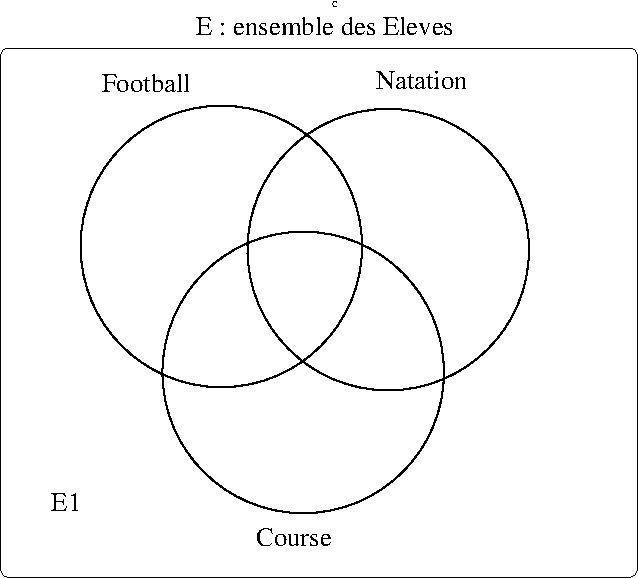
Ces ensembles représentent l’ensemble des élèves (\(E_1\)) qui ne feront pas de sports et les ensembles d’élèves qui font un ou plusieurs sports :
- \(E= E_1 \cup Football \cup Natation \cup Course\)
- où :
- \(card(E)=card(E_1)+card(Football)+card(Natation)+card(Course)=200\)
On défini alors un partitionnement de l’ensemble des élèves (\(E\)) en sous-ensembles :
- les élèves qui ne pourront participer à la journée de sport (\(E_1)\)
- les élèves qui participeront à un seul sport (\(E_2,E_3,E_4)\)
- les élèves qui participeront à deux sports (\(E_5,E_6,E_7)\)
- les élèves qui participeront aux trois sports(\(E_8)\)
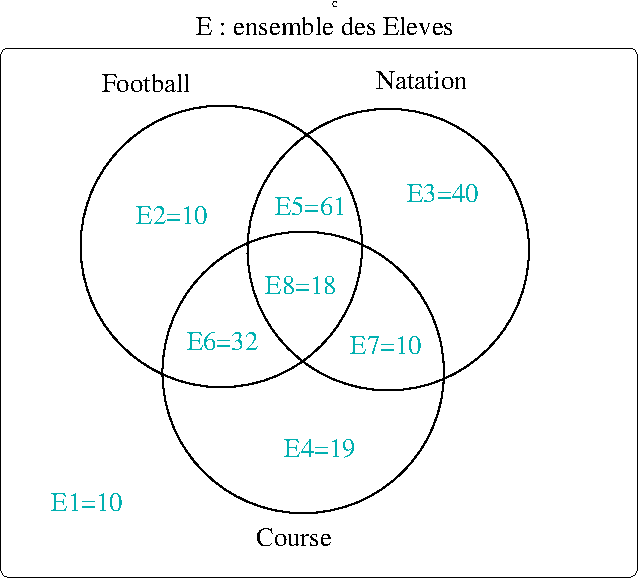
représentés par le diagramme de Venn ci-dessous :
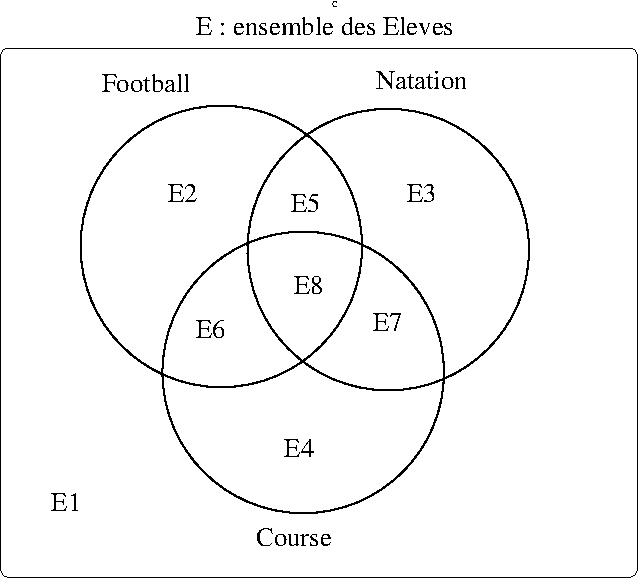
A partir des données du problème on peut déjà identifier :
10 élèves sont blessés et ne participent pas
\(\Rightarrow card(E_1)=10\)
18 participent au 3 sports
\(\Rightarrow card(E_8)=18\)
103 ne font que 2 sports
79 font du foot et de la natation
19 ne font que le la course
\(\Rightarrow card(E_4)=19\)
129 font de la natation dont 40 que de ça .
\(\Rightarrow card(E_3)=40\)
représentés par le diagramme de Venn ci-dessous :
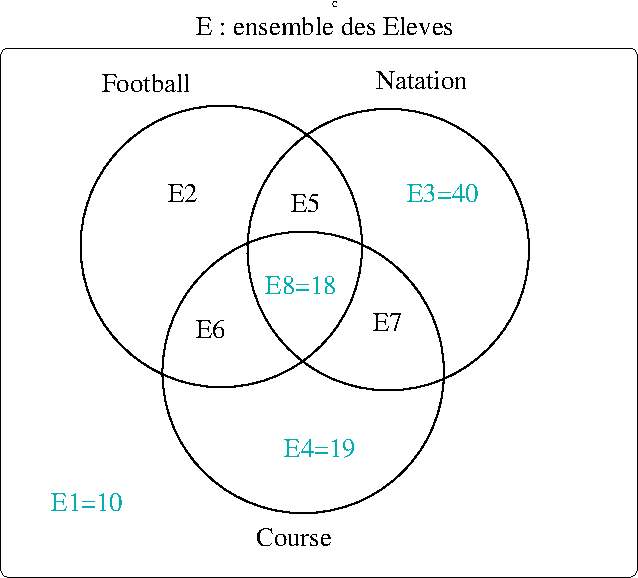
79 font du foot et de la natation :
- \(card(E_5)+card(E_8)=79\)
- \(card(E_5)+18=79\)
\(\Rightarrow card(E_5)=61\)
129 font de la natation dont 40 que de ça :
- \(card(E_3)+card(E_5)+card(E_7)+card(E_8)=129\)
- \(40+61+card(E_7)+18=129\)
\(\Rightarrow card(E_7)=10\)
103 ne font que 2 sports
- \(card(E_5)+card(E_6)+card(E_7)=103\)
- \(61+card(E_6)+10=103\)
\(\Rightarrow card(E_6)=32\)
200 élèves en tout :
- \(card(E_1)+card(E_2)+card(E_3)+card(E_4)+card(E_5)+card(E_6)+card(E_7)+card(E_8)=200\)
- \(10+card(E_2)+40+19+61+32+10+18=200\)
\(\Rightarrow card(E_2)=10\)
On obtient donc la partition suivante de l’ensemble des élèves pour la journée de sport :
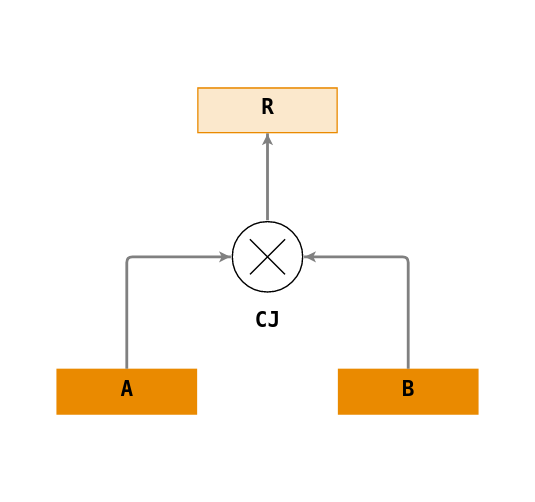
Créer l’arbre de requêtes qui permettra de vérifier que les deux ensembles A et B , représentés ci-dessous, sont égaux.
Votre réponse :
Arbre de requêtes : AB.json
TablesOpérateurs unairesOpérateurs binaires |
| Vue d'ensemble | |
|---|---|
|
|
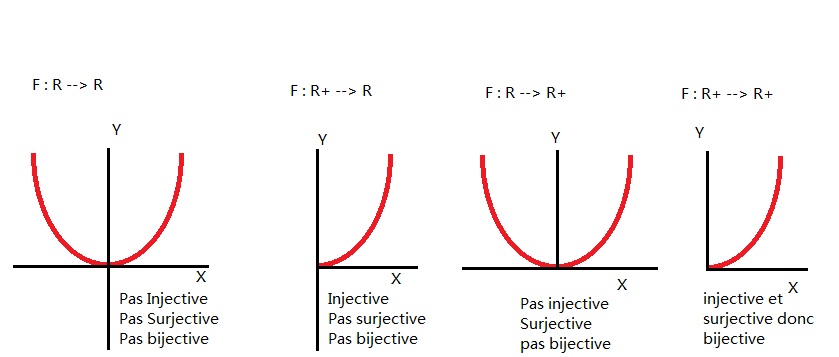
Suivant les ensembles de départ et d’arrivée :
- \(f : \mathbb{R} \rightarrow \mathbb{R}\)
- \(f : \mathbb{R_+} \rightarrow \mathbb{R}\)
- \(f : \mathbb{R} \rightarrow \mathbb{R_+}\)
- \(f : \mathbb{R_+} \rightarrow \mathbb{R_+}\)
La fonction \(f : x \longrightarrow x^2\) est-elle :
- injective
- surjective
- bijective
- aucun des trois cas possibles
Votre réponse :
Zone de saisie de texte
| Clavier | Action |
|---|---|
| F1 | Afficher une aide technique |
| F2 | Afficher une aide pédagogique |
| Ctrl-A | Tout sélectionner |
| Ctrl-C | Copier la sélection dans le presse-papier |
| Ctrl-V | Copier le presse-papier dans la sélection |
| Ctrl-X | Couper la sélection et la copier dans le presse-papier |
| Ctrl-Z | Annuler la modification |
| Maj-Ctrl-Z | Rétablir la modification |
| Menu | Action |
|---|---|
| Ré-initialiser les sorties | |
| Faire apparaître le menu d'aide | |
| Valider la zone de saisie | |
| Initialiser la zone de saisie | |
| Charger le contenu d'un fichier dans la zone de saisie | |
| Sauvegarder le contenu de la zone de saisie dans un fichier | |
| Imprimer le contenu de la zone de saisie |
Une solution possible :
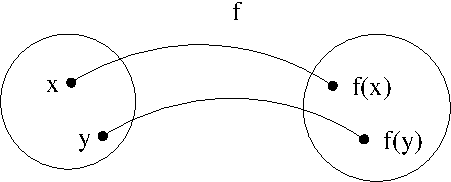
dans le premier cas (\(f : \mathbb{R} \rightarrow \mathbb{R}\)) la fonction (\(f : x \longrightarrow x^2\)) est :
- non-injective : deux éléments de l’ensemble de départ ont la même image \(\{ -1,+1 \} \rightarrow \{ +1 \}\)
- non-surjective : des éléments de l’ensemble d’arrivée n’ont pas d’antécédent (ex : \(y=-4\) n’a pas d’antécédent)
- non-bijective : puisque non-injective et non-surjective
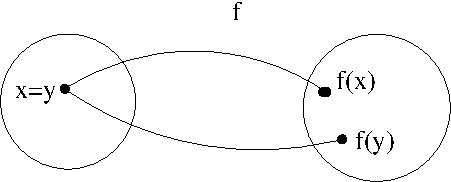
dans le deuxième cas (\(f : \mathbb{R_+} \rightarrow \mathbb{R}\)) la fonction (\(f : x \longrightarrow x^2\)) est :
- injective : Les éléments de l’ensemble d’arrivée ont au plus un antécédent
- non-surjective : des éléments de l’ensemble d’arrivée n’ont pas d’antécédent (ex : \(y=-4\) n’a pas d’antécédent)
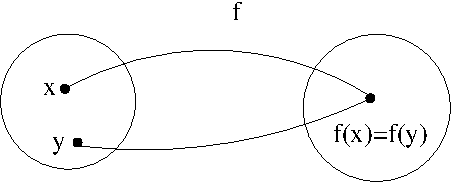
dans le troisième cas (\(f : \mathbb{R} \rightarrow \mathbb{R_+}\)) la fonction (\(f : x \longrightarrow x^2\)) est :
- non-injective : deux éléments de l’ensemble de départ ont la même image \(\{ -1,+1 \} \rightarrow \{ +1 \}\)
- surjective : tout élément de l’ensemble d’arrivée a au moins un antécédent
- non-bijective : puisque non-injective
dans le dernier cas (\(f : \mathbb{R_+} \rightarrow \mathbb{R_+}\)) la fonction (\(f : x \longrightarrow x^2\)) est :
- injective : Les éléments de l’ensemble d’arrivée ont au plus un antécédent
- surjective : tout élément de l’ensemble d’arrivée a au moins un antécédent
- bijective : puisque injective et surjective
Ecriture d’une requête SQL pour obtenir une différence symétrique entre deux ensembles \(A,B\) :
Votre réponse :
Une solution possible :
SELECT * FROM A;
SELECT * FROM B;
-- A xor B --
SELECT x AS "A xor B" FROM A WHERE x NOT IN (SELECT y FROM B)
UNION
SELECT y FROM B WHERE y NOT IN (SELECT x FROM A);
Pour aller plus loin : on peut aussi exprimer la disjonction exclusive avec l’opérateur de jointure FULL OUTER JOIN mais cet opérateur n’est pas implémenté en SQLite par contre le lecteur intéressé pourra le tester sous PostgreSQL par exemple.
Les différentes jointures (INNER,OUTER,NATURAL) seront détaillées dans le chapitre SQL.
code SQL pour la disjonction exclusive à l’aide de jointure :
SELECT COALESCE(A.x, B.y) AS "A xor B"
FROM A FULL OUTER JOIN B
ON A.x = B.y
WHERE A.x IS NULL OR B.y IS NULL;
Traduisez en proposition et implication la phrase suivante :
- « Pour que les étudiants réussissent, il faut qu’ils étudient. »
Faites la table de vérité correspondant et interpréter tous les cas.
Votre réponse :
Zone de saisie de texte
| Clavier | Action |
|---|---|
| F1 | Afficher une aide technique |
| F2 | Afficher une aide pédagogique |
| Ctrl-A | Tout sélectionner |
| Ctrl-C | Copier la sélection dans le presse-papier |
| Ctrl-V | Copier le presse-papier dans la sélection |
| Ctrl-X | Couper la sélection et la copier dans le presse-papier |
| Ctrl-Z | Annuler la modification |
| Maj-Ctrl-Z | Rétablir la modification |
| Menu | Action |
|---|---|
| Ré-initialiser les sorties | |
| Faire apparaître le menu d'aide | |
| Valider la zone de saisie | |
| Initialiser la zone de saisie | |
| Charger le contenu d'un fichier dans la zone de saisie | |
| Sauvegarder le contenu de la zone de saisie dans un fichier | |
| Imprimer le contenu de la zone de saisie |
Une solution possible :
On peut reformuler la phrase : « Pour que les étudiants réussissent, il faut qu’ils étudient. »
par : « Si les étudiants étudient alors ils réussissent »
D’où les propositions :
- \(P\) : « les étudiants étudient »
- \(Q\) : « les étudiants réussissent »
En représentant la table de vérité de l’implication (Si P alors Q) :
Implication P Q P => Q 0 0 1 0 1 1 1 0 0 1 1 1
On peut interpréter les différents cas :
- \(P,Q\) sont toutes deux fausses : les étudiants n’étudient pas et ils ne réussissent pas (c’est classique !)
- \(P\) fausse, \(Q\) vraie : les étudiants n’étudient pas et ils réussissent (ça arrive, mais c’est rare !)
- \(P\) vraie, \(Q\) fausse : les étudiants étudient et ils ne réussissent pas (ce n’est pas possible !)
- \(P\) vraie, \(Q\) vraie : les étudiants étudient et ils réussissent (c’est normal !)
Complémentaires
Soit l’ensemble \(E\) défini en extension :
- \(E=\{1,2,4,8,16,32,64,128,256 \}\)
Proposez une définition en intension (compréhension) de cet ensemble.
Exprimer en français ce que représente cet ensemble.
Votre réponse :
Zone de saisie de texte
| Clavier | Action |
|---|---|
| F1 | Afficher une aide technique |
| F2 | Afficher une aide pédagogique |
| Ctrl-A | Tout sélectionner |
| Ctrl-C | Copier la sélection dans le presse-papier |
| Ctrl-V | Copier le presse-papier dans la sélection |
| Ctrl-X | Couper la sélection et la copier dans le presse-papier |
| Ctrl-Z | Annuler la modification |
| Maj-Ctrl-Z | Rétablir la modification |
| Menu | Action |
|---|---|
| Ré-initialiser les sorties | |
| Faire apparaître le menu d'aide | |
| Valider la zone de saisie | |
| Initialiser la zone de saisie | |
| Charger le contenu d'un fichier dans la zone de saisie | |
| Sauvegarder le contenu de la zone de saisie dans un fichier | |
| Imprimer le contenu de la zone de saisie |
Une solution possible :
Définition en intension :
\(E=\{ 2^n | n \in \mathbb{N} \land n>=0 \land n<=8 \}\)
Cet ensemble représente les puissances de 2 allant de 1 jusqu’à 256.
Si l’on veut étendre cet ensemble à tous les entiers naturels :
- \(E=\{ 2^n | n \in \mathbb{N} \}\)
Soit l’ensemble \(E\) :
- \(E=\{1,2,3\}\)
Trouver l’ensemble de toutes les parties \(\mathscr{P}(E)\) de l’ensemble \(E\).
Vérifier que \(card(\mathscr{P}(E))=2^{card(E)}\)
Votre réponse :
Zone de saisie de texte
| Clavier | Action |
|---|---|
| F1 | Afficher une aide technique |
| F2 | Afficher une aide pédagogique |
| Ctrl-A | Tout sélectionner |
| Ctrl-C | Copier la sélection dans le presse-papier |
| Ctrl-V | Copier le presse-papier dans la sélection |
| Ctrl-X | Couper la sélection et la copier dans le presse-papier |
| Ctrl-Z | Annuler la modification |
| Maj-Ctrl-Z | Rétablir la modification |
| Menu | Action |
|---|---|
| Ré-initialiser les sorties | |
| Faire apparaître le menu d'aide | |
| Valider la zone de saisie | |
| Initialiser la zone de saisie | |
| Charger le contenu d'un fichier dans la zone de saisie | |
| Sauvegarder le contenu de la zone de saisie dans un fichier | |
| Imprimer le contenu de la zone de saisie |
Une solution possible :
\(\mathscr{P}(E)=\{ \{ \}, \{ 1 \}, \{ 2 \}, \{ 3 \}, \{ 1,2 \},\{ 1,3 \},\{ 2,3 \},\{ 1,2,3 \} \}\)
on vérifie bien :
- \(card(\mathscr{P}(E))=2^{card(E)}\)
- \(8=2^3\)
Soit le code python suivant :
for i in [2,3,4] : for j in [1,2,3] : print (i**j)Représentez en extension l’ensemble des résultats affichés par ce code.
Remarque : en python
i**jsignifieià la puissancej( \(i^j\))
Votre réponse :
Zone de saisie de texte
| Clavier | Action |
|---|---|
| F1 | Afficher une aide technique |
| F2 | Afficher une aide pédagogique |
| Ctrl-A | Tout sélectionner |
| Ctrl-C | Copier la sélection dans le presse-papier |
| Ctrl-V | Copier le presse-papier dans la sélection |
| Ctrl-X | Couper la sélection et la copier dans le presse-papier |
| Ctrl-Z | Annuler la modification |
| Maj-Ctrl-Z | Rétablir la modification |
| Menu | Action |
|---|---|
| Ré-initialiser les sorties | |
| Faire apparaître le menu d'aide | |
| Valider la zone de saisie | |
| Initialiser la zone de saisie | |
| Charger le contenu d'un fichier dans la zone de saisie | |
| Sauvegarder le contenu de la zone de saisie dans un fichier | |
| Imprimer le contenu de la zone de saisie |
Une solution possible :
\(E=\{2,4,8,3,9,27,4,16,64 \}\)À partir des ensembles :
- \(abscisses=\{0,1\}\)
- \(ordonnees=\{0,1\}\)
- Définir en intension l’ensemble des coordonnées \((abscisses,ordonnees)\) d’un carré de côté unitaire.
- Créer en SQL les tables correspondantes aux
abscissesetordonnees. - Créer une vue dont le résultat représenterait les coordonnées de ce carré.
- Que pourrait-on faire pour créer dans une vue les coordonnées d’un cube unitaire.
Votre réponse :
Une solution possible :
- \(coordonnes=\{(x,y) | x\in abscisses \land y \in ordonnees \}\)
CREATE TABLE abscisses (x INTEGER);
CREATE TABLE ordonnees (y INTEGER);
INSERT INTO abscisses VALUES(0);
INSERT INTO abscisses VALUES(1);
INSERT INTO ordonnees VALUES(0);
INSERT INTO ordonnees VALUES(1);
CREATE VIEW coordonnees AS
SELECT * FROM abscisses,ordonnees;
SELECT * FROM coordonnees;
Pour créer dans une vue les coordonnées d’un cube unitaire, il faudrait créer un nouvel ensemble (table « altitudes ») avec les valeurs \(\{0,1\}\) et faire le produit cartésien entre les trois tables.
On considère l’ensemble des services représentant les informations sur les bars et les bieres qu’ils servent :
services(bar,biere)
Représentez en calcul relationnel de domaine la recherche des bars qui servent de la « Chouffe ».
Représentez en calcul relationnel de n-uplet la recherche des bières qui sont servies au « Bar du Coin ».
Votre réponse :
Zone de saisie de texte
| Clavier | Action |
|---|---|
| F1 | Afficher une aide technique |
| F2 | Afficher une aide pédagogique |
| Ctrl-A | Tout sélectionner |
| Ctrl-C | Copier la sélection dans le presse-papier |
| Ctrl-V | Copier le presse-papier dans la sélection |
| Ctrl-X | Couper la sélection et la copier dans le presse-papier |
| Ctrl-Z | Annuler la modification |
| Maj-Ctrl-Z | Rétablir la modification |
| Menu | Action |
|---|---|
| Ré-initialiser les sorties | |
| Faire apparaître le menu d'aide | |
| Valider la zone de saisie | |
| Initialiser la zone de saisie | |
| Charger le contenu d'un fichier dans la zone de saisie | |
| Sauvegarder le contenu de la zone de saisie dans un fichier | |
| Imprimer le contenu de la zone de saisie |
Une solution possible :
Les bars qui servent de la « Chouffe » (DRC)
- \(Q=\{bar | services(bar,biere='Chouffe')\}\)
Les bières servies au « Bar du Coin » (TRC)
- \(Q=\{s.biere | services(s) \land s.bar='Bar \; du \; Coin'\}\)
Les deux notations sont équivalentes, cependant la notation en calcul relationnel de n-uplet (TRC) est plus représentative sur la manipulation d’éléments dans un ensemble et de formulation logique.
On pourrait écrire de la même manière :
- \(Q=\{s.biere | s \in services \land s.bar='Bar \; du \; Coin'\}\)
qui définit bien la proposition logique que l’ensemble des éléments doit vérifier :
- \(Q=\{x | P(x) \}\)
où, dans notre cas la fonction caractéristique de l’ensemble est :
- \(P(x)= (x \in services \land x.bar='Bar \; du \; Coin')\)
on doit vérifier que le service proposant la biere en question est (appartient) bien dans l’ensemble des services et qu’il concernera le 'Bar du Coin'.
On considère l’ensemble des services représentant les informations sur les bars et les bieres qu’ils servent :
services(bar,biere)
Représentez en algèbre relationnelle la recherche des bars qui servent de la « Chouffe ».
Votre réponse :
Zone de saisie de texte
| Clavier | Action |
|---|---|
| F1 | Afficher une aide technique |
| F2 | Afficher une aide pédagogique |
| Ctrl-A | Tout sélectionner |
| Ctrl-C | Copier la sélection dans le presse-papier |
| Ctrl-V | Copier le presse-papier dans la sélection |
| Ctrl-X | Couper la sélection et la copier dans le presse-papier |
| Ctrl-Z | Annuler la modification |
| Maj-Ctrl-Z | Rétablir la modification |
| Menu | Action |
|---|---|
| Ré-initialiser les sorties | |
| Faire apparaître le menu d'aide | |
| Valider la zone de saisie | |
| Initialiser la zone de saisie | |
| Charger le contenu d'un fichier dans la zone de saisie | |
| Sauvegarder le contenu de la zone de saisie dans un fichier | |
| Imprimer le contenu de la zone de saisie |
Une solution possible :
les bars qui servent de la « Chouffe » (DRC)
- \(Q=\Pi_{(bar)}(\sigma_{[biere='Chouffe']}(services))\)
Lorsque l’expression utilise plusieurs opérateurs de l’algèbre relationnelle on peut décomposer la recherche en plusieurs étapes :
- \(R_1=\sigma_{[biere='Chouffe']}(services)\)
- \(R_2=\Pi_{(bar)}(R_1)\)
- \(Q=R_2\)
Attention : il ne faut pas inverser les opérations de restriction et projection. La requête ci-dessous ne sera pas valide :
- \(Q=\sigma_{[biere='Chouffe']}(\Pi_{(bar)}(services))\)
Le résultat de l’opération de projection (\(\Pi\)) ne permettra pas d’avoir accès à l’attribut biere pour pouvoir établir la condition (\([biere='Chouffe']\)) de l” opération de restriction (\(\sigma\)) .
Soit les deux relations suivantes :
- \(R(a,b,c),S(d,e)\)
Convertir l’expression \(\Pi_{(a,e)}(\sigma_{[b=d \land c=d]}(\times(R,S))\) en calcul relationnel de n-uplet.
Votre réponse :
Zone de saisie de texte
| Clavier | Action |
|---|---|
| F1 | Afficher une aide technique |
| F2 | Afficher une aide pédagogique |
| Ctrl-A | Tout sélectionner |
| Ctrl-C | Copier la sélection dans le presse-papier |
| Ctrl-V | Copier le presse-papier dans la sélection |
| Ctrl-X | Couper la sélection et la copier dans le presse-papier |
| Ctrl-Z | Annuler la modification |
| Maj-Ctrl-Z | Rétablir la modification |
| Menu | Action |
|---|---|
| Ré-initialiser les sorties | |
| Faire apparaître le menu d'aide | |
| Valider la zone de saisie | |
| Initialiser la zone de saisie | |
| Charger le contenu d'un fichier dans la zone de saisie | |
| Sauvegarder le contenu de la zone de saisie dans un fichier | |
| Imprimer le contenu de la zone de saisie |
Une solution possible :
\(R=\{(r.a,s.e) | R(r) \land S(s) \land r.b=s.d \land r.c=s.d\}\)
On aurait également pu décomposer le calcul relationnel :
- \(R_1=\{(r,s) | R(r) \land S(s) \}\) (produit cartésien)
- \(R_2=\{r_1 | R_1(r_1) \land r_1.b=r_1.d \land r_1.c=r_1.d \}\) (restriction)
- \(R=\{(r_2.a,r_2.e) | R_2(r_2) \}\) (projection)
qui représentera l’ordre d’application des opérateurs de l’algèbre relationnelle.
Remarque :
- on ne pourrait pas appliquer d’abord les restrictions puisque chacune des conditions s’applique sur les attributs des deux tables. Cette requête ne pourra donc pas être optimisée en appliquant les restrictions avant le produit cartésien.
On considère l’ensemble des services représentant les informations sur les bars et les bieres qu’ils servent :
services(bar,biere)
Représentez en arbre de requête la recherche des bars qui servent de la « Chouffe ».
Votre réponse :
Arbre de requêtes : graph1115.json
TablesOpérateurs unairesOpérateurs binaires |
| Vue d'ensemble | |
|---|---|
|
|
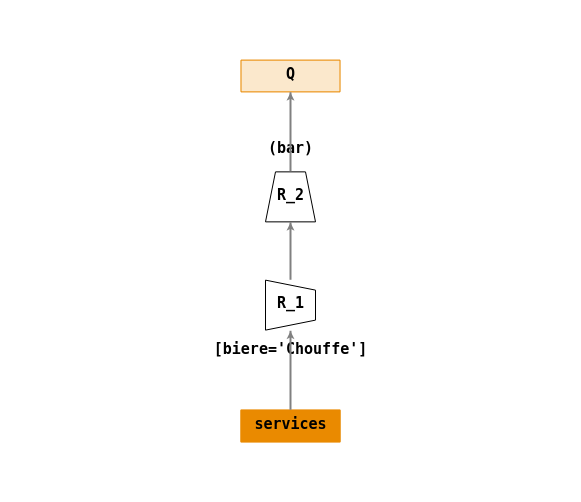
Une solution possible :
- \(R_1=\sigma_{[biere='Chouffe']}(services)\)
- \(R_2=\Pi_{(bar)}(R_1)\)
- \(Q=R_2\)
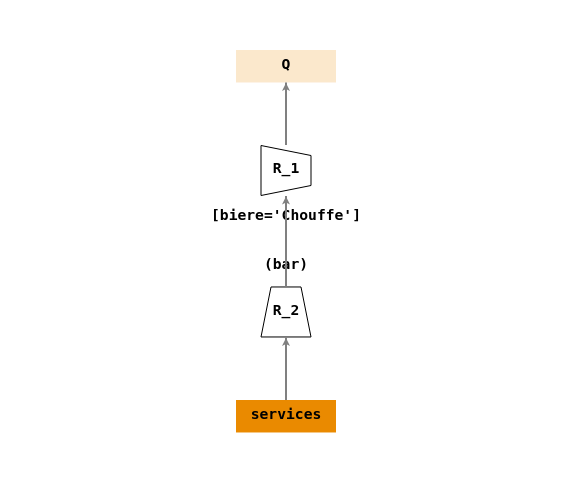
Attention : il ne faut pas inverser les opérations de restriction et projection
L’arbre de requêtes ci-dessous traitera d’abord l’opération de projection et nous n’aurons plus accès aux informations sur l’attributbierepour pouvoir faire l’opération de restriction.
On considère la table suivante :
- sportifs (nom,age,activite,categorie)
On souhaite rechercher les sportifs qui font du rugby ou qui sont « junior » mais pas les deux en même temps.
Ecrire la requête SQL qui permettra de retrouver ces sportifs.
Votre réponse :
Une solution possible :
Pour écrire cette requête on doit exclure les sportifs qui feraient du rugby et qui seraient en catégorie « junior »
On a donc une disjonction exclusive (\(\oplus\)) :
- \(P \oplus Q = (P \land \neg Q) \lor (\neg P \land Q)\).
sur les propositions :
- \(P\) : sportifs qui font du rugby
- \(Q\) : sportifs en catégorie « junior »
On a donc les conditions :
- \((P \land \neg Q)\) :
(activite="rugby" and categorie!="junior")- \((\neg P \land \neg Q)\) :
(activite!="rugby" and categorie="junior")
La requête SQL pourrait donc s’écrire :
SELECT *
FROM sportifs s
WHERE (activite="rugby" and categorie!="junior")
OR (activite!="rugby" and categorie="junior");
Traduisez en propositions et implication la phrase suivante :
- « Si l’accusé est coupable il n’a pas d’alibi. »
Faites la table de vérité correspondant et interpréter tous les cas.
Votre réponse :
Zone de saisie de texte
| Clavier | Action |
|---|---|
| F1 | Afficher une aide technique |
| F2 | Afficher une aide pédagogique |
| Ctrl-A | Tout sélectionner |
| Ctrl-C | Copier la sélection dans le presse-papier |
| Ctrl-V | Copier le presse-papier dans la sélection |
| Ctrl-X | Couper la sélection et la copier dans le presse-papier |
| Ctrl-Z | Annuler la modification |
| Maj-Ctrl-Z | Rétablir la modification |
| Menu | Action |
|---|---|
| Ré-initialiser les sorties | |
| Faire apparaître le menu d'aide | |
| Valider la zone de saisie | |
| Initialiser la zone de saisie | |
| Charger le contenu d'un fichier dans la zone de saisie | |
| Sauvegarder le contenu de la zone de saisie dans un fichier | |
| Imprimer le contenu de la zone de saisie |
Une solution possible :
de la phrase : « Si l’accusé est coupable il n’a pas d’alibi. »
nous pouvons établir les propositions suivantes :
- \(P\) : « l’accusé est coupable »
- \(Q\) : « il n’a pas d’alibi »
Et donc l’implication : SI \(P\) ALORS \(Q\)
En représentant la table de vérité de l’implication :
Implication P Q P => Q 0 0 1 0 1 1 1 0 0 1 1 1
On peut interpréter les différents cas :
- \(P,Q\) sont toutes deux fausses : l’accusé n’est pas coupable et il a un alibi (ç’est classique !)
- \(P\) fausse, \(Q\) vraie : l’accusé n’est pas coupable et il n’a pas d’alibi (ça arrive !)
- \(P\) vraie, \(Q\) fausse : l’accusé est coupable et il a un alibi (ce n’est pas possible, l’alibi ment !)
- \(P\) vraie, \(Q\) vraie : l’accusé est coupable et il n’a pas d’alibi (c’est normal !)
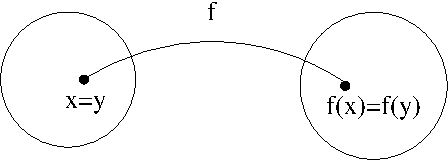
Une application injective se définit par l’implication :
- \(f(x)=f(y) \Rightarrow x=y\)
Vérifiez à l’aide de propositions, de table de vérité de l’implication et de diagrammes de Venn représentant les différents cas sur deux éléments \((x,y)\) que cette définition correspond bien à celle d’une application injective.
Que faudrait-il ajouter dans les diagrammes de Venn des 4 cas possibles pour qu’aucun de ces cas ne puisse être une application surjective ?
De la même manière, montrez que la contraposée de cette implication correspond également bien à la définition d’une application injective.
De la même manière, montrez que la réciproque de cette implication ne correspond pas à la définiton d’une application injective.
Votre réponse :
Zone de saisie de texte
| Clavier | Action |
|---|---|
| F1 | Afficher une aide technique |
| F2 | Afficher une aide pédagogique |
| Ctrl-A | Tout sélectionner |
| Ctrl-C | Copier la sélection dans le presse-papier |
| Ctrl-V | Copier le presse-papier dans la sélection |
| Ctrl-X | Couper la sélection et la copier dans le presse-papier |
| Ctrl-Z | Annuler la modification |
| Maj-Ctrl-Z | Rétablir la modification |
| Menu | Action |
|---|---|
| Ré-initialiser les sorties | |
| Faire apparaître le menu d'aide | |
| Valider la zone de saisie | |
| Initialiser la zone de saisie | |
| Charger le contenu d'un fichier dans la zone de saisie | |
| Sauvegarder le contenu de la zone de saisie dans un fichier | |
| Imprimer le contenu de la zone de saisie |
Une solution possible :
de l’implication : \(f(x)=f(y) \Rightarrow x=y\)
nous pouvons établir les propositions suivantes :
- \(P \; : \; f(x)=f(y)\)
- \(Q \; : \; x=y\)
et représenter la table de vérité :
Implication P Q P => Q 0 0 1 0 1 1 1 0 0 1 1 1
On peut alors interpréter les différents cas :
\(P,Q\) sont toutes deux fausses : les images et les antécédents sont différents
\(P\) fausse, \(Q\) vraie : les images sont différentes pour un même antécédent
\(P\) vraie, \(Q\) fausse : les images sont les mêmes pour deux antécédents différents
\(P\) vraie, \(Q\) vraie : les images sont les mêmes pour le même antécédent
Il n’y a que le troisème cas qui sera faux si l’application est injective.
On a donc bien : \(f(x)=f(y) \Rightarrow x=y\)
La définition d’une application surjective étant que tout élément de l’ensemble d’arrivée doit avoir au moins un antécédent dans l’ensemble de départ, il suffirait donc d’ajouter une image sans antécédent dans l’ensemble d’arrivée pour éviter la possibilité d’avoir une application surjective.
La contraposée de l’implication :
- \(f(x)=f(y) \Rightarrow x=y\)
est :
- \(x \; !=y \Rightarrow f(x) \; !=f(y)\)
nous pouvons établir les propositions suivantes :
- \(P \; : \; x \; !=y\)
- \(Q \; : \; f(x) \; !=f(y)\)
\(P,Q\) sont toutes deux fausses : les images et les antécédents sont égaux
\(P\) fausse, \(Q\) vraie : pour un même antécédent les images sont différentes
\(P\) vraie, \(Q\) fausse : pour deux antécédents différents les images sont les mêmes
\(P\) vraie, \(Q\) vraie : pour deux antécédents différents les images sont différentes
Dans ce cas l’application pourrait être injective, surjective ou bijective
Il n’y a toujours que le troisième cas qui sera faux si l’application est injective.
On a donc bien l’équivalence logique :
- \(x!=y \Rightarrow f(x)!=f(y) \Leftrightarrow f(x)=f(y) \Rightarrow x=y\)
La contraposée de l’implication est équivalent logiquement à l’implication.
La réciproque de l’implication :
- \(f(x)=f(y) \Rightarrow x=y\)
est :
- \(x=y \Rightarrow f(x)=f(y)\)
nous pouvons établir les propositions suivantes :
- \(P \; : \; x=y\)
- \(Q \; : \; f(x)=f(y)\)
\(P,Q\) sont toutes deux fausses : les antécédents et les images sont différents
\(P\) fausse, \(Q\) vraie : pour deux antécédents différents les images sont les mêmes
\(P\) vraie, \(Q\) fausse : pour un même antécédent les images sont différentes
\(P\) vraie, \(Q\) vraie : pour un même antécédent les images sont les mêmes
Si la réciproque de l’implication était logiquement équivalente à cette définition d’une application injective, seul le troisième cas devrait être faux.
La réciproque de l’implication n’est pas équivalente logiquement à l”implication.
On considère la table :
sportifs(nom,age,activite,categorie)On souhaite vérifier que, dans la base de données, les sportifs ayant plus de 18 ans sont inscrits en catégorie « senior » et, par conséquent, s’ils ont moins de 18 ans ne sont pas inscrits dans cette catégorie.
Proposez une requête qui permet de récupérer les sportifs qui ne satisferaient pas ce critère.
Exprimer la requête permettant de trouver les sportifs qui satisfont ce critère à partir de la négation de la proposition précédente.
Montrer que ce dernier critère signifie qu’avoir plus de 18 ans est logiquement équivalent à être inscrit en catégorie « senior ».
Votre réponse :
Une solution possible :
la requête SQL ci-dessous permettra de retrouver les sportifs qui auraient plus de 18 ans et ne seraient pas inscrits en catégorie « senior » et, en cas de problème d’inscription, les sportifs qui auraient moins de 18 ans et auraient été inscrits en catégorie « senior ».
SELECT *
FROM sportifs
WHERE (age >18 AND categorie!="senior") OR (age <= 18 AND categorie="senior");
La négation de la condition de cette requête nous retournera les informations sur les sportifs qui ont plus de 18 ans et qui sont bien inscrits en catégorie « senior » :
SELECT *
FROM sportifs
WHERE (age <=18 OR categorie="senior") AND (age > 18 OR categorie!="senior");
A partir des propositions :
- p : \(age > 18\)
- q : \(categorie="senior"\)
et de l’équivalence logique de l’implication :
- \((p \Rightarrow q) \Leftrightarrow (\neg p \lor q)\)
et de l’équivalence logique de l’équivalence logique :
- \((p \Leftrightarrow q) \Leftrightarrow (p \Rightarrow q \land q \Rightarrow q)\)
On peut vérifier que (équivalence logique de l’implication) :
- \((p \Rightarrow q)\) : \((age >18 \Rightarrow categorie="senior") \Leftrightarrow (age \leq 18 \lor categorie="senior")\)
- \((q \Rightarrow p)\) : \((categorie="senior" \Rightarrow age >18) \Leftrightarrow (categorie!="senior" \lor age > 18 )\)
Et donc que le critère de restriction de la clause WHERE de la requête précédente revient exprimer l’équivalence logique de l’équivalence logique (\((p \Leftrightarrow q) \Leftrightarrow (p \Rightarrow q \land q \Rightarrow q)\)) :
- \((age > 18) \Leftrightarrow (categorie="senior")\)
Par conséquent :
- avoir plus de 18 ans est logiquement équivalent à être inscrit en catégorie « senior »
puisque l’on a vérifié :
- \((age >18 \Rightarrow categorie="senior") \land (categorie="senior" \Rightarrow age >18)\)
Autrement dit avoir plus de 18 ans est logiquement équivalent à être inscrit en catégorie « senior ». Ce qui revient à dire que si les sportifs on plus de 18 ans alors ils sont en catégorie « senior » et que s’ils sont en catégorie « senior » alors ils doivent avoir plus de 18 ans.
Nous pouvons donc formuler la requête SQL ci-dessous pour répondre à cette question.
SELECT *
FROM sportifs
WHERE (age<=18 OR categorie="senior") AND (categorie!="senior" OR age>18);
Au fait c’était quoi la question ?
Ceci dit, cette requête aurait pu simplement être exprimée par la recherche :
- trouver les sportifs qui ont plus de 18 ans et sont seniors ou ceux qui, s’ils ont moins de 18 ans, ne sont pas seniors
qui s’exprimera en SQL par la requête ci-dessous :
SELECT *
FROM sportifs
WHERE (age>18 AND categorie="senior") OR (age<=18 AND categorie!="senior");
On peut vérifier que les deux requêtes ci-dessus sont équivalentes, toujours à partir des propositions :
- p : \(age > 18\)
- q : \(categorie="senior"\)
Et en utilisant l’équivalence logique :
- \((\neg p \lor q) \land (\neg q \lor p) \Leftrightarrow (p \land q) \lor (\neg p \land \neg q)\)
Qu’il suffit de prouver !
Le lecteur pourra vérifier cette équivalence logique en établissant les tables de vérités des deux formules définies dans cette équivalence logique.
On pourra également utiliser les propriétés de l’algèbre de Boole, notamment les lois de distributivité des connecteurs logiques et les propriétés de l’élément neutre de la conjonction (\(\land\)) et de la complémentarité de la disjonction (\(\lor\)) .
Lois de la distributivité des connecteurs logiques :
- \(p \lor (q \land r) = (p \lor q) \land (p \lor r)\)
- \(p \land (q \lor r) = (p \land q) \lor (p \land r)\)
appliquées à la formule :
- \((p \land q) \lor (\neg p \land \neg q)\)
on trouve :
- \(((p \lor \neg p) \land (p \lor \neg q)) \land ((q \lor \neg p) \land (q \lor \neg q))\)
A partir des propriétés de :
- complémentarité de la disjonction : \(p \lor \neg p = 1\)
- élément neutre de la conjonction : \(p \land 1 = p\)
la formule précédente devient :
- \((p \lor \neg q) \land (q \lor \neg p)\)
On en vérifie donc bien l’équivalence logique :
- \((\neg p \lor q) \land (\neg q \lor p) \Leftrightarrow (p \land q) \lor (\neg p \land \neg q)\)