Fichier de rejeu Close
Indication Close
A propos de... Close
Commentaire Close
Systèmes d'Information
- Notions mathématiques
- Calcul relationnel
- Algèbre relationnelle
- Langage de requêtes
- Arbre de requêtes
- Exercices
- Introduction
- Commandes de bases
- Langage de définition de données (LDD)
- Langage de manipulation de données (LMD)
- Types de données
- Exercice
- Dépendances fonctionnelles
- Décomposition de relations
- Inférence logique
- Normalisation
- Aux pays des bières
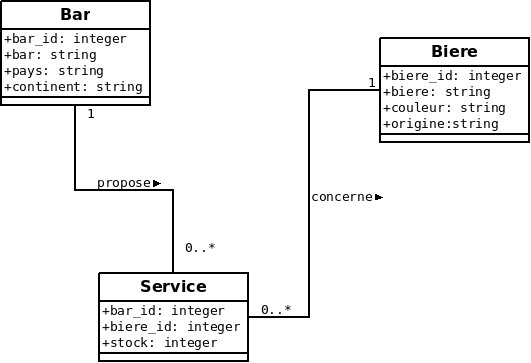
- Modélisation
- Exercices

© Your Copyright
Aide
Division relationnelle
Calcul relationnel
- \(\div(S,T)\), opérateur de l’algèbre relationnelle qui sert à répondre aux questions du type :
- « Trouve-moi les \((X)\) des éléments \((X,Y)\) d’un ensemble \(S\) qui sont en relation avec tous éléments \((Y)\) d’un ensemble \(T\)«
- Exemple :
- » donne-moi les bars \((id\_bar)\) qui servent \((id\_bar,id\_biere)\) toutes les bières \((id\_biere)\) existantes dans la base de données »
On utilisera le quantificateur universel (\(\forall\))
Une solution possible :
- De manière générale :
- \(\div(S,T)=\{x \; | \; \forall y \in T, (x,y) \in S \}\)
- Sur le modèle « bars qui servent des bières » :
- \(\div(Services,Bieres)=\{id\_bar \; | \; \forall id\_biere \in Bieres,(id\_bar,id\_biere) \in Services \}\)
Algèbre relationnelle
La division relationnelle entre l’ensemble \(S(X,Y)\) contenant les groupes d’attributs \((X,Y)\) et l’ensemble \(T(Y)\) contenant le groupe d’attributs \((Y)\) peut s’exprimer à l’aide des opérateurs de base (\(\Pi,\setminus,\times\)) :
\(\div(S,T) = \setminus(\Pi_{(X)}(S),\Pi_{(X)}(\setminus(\times(\Pi_{(X)}(S),T),S)))\)
Qui se décompose de la façon suivante :
- \(R_1=\Pi_{(X)}(S)\) : éléments de l’ensemble \(S\) projetés sur \(X\)
- \(R_2=\times (R_1,T)\) : créer toutes les combinaisons (relations) possibles entre chaque élément (\(X\)) de \(S\) et tous les éléments (\(Y\)) de l’ensemble \(T\)
- \(R_3=\setminus(R_2,S)\) : récupérer les éléments \((X,Y)\) de l’ensemble précédent qui ne seraient pas dans l’ensemble \(S(X,Y)\)
- \(R_4=\Pi_{(X)}(R_3)\) : récupérer seulement les \(X\) de l’ensemble précédent qui ne seraient pas en relation avec ceux de l’ensemble \(S(X,Y)\)
- \(\div(S,T) =\setminus(R_1,R_4)\) : la différence entre les \(X\) de \(S\) et les \(X\) de l’ensemble précédent donnera, s’ils existent, les \(X\) de l’ensemble \(S(X,Y)\) liés à tous les \(Y\) de l’ensemble \(T(Y)\)
On peut également interpréter cette formulation en deux phases :
- créer un ensemble qui contiendrait les éléments \(X\) associés aux éléments \(T(Y)\) qui ne seraient pas liés aux éléments \(X\) de l’ensemble \(S(X,Y)\) :
- \(E_1=\Pi_{(X)}(\setminus(\times(\Pi_{(X)}(S),T),S))\)
- récupérer les \(X\) de l’ensemble \(S\) et faire la différence avec les éléments \(X\) de l’ensemble précédent : on obtient les \(X\) de l’ensemble \(S\) qui sont liés à tous les éléments de l’ensemble \(T\) :
- \(\div(S,T)=\setminus(\Pi_{(X)}(S),E_1)\)
Formulation SQL
- La division relationnelle peut-être représentée de différentes manières en SQL.
- en l’exprimant à l’aide des opérateurs de base (\(\Pi,\times,\setminus\))
- en l’exprimant par des requêtes imbriquées (
NOT EXISTSet/ouEXCEPT) - en utilisant des groupements et fonctions d’agrégat (
GROUP BY, HAVING,COUNT)
- Mise en œuvre sur le modèle de données des bars qui servent des bières :
- Trouver les bars qui servent toutes les bières …
| Table « bars » | Table « bieres » | Table « services » | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
- On peut représenter la division relationnelle à l’aide des opérateurs de base :
- \(\Pi\) : projection
- \(\times\) : produit cartésien
- \(\setminus\) : différence
- à partir de l’expression suivante :
- \(\setminus(\Pi_{(X)}(S),\Pi_{(X)}(\setminus(\times(\Pi_{(X)}(S),T),S)))\)
- Dans le cas des « bars qui servent toutes les bières » cela revient à :
- créer un ensemble qui contiendrait les bars qui ne serviraient pas certaines bières
- \(R_1=\setminus(\Pi_{(id\_bar,id\_biere)}(\times(services,bieres)),\Pi_{(id\_bar,id\_biere)}(services))\)
- récupérer l’ensemble des bars qui servent des bières
- \(R_2=\Pi_{(id\_bar)}(services)\)
- faire la différence entre les deux ensembles :
- \(R=\setminus(R_2,\Pi_{(id\_bar)}(R_1))\)
On récupère ainsi les bars qui servent toutes les bières.
Mise en œuvre :
Créer un vue SQL pour « rechercher les bars qui ne serviraient pas certaines bières ».
Votre réponse :
Une solution possible :
- On traduit directement en SQL la requête algébrique :
- \(\setminus(\Pi_{(id\_bar,id\_biere)}(\times(services,bieres)),\Pi_{(id\_bar,id\_biere)}(services))\)
Rechercher les bars qui serviraient toutes les bières existantes dans la base de données.
Votre réponse :
Une solution possible :
- On utilise la vue créée dans la question précédente :
- \(R_1=\setminus(\Pi_{(id\_bar,id\_biere)}(\times(services,bieres)),\Pi_{(id\_bar,id\_biere)}(services))\)
- On récupère les bars (\(id\_bar\)) qui servent (\(services\)) des bières (\(id\_biere\)) et on fait la différence avec « bars qui ne serviraient pas certaines bières »
- \(R=\setminus(\Pi_{(id\_bar)}(services),\Pi_{(id\_bar)}(R_1))\)
On récupère donc les bars qui servent toute les bières.
On peut représenter la division relationnelle par une requête imbriquée (NOT EXISTS) avec une opération ensembliste de différence (EXCEPT).
SELECT se.X
FROM S se
WHERE NOT EXISTS (
(SELECT Y FROM T)
EXCEPT
(SELECT Y FROM S si WHERE si.X=se.X)
);
- Ce qui se traduit par :
- « récupérer les \(X\) de \(S\) pour lesquels la différence entre les \(Y\) de \(T\) et ceux de \(S\) est nulle »
On peut aussi représenter la division relationnelle par une double négation (NOT EXISTS).
SELECT se.X
FROM S se
WHERE NOT EXISTS ( SELECT *
FROM T
WHERE NOT EXISTS (SELECT *
FROM S si
WHERE si.X=se.X AND T.Y=si.Y)
);
- Ce qui se traduit par :
- – trouver les \(X\) de \(S\) tel qu’il n’existe pas de \(T\) pour lesquels il n’existe pas de \(S\) associés à ce \(T\)
Mise en œuvre :
Ecrire la requête SQL pour retrouver » les bars qui servent toutes les bières » à l’aide des opérateurs (NOT EXISTS,EXCEPT)
Votre réponse :
Une solution possible :
Ecrire la requête SQL pour retrouver » les bars qui servent toutes les bières » à l’aide de l’opérateur (NOT EXISTS)
Votre réponse :
Une solution possible :
On peut aussi exprimer la division relationnelle en SQL en utilisant des groupements et fonction d’agrégat.
SELECT X
FROM S
GROUP BY X
HAVING COUNT(DISTINCT Y)=(
SELECT COUNT(DISTINCT Y)
FROM T
);
- Ce qui se traduit par :
- « récupérer les \(X\) de \(S\) pour lesquels le nombre total de \(Y\) est égal au nombre de \(Y\) de \(T\)«
Attention : compter le nombre de Y ne vérifie pas qu’ils sont bien les mêmes.
Mise en œuvre :
Ecrire la requête SQL pour retrouver » les bars qui servent toutes les bières » à l’aide de l’opérateur (NOT EXISTS)
Votre réponse :
Une solution possible :
Exercice récapitulatif
Créer les tables S(X,Y), T(Y) contenant les informations suivantes
table \(S\)
| X | Y |
|---|---|
| 1 | a |
| 2 | b |
table \(T\)
| Y |
|---|
| a |
Votre réponse :
Une solution possible :
A partir des instances de tables :
|
|
||||||||||||
Rechercher les éléments \(X\) de \(S\) qui sont en relation avec tous les éléments \(Y\) de \(T\)
Votre réponse :
Une solution possible :
On met en œuvre les requêtes imbriquées avec NOT EXISTS,EXCEPT ou un double NOT EXISTS
Modifier les instances de tables S,T pour qu’elles contiennent :
|
|
|||||||||||||||
et rechercher à nouveau les éléments \(X\) de \(S\) qui sont en relation avec tous les éléments \(Y\) de \(T\). Justifiez-le résultat obtenu.
Votre réponse :
Une solution possible :
On obtient un ensemble vide car il n’y a pas un même élément X
associé à tous les X de T.
En effet, l’élément (1) de X est bien associé à l’élément (a) de Y
mais c’est l’élément (2) de X qui est associé à l’élément (c) de Y.
Modifier à nouveau les instances de tables S,T pour qu’elles contiennent :
|
|
|||||||||||||||||
et rechercher à nouveau les éléments \(X\) de \(S\) qui sont en relation avec tous les éléments \(Y\) de \(T\) à l’aide de requêtes imbriquées.
Votre réponse :
Une solution possible :
A partir des instances de tables S,T essayez de mettre en oeuvre la division relationnelle
avec groupement et fonctions d’agrégats. Justifiez le résultat obtenu.
|
|
|||||||||||||||||
Votre réponse :
Une solution possible :
Nous n’obtenons pas le bon résultat car il y a des doublons sur la colonne Y de la table S.
Le groupement sur la colonne X donnera donc un nombre de Y associés qui peut très bien être
égal au nombre de Y de l’ensemble T sans les contenir tous.