Fichier de rejeu Close
Indication Close
A propos de... Close
Commentaire Close
Systèmes d'Information
- Notions mathématiques
- Calcul relationnel
- Algèbre relationnelle
- Langage de requêtes
- Arbre de requêtes
- Exercices
- Introduction
- Commandes de bases
- Langage de définition de données (LDD)
- Langage de manipulation de données (LMD)
- Types de données
- Exercice
- Dépendances fonctionnelles
- Décomposition de relations
- Inférence logique
- Normalisation
- Aux pays des bières
- Modélisation
- Exercices
© Your Copyright
Aide
Injection
Nous présentons ici la définition d’une injection entre deux ensembles sous forme de :
- définition mathématique
- cardinalité d’une relation injective
- diagramme sagittal
- modèle Entité-Association
- modélisation UML
puis nous illustrons cette notion mathématique sur un exemple simple d’un ensemble d’employés et de sociétés.
Une relation binaire applicative \(f\) est une injection si et seulement si :
- \(\forall (x,y) \in (E \times E), f(x)=f(y) \Rightarrow x=y\)
Ou sa contraposée :
- \(\forall (x,y) \in E \times E, x \neq y \Rightarrow f(x) \neq f(y)\)
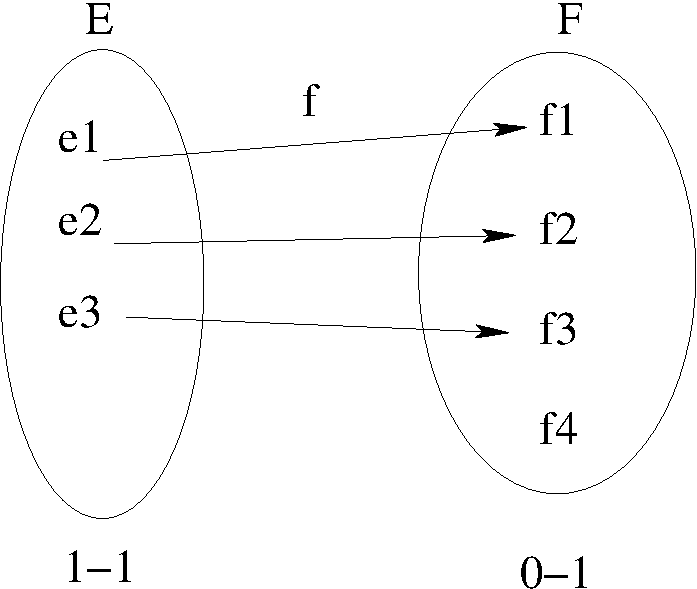
Autrement dit, une application injective \(f\) d’un ensemble \(E\) vers un ensemble \(F\) notée :
\[f : E \rightarrow F\]\[ x \mapsto f(x)\]est une relation binaire de \(E\) vers \(F\) pour laquelle :
- chaque élément de \(F\) possède au plus un antécédent dans l’ensemble \(E\)
c’est-à-dire, 2 éléments distincts de \(E\) ont 2 images distinctes dans \(F\)
- \((1-1)\) : chaque élément de \(E\) est en relation avec un et un seul élément de \(F\).
- \((0-1)\) : les éléments de \(F\) peuvent être en relation avec au plus un élément de \(E\).
Le diagramme sagittal ci-dessous représente un exemple de relation injective.
Les cardinalités de l’application injective sont représentées sous les ensembles \(E,F\).
La répresentation d’une application injective dans un modèle Entité-Assocation se représente avec le formalisme ci-dessous :
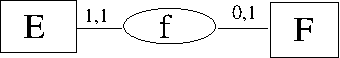
On remarquera que dans le formalisme E-A les notations sont très similaires :
- le positionnement des cardinalités est du même côté (des entités au lieu des ensembles)
- la notation des cardinalités (\(1,1\) et \(0,1\)) correspond aux notations (\(1-1\) et \(0-1\))
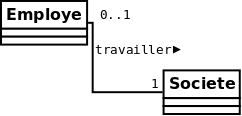
La répresentation d’une application injective dans un modèle UML se représente avec le formalisme ci-dessous :
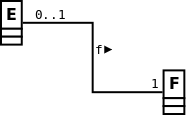
On remarquera que dans le formalisme UML les notations sont différentes :
le positionnement des cardinalités est inversé par rapport au diagramme sagittal
la notation UML (\(1\)) correspond à la notation (\(1-1\)) :
- un et un seul (\(-1\)) élément de \(F\) est en relation avec chaque (\(1-\)) élément de \(E\).
la notation UML (\(0..1\)) correspond à la notation (\(0-1\)) :
- un élément de \(F\) peut, ou pas (\(0..\)), être en relation avec au plus (\(..1\)) élément de \(E\).
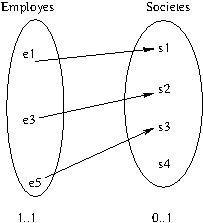
On veut modéliser un système d’information qui permettrait de gérer des employés dans des sociétés.
Dans cette injection on veut exprimer les contraintes suivantes sur les employés et les sociétés :
- chaque employé travaille dans une seule société.
- une société ne peut avoir au plus qu’un employé
- \((1-1)\) : chaque
Employétravaille dans une seuleSociété. - \((0-1)\) : les
Sociétéauront au plusEmployé.
Les contraintes de la relation Employé-Société sont celles d’une application injective que l’on peut illustrer avec l’exemple de
diagramme sagittal ci-dessous :
La répresentation de l’application injective Employé-Société dans le formalisme Entité-Assocation :
La répresentation de l’application injective Employé-Société dans le formalisme UML :
