Fichier de rejeu Close
Indication Close
A propos de... Close
Commentaire Close
Téléchargements

Aide
Itération - Exercices de programmation
-
Décodeur logique
On considère le circuit logique ci-dessous où \(a\), \(b\) et \(c\) sont les entrées et \(s_0, s_1, \ldots, s_7\) les sorties.
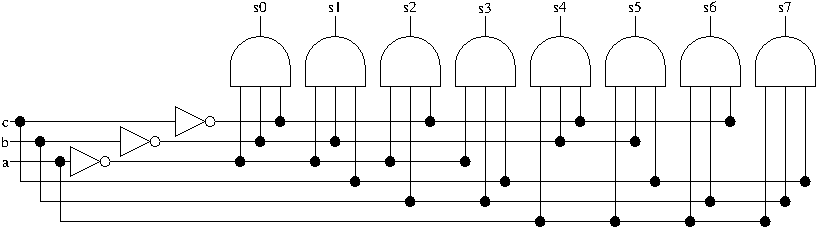
Proposer un algorithme qui affiche la table de vérité du circuit à l'aide d'itérations conditionnelles.
opérateurs booléens

 aide Python
aide Pythonitération conditionnelle (documentation Python)
while condition : blocWhile
opérateurs booléens (documentation Python)
not anégation : \(\overline{a}\)
a and bconjonction : \(a\cdot b\)
a or bdisjonction : \(a + b\)
Votre réponse :
AAV2_ITE: Méthode
Définir les 4 caractéristiques de la méthode de l'invariant dans le cas particulier de l'énoncé.
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie AAV5_ITE: Résultat
Utiliser l'interpréteur Python ci-dessous pour programmer l'algorithme demandé.
python : essai.pyOutputAAV3_ITE: Vérification
Appliquer cette technique au résultat proposé.
Si la technique proposée nécessite Python, on la mettra en œuvre dans l'interpréteur ci-dessus (cf. Résultats).
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie
Une solution possible :
AAV2_ITE: Choisir et appliquer une méthode générique
On utilise une représentation analytique. En effet, lorsque un objet est représenté sous une forme graphique, il est préférable de le transformer en sa représentation analytique (lorsqu'elle existe) pour étudier cet objet à l'aide d'un programme informatique.
Le circuit logique de l'énoncé a 3 entrées \(a\), \(b\) et \(c\) et 8 sorties \(s_0, s_1, \ldots, s_7\) telles que:
# description du circuit s0 = not a and not b and not c s1 = not a and not b and c s2 = not a and b and not c s3 = not a and b and c s4 = a and not b and not c s5 = a and not b and c s6 = a and b and not c s7 = a and b and c
Il faut 3 boucles imbriquées pour explorer les \(2^3 = 8\) combinaisons possibles en entrée:
a = 0 while not a > 1 : b = 0 while not b > 1 : c = 0 while not c > 1 : # description du circuit # ... # affichage des résultats c = c + 1 b = b + 1 a = a + 1
AAV5_ITE: Répondre explicitement à la question posée
Le code Python qui établit la table de vérité du circuit est présenté ci-dessous.
python : iteration-type-boolean.pyOutputAAV3_ITE: Choisir et appliquer une technique de vérification
On établit par un calcul « à la main » la table de vérité` du circuit proposé et on vérifie bien que le code Python précédent donne le même résultat.
On pourrait également utiliser le simulateur de circuits logiques ci-dessous pour établir la table de vérité du circuit.
Circuit logique : iteration-decodeur.jsonEntrées/Sorties
Portes 1/1
Portes 2/1
Portes 3/1
Vue d'ensemble On constate que ce circuit réalise un décodage des entrées vers une seule sortie : pour chaque combinaison des entrées, une seule sortie est activée et jamais la même.
-
Conversion décimal/binaire
Proposer un algorithme qui code un entier décimal \(n\) en base \(b = 2\). Le nombre binaire sera codé sous forme d'une chaîne de caractères composée de 0 et de 1.
Exemples :
décimal binaire 2 "10"5 "101"13 "1101"23 "10111"128 "10000000"numération en base bUn entier \(n\) en base \(b\) est représenté par une suite de chiffres \((r_mr_{m-1}\ldots r_1r_0)_b\) où les \(r_i\) sont des chiffres de la base \(b\) (\(0\leq r_i < b\)). Ce nombre \(n\) a pour valeur :
\[n = r_mb^m + r_{m-1}b^{m-1} + \ldots + r_1b^1 + r_0b^0 = \sum^{i=m}_{i = 0} r_ib^i\]L'algorithme de conversion en base \(b\) consiste à diviser successivement le nombre \(n\) par la base \(b\) (\(n = bq + r\)) tant que le quotient \(q\) n'est pas nul. L'ordre inverse des restes \(r_i\) des différentes divisions (du dernier au premier reste, écrits de gauche à droite) donne la représentation du nombre \(n\) en base \(b\).
\[\begin{array}{lll} n &=& q_0b + r_0 = q_0b^1 + {r_0b^0}\\ n &=& (q_1b^1 + r_1)b^1 + r_0b^0 = q_1b^2 + {r_1b^1 + r_0b^0} \\ n &=& (q_2b^1 + r_2)b^2 + r_1b^1 + r_0b^0 = q_2b^3 + {r_2b^2 + r_1b^1 + r_0b^0}\\ n &=& \ldots\\ n &=& 0\cdot b^{m+1} + {r_mb^m + \ldots + r_2b^2 + r_1b^1 + r_0b^0} = \displaystyle \sum^{i=m}_{i = 0} r_ib^i\\ n &=& (r_mr_{m-1}\ldots r_1r_0)_b \end{array}\]aide Pythonitération conditionnelle (documentation Python)
while condition : blocWhile
opérateurs arithmétiques (documentation Python)
x/yquotient de la division entière si arguments entiers : \(x\div y\), division réelle sinon : \(x/y\).
x%yreste de la division entière : \(x\mod y\).
x**nélévation à la puissance : \(x^n\).
Votre réponse :
AAV2_ITE: Méthode
Définir les 4 caractéristiques de la méthode de l'invariant dans le cas particulier de l'énoncé.
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie AAV5_ITE: Résultat
Utiliser l'interpréteur Python ci-dessous pour programmer l'algorithme demandé.
python : essai.pyOutputAAV3_ITE: Vérification
Appliquer cette technique au résultat proposé.
Si la technique proposée nécessite Python, on la mettra en œuvre dans l'interpréteur ci-dessus (cf. Résultats).
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie
Une solution possible :
AAV2_ITE: Choisir et appliquer une méthode générique
On utilise la méthode de l'invariant pour concevoir la boucle qui va réaliser les divisions successives, l'ordre inverse des restes des différentes divisions (du dernier au premier reste, écrits de gauche à droite) donnant la représentation du nombre, en précisant les 4 caractéristiques de la méthode : initialisation, invariant, condition d'arrêt, progression.
Méthode de l'invariant Codage binaire initialisation q, r = n/b, n%b ; code = str(r)invariant à chaque étape k: \(\displaystyle code = \sum_{i=0}^k r_i2^i\)condition d'arrêt q == 0progression insérer le nouveau reste dans le code avant de re-diviser le quotient par b boucle q, r = n/b, n%b code = str(r) while q != 0 : r = q%b code = str(r) + code q = q/b
AAV5_ITE: Répondre explicitement à la question posée
Le code Python de codage en base
best présenté ci-dessous.python : iteration-type-number.pyOutputAAV3_ITE: Choisir et appliquer une technique de vérification
On propose un jeu de tests pour vérifier le codage obtenu. On utilise pour cela les 5 exemples de couples entrées-sorties de l'énoncé.
Le programme Python retrouve bien les 5 exemples donnés dans l'énoncé.
-
Dessin d'étoiles
Proposer un algorithme qui dessine la figure ci-dessous composée de l'« étoile »
*(astérisque):********** **** **** *** *** ** ** * *
aide Pythonitération conditionnelle (documentation Python)
while condition : blocWhile
opérateurs de séquences (documentation Python)
x in sTruesixappartient à la séquences,Falsesinon.x not in sFalsesixappartient à la séquences,Truesinon.s + tconcaténation (mise bout à bout) de
sett.n*sconcaténation de
savec elle-même,nfois.s[i]élément de rang
i+1dans la séquences(le premier élément a pour rang 0).s[i:j]séquence formée des éléments de la séquence
sdes rangsiinclus àjexclu.len(s)nombre d'éléments (longueur) de la séquence
s.
Votre réponse :
AAV2_ITE: Méthode
Définir les 4 caractéristiques de la méthode de l'invariant dans le cas particulier de l'énoncé.
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie AAV5_ITE: Résultat
Utiliser l'interpréteur Python ci-dessous pour programmer l'algorithme demandé.
python : essai.pyOutputAAV3_ITE: Vérification
Appliquer cette technique au résultat proposé.
Si la technique proposée nécessite Python, on la mettra en œuvre dans l'interpréteur ci-dessus (cf. Résultats).
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie
Une solution possible :
AAV2_ITE: Choisir et appliquer une méthode générique
On utilise la méthode de l'invariant pour concevoir la boucle qui va dessiner les lignes successives, en précisant les 4 caractéristiques de la méthode : initialisation, invariant, condition d'arrêt, progression.
Méthode de l'invariant Dessin d'étoiles initialisation n, blancs = 5, 0 ligne = (n-blancs)*'*' + 2*blancs*' ' + (n-blancs)*'*'
invariant à chaque étape ligne == (n-blancs)*'*' + 2*blancs*' ' + (n-blancs)*'*'condition d'arrêt blancs == nprogression insérer un blancde chaque côtéboucle n, blancs = 5, 0 ligne = (n-blancs)*'*' + 2*blancs*' ' + (n-blancs)*'*' while blancs < n : print ligne blancs = blancs + 1 ligne = (n-blancs)*'*' + 2*blancs*' ' + (n-blancs)*'*'
AAV5_ITE: Répondre explicitement à la question posée
Le code Python de ce dessin d'étoiles est présenté ci-dessous.
python : iteration-type-string.pyOutputAAV3_ITE: Choisir et appliquer une technique de vérification
Une simple comparaison de figures suffit ici : le programme Python redonne bien la figure de l'énoncé.
-
Palindrome
Proposer un algorithme qui teste si un n-uplet est un palindrome.
Exemples de n-uplets palindromes:
(1,2,3,3,2,1) ('n','o','n') ('k','a','y','a','k') ([],[1],[2,3],[4,5,6],[2,3],[1],[])
aide Pythonitération conditionnelle (documentation Python)
while condition : blocWhile
opérateurs de séquences (documentation Python)
x in sTruesixappartient à la séquences,Falsesinon.x not in sFalsesixappartient à la séquences,Truesinon.s + tconcaténation (mise bout à bout) de
sett.n*sconcaténation de
savec elle-même,nfois.s[i]élément de rang
i+1dans la séquences(le premier élément a pour rang 0).s[i:j]séquence formée des éléments de la séquence
sdes rangsiinclus àjexclu.len(s)nombre d'éléments (longueur) de la séquence
s.
Votre réponse :
AAV2_ITE: Méthode
Définir les 4 caractéristiques de la méthode de l'invariant dans le cas particulier de l'énoncé.
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie AAV5_ITE: Résultat
Utiliser l'interpréteur Python ci-dessous pour programmer l'algorithme demandé.
python : essai.pyOutputAAV3_ITE: Vérification
Appliquer cette technique au résultat proposé.
Si la technique proposée nécessite Python, on la mettra en œuvre dans l'interpréteur ci-dessus (cf. Résultats).
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie
Une solution possible :
AAV2_ITE: Choisir et appliquer une méthode générique
On utilise la méthode de l'invariant pour concevoir la boucle qui va tester 2 à 2 les éléments du n-uplets, en précisant les 4 caractéristiques de la méthode : initialisation, invariant, condition d'arrêt, progression.
Méthode de l'invariant Palindrome initialisation rang, palindrome = 0, True
invariant à chaque étape k,p[k]représente le \(k^{\grave eme}\) élément de la listep.condition d'arrêt rang == len(p)/2 or palindromeprogression comparer p[rang]àp[len(p)-1-rang]et avancer d'un élément si ok, sinon arrêter.boucle rang, palindrome = 0, True while rang < len(p)/2 and palindrome : if p[rang] != p[len(p)-1-rang] : palindrome = False else : rang = rang + 1
AAV5_ITE: Répondre explicitement à la question posée
Le code Python qui teste les n-uplets palindromes est présenté ci-dessous.
python : iteration-type-tuple.pyOutputAAV3_ITE: Choisir et appliquer une technique de vérification
On utilise un jeu de tests composé des 4 exemples de l'énoncé et de quelques exemples qui ne sont pas des palindromes.
Le programme Python donne des résultats corrects dans les 4 cas attendus ainsi que dans 3 cas qui ne sont pas des palindromes.
-
Recherche d'un élément
Proposer un algorithme qui trouve le rang de la première occurrence d'un élément au sein d'une liste.
aide Pythonitération conditionnelle (documentation Python)
while condition : blocWhile
opérateurs de séquences (documentation Python)
x in sTruesixappartient à la séquences,Falsesinon.x not in sFalsesixappartient à la séquences,Truesinon.s + tconcaténation (mise bout à bout) de
sett.n*sconcaténation de
savec elle-même,nfois.s[i]élément de rang
i+1dans la séquences(le premier élément a pour rang 0).s[i:j]séquence formée des éléments de la séquence
sdes rangsiinclus àjexclu.len(s)nombre d'éléments (longueur) de la séquence
s.
Votre réponse :
AAV2_ITE: Méthode
- Définir les 4 caractéristiques de la méthode de l'invariant
dans le cas particulier de l'énoncé.
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie
AAV5_ITE: Résultat
Utiliser l'interpréteur Python ci-dessous pour programmer l'algorithme demandé.
python : essai.pyOutputAAV3_ITE: Vérification
Appliquer cette technique au résultat proposé.
Si la technique proposée nécessite Python, on la mettra en œuvre dans l'interpréteur ci-dessus (cf. Résultats).
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie
Une solution possible :
AAV2_ITE: Choisir et appliquer une méthode générique
On utilise la méthode de l'invariant pour concevoir la boucle qui va passer en revue les éléments de la liste un par un jusqu'à trouver l'occurrence recherchée, en précisant les 4 caractéristiques de la méthode : initialisation, invariant, condition d'arrêt, progression.
Méthode de l'invariant Recherche d'un élément initialisation rang, found = 0, False
invariant à chaque étape k,t[k]représente le \(k^{\grave eme}\) élément de la listet.condition d'arrêt rang == len(t) or foundprogression comparer t[rang]à l'élémentxrecherché et avancer d'un élément si pas trouvé, sinon arrêter.boucle rang, found = 0, False while rang < len(t) and not found : if t[rang] == x : found = True else : rang = rang + 1
AAV5_ITE: Répondre explicitement à la question posée
Le code Python de recherche d'un élément est présenté ci-dessous.
python : iteration-type-list.pyOutputAAV3_ITE: hoisir et appliquer une technique de vérification
On utilise un jeu de tests pour vérifier le bon fonctionnement de cet algorithme de recherche.
Au moins 3 cas sont à prévoir :
- l'élément recherché n'est pas dans la liste;
- l'élément recherché n'apparaît qu'une seule fois dans la liste;
- l'élément recherché apparaît plusieurs fois dans la liste.
Le programme Python donne des résultats corrects dans les 3 types de cas attendus :
Pas d'occurrence de
x:1 [7, 9, 4, 5, 0] 5 Falsefoundest àFalse.Une seule occurrence de
x:3 [1, 3, 4, 1, 4] 1 Trueon a bien
t[1] == 3etfound == True.Plusieurs occurrences de
x:2 [7, 1, 2, 2, 0] 2 Truela première occurrence de
2est bien telle quet[2] == 2etfound == True.
-
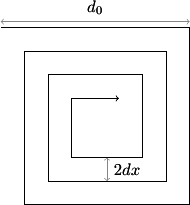
Spirales rectangulaires
Ecrire un algorithme qui trace une spirale rectangulaire de \(n\) côtés dont le côté initial est \(d_0\) et l'accroissement entre deux côtés successifs \(dx\).
 aide Python
aide Pythonitération conditionnelle (documentation Python)
while condition : blocWhile
tortue Logo (documentation Python)
import turtlemodule Python à importer pour manipuler la tortue Logo.
t = turtle.Turtle()crée une tortue
t.t.down()tracer la trajectoire de la tortue Logo.
t.up()ne pas tracer la trajectoire de la tortue Logo.
t.setheading(a)oriente la tortue
tdans une direction qui fait l'anglea(en degrés) avec l'axe horizontal (sens trigonométrique).t.forward(d)fait avancer la tortue
td'une distanceddans la direction courante.t.backward(d)fait reculer la tortue
td'une distanceddans la direction courante.t.left(a)fait tourner sur la gauche (sens trigonométrique) la tortue
t(sans avancer, ni reculer) d'un angleapar rapport à la direction courante.t.right(a)fait tourner sur la droite (sens horaire) la tortue
t(sans avancer, ni reculer) d'un angleapar rapport à la direction courante.t.goto(x,y)fait aller la tortue au point de coordonnées
(x,y)quelle que soit son orientation.
Votre réponse :
AAV2_ITE: Méthode
Définir les 4 caractéristiques de la méthode de l'invariant dans le cas particulier de l'énoncé.
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie AAV5_ITE: Résultat
Utiliser l'interpréteur Python ci-dessous pour programmer l'algorithme demandé.
python : essai.pyOutputAAV3_ITE: Vérification
Appliquer cette technique au résultat proposé.
Si la technique proposée nécessite Python, on la mettra en œuvre dans l'interpréteur ci-dessus (cf. Résultat).
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie
Une solution possible :
AAV2_ITE: Choisir et appliquer une méthode générique
On utilise la méthode de l'invariant pour concevoir la boucle qui va effectuer le suivi de trajectoire d'une spirale rectangulaire, en précisant les 4 caractéristiques de la méthode : initialisation, invariant, condition d'arrêt, progression.
Méthode de l'invariant Spirale rectangulaire initialisation i, d = 0, d0
invariant à chaque étape i, \(d = d_0 + i\cdot dx\)condition d'arrêt i == nprogression avancer de det tourner à angle droit.boucle i, d = 0, d0 while i < n : t.forward(d) t.left(90) d = d + dx i = i + 1
AAV5_ITE: Répondre explicitement à la question posée
Le code Python qui dessine une spirale rectangulaire est présenté ci-dessous.
python : iteration-logo-1.pyOutputAAV3_ITE: Choisir et appliquer une technique de vérification
Une simple comparaison de figures suffit pour constater qu'on obtient effectivement des spirales rectangulaires conformes à l'exemple de l'énoncé.
-
Polygone régulier
Ecrire un algorithme qui trace un polygone régulier de \(n\) côtés de longueur \(d\).
aide Pythonitération conditionnelle (documentation Python)
while condition : blocWhile
tortue Logo (documentation Python)
import turtlemodule Python à importer pour manipuler la tortue Logo.
t = turtle.Turtle()crée une tortue
t.t.down()tracer la trajectoire de la tortue Logo.
t.up()ne pas tracer la trajectoire de la tortue Logo.
t.setheading(a)oriente la tortue
tdans une direction qui fait l'anglea(en degrés) avec l'axe horizontal (sens trigonométrique).t.forward(d)fait avancer la tortue
td'une distanceddans la direction courante.t.backward(d)fait reculer la tortue
td'une distanceddans la direction courante.t.left(a)fait tourner sur la gauche (sens trigonométrique) la tortue
t(sans avancer, ni reculer) d'un angleapar rapport à la direction courante.t.right(a)fait tourner sur la droite (sens horaire) la tortue
t(sans avancer, ni reculer) d'un angleapar rapport à la direction courante.t.goto(x,y)fait aller la tortue au point de coordonnées
(x,y)quelle que soit son orientation.
Votre réponse :
AAV2_ITE: Méthode
Définir les 4 caractéristiques de la méthode de l'invariant dans le cas particulier de l'énoncé.
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie AAV5_ITE: Résultat
Utiliser l'interpréteur Python ci-dessous pour programmer l'algorithme demandé.
python : essai.pyOutputAAV3_ITE: Vérification
Appliquer cette technique au résultat proposé.
Si la technique proposée nécessite Python, on la mettra en œuvre dans l'interpréteur ci-dessus (cf. Résultat).
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie
Une solution possible :
AAV2_ITE: Choisir et appliquer une méthode générique
On utilise la méthode de l'invariant pour concevoir la boucle qui va effectuer le suivi de trajectoire d'un polygone régulier, en précisant les 4 caractéristiques de la méthode : initialisation, invariant, condition d'arrêt, progression.
Méthode de l'invariant Polygone régulier initialisation i = 0
invariant à chaque étape i,icôtés du polygone ont été tracés.condition d'arrêt i == nprogression avancer de det tourner de \((360/n)\) degrés.boucle i = 0 while i < n : t.forward(d) t.left(360./n) i = i + 1
AAV5_ITE: Répondre explicitement à la question posée
Le code Python qui dessine une spirale rectangulaire est présenté ci-dessous.
python : iteration-logo-2.pyOutputAAV3_ITE: Choisir et appliquer une technique de vérification
Une simple comparaison de figures suffit pour constater qu'on obtient effectivement des polygones réguliers.
-
Distribuer les cartes
Distribuer aléatoirement un jeu de 32 cartes à tour de rôle entre 4 joueurs.
aide Pythonitération conditionnelle (documentation Python)
while condition : blocWhile
nombres aléatoires (documentation Python)
import randommodule Python à importer pour manipuler des nombres aléatoires.
random.random()retourne un nombre réel aléatoirement compris entre
0inclus et1exclu.random.randint(min,max)retourne un nombre entier aléatoirement compris entre
minetmaxinclus.listes (documentation Python)
s[i] = xl'élément de rang
ide la listesest remplacé parx.del s[i]l'élément de rang
ide la listesest supprimé; la longueur de la liste diminue d'une unité.s.append(x)xest ajouté à la fin de la listes; la longueur de la liste augmente d'une unité.s.insert(i, x)xest inséré au rangidans la listes; la longueur de la liste augmente d'une unité.range(start=0, stop, step=1)génère la liste des entiers
startinclus (0 par défaut) àstopexclu par pas destep(1 par défaut).
Votre réponse :
AAV2_ITE: Méthode
Définir les 4 caractéristiques de la méthode de l'invariant dans le cas particulier de l'énoncé.
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie AAV5_ITE: Résultat
Utiliser l'interpréteur Python ci-dessous pour programmer l'algorithme demandé.
python : essai.pyOutputAAV3_ITE: Vérification
Appliquer cette technique au résultat proposé.
Si la technique proposée nécessite Python, on la mettra en œuvre dans l'interpréteur ci-dessus (cf. Résultats).
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie
Une solution possible :
AAV2_ITE: Choisir et appliquer une méthode générique
On utilise la méthode de l'invariant pour tirer au sort une carte et la distribuer au bon joueur en précisant les 4 caractéristiques de la méthode : initialisation, invariant, condition d'arrêt, progression.
Les « mains » des joueurs pourront être représentées par des listes de cartes.
Soient :
jeu = range(1,33)le jeu de cartes;j1, j2, j3, j4 = [], [], [], []les « mains » respectives des 4 joueurs, initialement vides;tour = [j1,j2,j3,j4]le tour de table.Méthode de l'invariant Distribuer les cartes initialisation n, joueur = 0, tour[0]
invariant à chaque étape n, la carte enlevée du jeu est celle donnée au joueur courant.condition d'arrêt jeu == [](il n'y a plus de cartes à distribuer)progression tirer une carte du jeu; donner la carte au joueur courant et passer au joueur suivant. boucle n, joueur = 0, tour[0] while jeu != [] : # tirer une carte rang = random.randint(0,len(jeu)-1) carte = jeu[rang] # donner la carte au joueur joueur.append(carte) # supprimer la carte du jeu del jeu[rang] # passer au joueur suivant n = n + 1 joueur = tour[n%4]
AAV5_ITE: Répondre explicitement à la question posée
Le code Python qui distribue les cartes est présenté ci-dessous.
python : iteration-jeux-2.pyOutputAAV3_ITE: Choisir et appliquer une technique de vérification
Une simple comparaison de valeurs suffit : chaque joueur a bien 8 cartes, toutes différentes les unes des autres et différentes de celles des autres joueurs.
-
Classer par couleurs
On ne s'intéresse ici qu'à la couleur d'une carte (pique=0, cœur=1, carreau=2, trèfle=3), pas à sa valeur (1, 2, 3, ..., 10, V, D, R).
On considère une « main » de 7 cartes distribuées aléatoirement. Une main sera représentée par une liste de couleurs.
Exemples de mains:
[2, 0, 3, 2, 1, 2, 0] [0, 3, 1, 3, 1, 1, 0] [2, 1, 0, 2, 3, 3, 2] [2, 2, 3, 2, 2, 1, 3]
Ecrire un algorithme qui classe les cartes d'une « main » par couleurs : tous les piques en premier, tous les cœurs en deuxième, puis les carreaux et enfin les trèfles.
Exemples d'ordonnancements:
avant : [2, 0, 3, 2, 1, 2, 0] après : [0, 0, 1, 2, 2, 2, 3] avant : [0, 3, 1, 3, 1, 1, 0] après : [0, 0, 1, 1, 1, 3, 3] avant : [3, 3, 0, 3, 0, 1, 0] après : [0, 0, 0, 1, 3, 3, 3] avant : [1, 1, 1, 1, 1, 1, 1] après : [1, 1, 1, 1, 1, 1, 1] avant : [3, 3, 2, 2, 2, 1, 0] après : [0, 1, 2, 2, 2, 3, 3] avant : [1, 2, 2, 2, 2, 3, 3] après : [1, 2, 2, 2, 2, 3, 3]
aide Pythonitération conditionnelle (documentation Python)
while condition : blocWhile
nombres aléatoires (documentation Python)
import randommodule Python à importer pour manipuler des nombres aléatoires.
random.random()retourne un nombre réel aléatoirement compris entre
0inclus et1exclu.random.randint(min,max)retourne un nombre entier aléatoirement compris entre
minetmaxinclus.random.choice(s)retourne un élément de la séquence s (s non vide) choisi aléatoirement.
listes (documentation Python)
s[i] = xl'élément de rang
ide la listesest remplacé parx.del s[i]l'élément de rang
ide la listesest supprimé; la longueur de la liste diminue d'une unité.s.append(x)xest ajouté à la fin de la listes; la longueur de la liste augmente d'une unité.s.insert(i, x)xest inséré au rangidans la listes; la longueur de la liste augmente d'une unité.range(start=0, stop, step=1)génère la liste des entiers
startinclus (0 par défaut) àstopexclu par pas destep(1 par défaut).
Votre réponse :
AAV2_ITE: Méthode
Définir les 4 caractéristiques de la méthode de l'invariant dans le cas particulier de l'énoncé.
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie AAV5_ITE: Résultat
Utiliser l'interpréteur Python ci-dessous pour programmer l'algorithme demandé.
python : essai.pyOutputAAV3_ITE: Vérification
Appliquer cette technique au résultat proposé.
Si la technique proposée nécessite Python, on la mettra en œuvre dans l'interpréteur ci-dessus (cf. Résultats).
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie
Une solution possible :
AAV2_ITE: Choisir et appliquer une méthode générique
On utilise la méthode de l'invariant pour classer les cartes en précisant les 4 caractéristiques de la méthode : initialisation, invariant, condition d'arrêt, progression.
On s’intéresse à la carte courante de la main, dont on teste la couleur, et selon le résultat on procède à des échanges, de sorte qu'on ait à chaque étape à gauche une zone de piques, puis une zone de cœurs, puis une zone de carreaux, puis une zone inconnue et enfin, à droite une zone de trèfles.
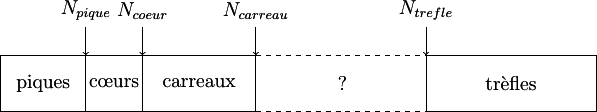
On peut utiliser une variable \(N_{pique}\), indice de la première carte après la zone « pique » connue; une variable \(N_{coeur}\), indice de la première carte après la zone « coeur » connue; une variable \(N_{carreau}\), indice de la première carte après la zone « carreau » connue; et une variable \(N_{trefle}\), indice de la première carte avant la zone « trèfle » connue.
Soient :
pique,coeur,carreau,trefle = 0,1,2,3les couleurs du jeu;couleurs = [pique,coeur,carreau,trefle]la liste des couleurs;main = [random.choice(couleurs),...,random.choice(couleurs)]la « main » à ordonner.Méthode de l'invariant Classer par couleurs initialisation npique,ncoeur,ncarreau,ntrefle = 0,0,0,len(main)-1
invariant à chaque étape, les cartes à gauche de l'indice ncarreausont classées par couleurs dans l'ordre pique, cœeur, carreau; les cartes à droite dentreflesont des trèfles.condition d'arrêt ncarreau > ntrefleprogression selon la couleur de main[ncarreau], échanger les cartes concernées et faire évoluer les indicesnpique,ncoeur,ncarreauetntrefleen conséquence.boucle npique,ncoeur,ncarreau,ntrefle = 0,0,0,len(main)-1 while ncarreau <= ntrefle : if main[ncarreau] == carreau : ncarreau = ncarreau + 1 elif main[ncarreau] == coeur : main[ncarreau], main[ncoeur] = main[ncoeur], main[ncarreau] ncoeur = ncoeur + 1 ncarreau = ncarreau + 1 elif main[ncarreau] == pique : main[ncarreau], main[npique] = main[npique], main[ncarreau] npique = npique + 1 if npique > ncoeur : ncoeur = ncoeur + 1 if ncoeur > ncarreau : ncarreau = ncarreau + 1 else : main[ncarreau], main[ntrefle] = main[ntrefle], main[ncarreau] ntrefle = ntrefle - 1
AAV5_ITE: Répondre explicitement à la question posée
Le code Python qui classe les cartes par couleurs est présenté ci-dessous.
python : iteration-jeux-3.pyOutputAAV3_ITE: Choisir et appliquer une technique de vérification
On utilise un jeu de tests pour vérifier le bon fonctionnement de cet algorithme de classement sur différents types de « main » : 1 seule couleur, plusieurs couleurs non classées, plusieurs couleurs déjà classées, plusieurs couleurs classées en ordre inverse...
Les 6 exemples proposés dans l'énoncé sont bien vérifiés.
-
Code de César
Le code de César est une méthode de cryptage très simple utilisée par Jules César dans ses correspondances secrètes.
Le texte crypté s'obtient en remplaçant chaque lettre du texte original par une lettre à distance fixe, toujours du même côté, dans l'ordre de l'alphabet. Dans un décalage à droite, on reprend au début de l'alphabet pour les dernières lettres de l'alphabet : ...x,y,z,a,b,c... Dans un décalage à gauche, on reprend à la fin de l'alphabet pour les premières lettres : ...c,b,a,z,y,x...
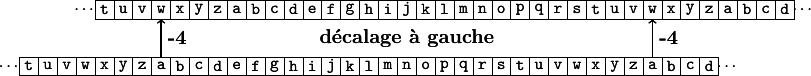
Ecrire un algorithme qui propose la traduction du texte original lorsqu'on connaît le décalage. On n'utilisera que les 26 lettres minuscules
abcdef...xyzde l'alphabet.Exemples :
texte original décalage traduction hal1 ibmkzbuoiorgzxgjaizout-6 etvoicilatraductionnzopopufwpdnpdlc-11 codedejulescesarljvsluhapvuhslkpunluplbyzkliylza19 ecolenationaledingenieursdebrestaide Pythonitération conditionnelle (documentation Python)
while condition : blocWhile
codage des caractères (documentation Python)
chr(n)retourne le caractère correspondant au code ASCII
n(\(n \in [0,255]\)).ord(c)retourne le code ASCII du caractère
c.
Votre réponse :
AAV2_ITE: Méthode
Définir les 4 caractéristiques de la méthode de l'invariant dans le cas particulier de l'énoncé.
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie AAV5_ITE: Résultat
Utiliser l'interpréteur Python ci-dessous pour programmer l'algorithme demandé.
python : essai.pyOutputAAV3_ITE: Vérification
Appliquer cette technique au résultat proposé.
Si la technique proposée nécessite Python, on la mettra en œuvre dans l'interpréteur ci-dessus (cf. Résultats).
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie
Une solution possible :
AAV2_ITE: Choisir et appliquer une méthode générique
On utilise la méthode de l'invariant pour décoder les caractères du texte crypté, en précisant les 4 caractéristiques de la méthode : initialisation, invariant, condition d'arrêt, progression.
Soient :
debut, fin = ord('a'), ord('z')les codes ASCII deaet dez;textele texte crypté;decalagele décalage utilisé pour crypter le texte.Méthode de l'invariant Code de César initialisation i, traduction = 0, ""
invariant à chaque étape i,traductionreprésente la chaîne desipremiers caractères décodés.condition d'arrêt i == len(texte)progression décoder le caractère courant cet ajouter le caractèrecodeobtenu à la fin de la chaînetraductionrecherchée.boucle i, traduction = 0, "" while i < len(texte) : c = texte[i] code = (ord(c)-debut + decalage)%(fin-debut+1) + debut traduction = traduction + chr(code) i = i + 1
AAV5_ITE: Répondre explicitement à la question posée
Le code Python qui décrypte un texte est présenté ci-dessous.
python : iteration-jeux-4.pyOutputAAV3_ITE: Choisir et appliquer une technique de vérification
On utilise un jeu de tests pour vérifier le bon fonctionnement de cet algorithme de cryptage : les 5 exemples proposés dans l'énoncé sont bien retrouvés.
-
Calcul de pi (somme)
Ecrire un algorithme qui calcule \(\pi\) à l'ordre \(n\) selon l'approximation :
\[\frac{\pi}{4} = 1 - \frac{1}{3} + \frac{1}{5} - \cdots + (-1)^n\frac{1}{2n+1} = \sum_{k=0}^n (-1)^k\frac{1}{2k+1}\]aide Pythonitération conditionnelle (documentation Python)
while condition : blocWhile
Votre réponse :
AAV2_ITE: Méthode
Définir les 4 caractéristiques de la méthode de l'invariant dans le cas particulier de l'énoncé.
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie AAV5_ITE: Résultat
Utiliser l'interpréteur Python ci-dessous pour programmer l'algorithme demandé.
python : essai.pyOutputAAV3_ITE: Vérification
Appliquer cette technique au résultat proposé.
Si la technique proposée nécessite Python, on la mettra en œuvre dans l'interpréteur ci-dessus (cf. Résultats).
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie
Une solution possible :
AAV2_ITE: Choisir et appliquer une méthode générique
On utilise la méthode de l'invariant pour calculer la somme \(\displaystyle\sum_{k=0}^n (-1)^k\frac{1}{2k+1}\), en précisant les 4 caractéristiques de la méthode : initialisation, invariant, condition d'arrêt, progression.
Méthode de l'invariant Calcul de pi initialisation k, signe, somme = 0, 1.0, 1.0
invariant à chaque étape k,sommereprésente la somme \(\displaystyle\sum_{i=0}^k (-1)^i\frac{1}{2i+1}\).condition d'arrêt k == nprogression ajouter à sommele terme suivant \(\displaystyle (-1)^k\frac{1}{2k+1}\).boucle k, signe, somme = 0, 1.0, 1.0 while k < n : k = k + 1 signe = - signe somme = somme + signe/(2*k + 1)
AAV5_ITE: Répondre explicitement à la question posée
Le code Python qui calcule \(\pi\) est présenté ci-dessous.
python : iteration-elem-1.pyOutputAAV3_ITE: Choisir et appliquer une technique de vérification
Une simple comparaison de valeurs avec la valeur bien connue de \(\pi\) (
math.pi: 3.141592653589793) suffit : le programme Python retrouve bien la valeur de \(\pi\).
-
Calcul de pi (produit)
Ecrire un algorithme qui calcule \(\pi\) à l'ordre \(n\) selon la formule :
\[\pi = 2\cdot \frac{4}{3}\cdot\frac{16}{15}\cdot\frac{36}{35}\cdot\frac{64}{63}\cdots = 2\prod_{k=1}^n\frac{4k^2}{4k^2 - 1}\]aide Pythonitération conditionnelle (documentation Python)
while condition : blocWhile
Votre réponse :
AAV2_ITE: Méthode
Définir les 4 caractéristiques de la méthode de l'invariant dans le cas particulier de l'énoncé.
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie AAV5_ITE: Résultat
Utiliser l'interpréteur Python ci-dessous pour programmer l'algorithme demandé.
python : essai.pyOutputAAV3_ITE: Vérification
Appliquer cette technique au résultat proposé.
Si la technique proposée nécessite Python, on la mettra en œuvre dans l'interpréteur ci-dessus (cf. Résultats).
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie
Une solution possible :
AAV2_ITE: Choisir et appliquer une méthode générique
On utilise la méthode de l'invariant pour calculer le produit \(\displaystyle\prod_{k=1}^n\frac{4k^2}{4k^2 - 1}\), en précisant les 4 caractéristiques de la méthode : initialisation, invariant, condition d'arrêt, progression.
Méthode de l'invariant Calcul de pi initialisation k, produit = 1, 4./3.
invariant à chaque étape k,produitreprésente le produit \(\displaystyle\prod_{i=1}^k\frac{4i^2}{4i^2 - 1}\).condition d'arrêt k == nprogression multiplier produitpar le terme \(\displaystyle\frac{4k^2}{4k^2 - 1}\).boucle k, produit = 1, 4./3. while k < n : k = k + 1 u = 4*k*k produit = produit*u/(u-1)
AAV5_ITE: Répondre explicitement à la question posée
Le code Python qui calcule \(\pi\) est présenté ci-dessous.
python : iteration-elem-2.pyOutputAAV3_ITE: Choisir et appliquer une technique de vérification
Une simple comparaison de valeurs avec la valeur bien connue de \(\pi\) (
math.pi: 3.141592653589793) suffit : le programme Python retrouve bien la valeur de \(\pi\).
-
Calcul de pi (rectangles)
On se propose de calculer \(\pi\) selon la méthode des rectangles.
Selon cette méthode, on calcule \(\pi\) à partir de l'expression de la surface \(S\) d'un cercle de rayon unité. On approche la surface du quart de cercle par \(n\) rectangles d'aire \(A_i = y_i/n\).
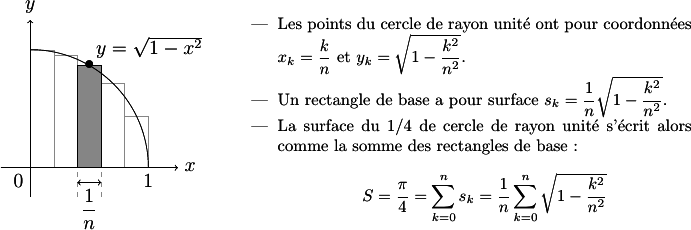
Ecrire un algorithme qui calcule \(\pi\) selon la méthode des rectangles à l'ordre \(n\).
aide Pythonitération conditionnelle (documentation Python)
while condition : blocWhile
Module math (documentation Python)
math.sqrt(x)retourne la racine carrée de
x: \(\sqrt{x}\).
Votre réponse :
AAV2_ITE: Méthode
Définir les 4 caractéristiques de la méthode de l'invariant dans le cas particulier de l'énoncé.
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie AAV5_ITE: Résultat
Utiliser l'interpréteur Python ci-dessous pour programmer l'algorithme demandé.
python : essai.pyOutputAAV3_ITE: Vérification
Appliquer cette technique au résultat proposé.
Si la technique proposée nécessite Python, on la mettra en œuvre dans l'interpréteur ci-dessus (cf. Résultats).
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie
Une solution possible :
AAV2_ITE: Choisir et appliquer une méthode générique
On utilise la méthode de l'invariant pour calculer la somme \(\displaystyle\sum_{k=0}^n \sqrt{1-\frac{k^2}{n^2}}\), en précisant les 4 caractéristiques de la méthode : initialisation, invariant, condition d'arrêt, progression.
Méthode de l'invariant Calcul de pi initialisation k, somme = 0, 1.0
invariant à chaque étape k,sommereprésente la somme \(\displaystyle\sum_{i=0}^k \sqrt{1-\frac{i^2}{n^2}}\).condition d'arrêt k == nprogression ajouter à pile terme \(\displaystyle\sqrt{1-\frac{k^2}{n^2}}\).boucle k, somme = 0, 1.0 while k < n : k = k + 1 somme = somme + math.sqrt(1 - (1.*k*k)/(n*n))
AAV5_ITE: Répondre explicitement à la question posée
Le code Python qui calcule \(\pi\) est présenté ci-dessous.
python : iteration-elem-3.pyOutputAAV3_ITE: Choisir et appliquer une technique de vérification
Une simple comparaison de valeurs avec la valeur bien connue de \(\pi\) (
math.pi: 3.141592653589793) suffit : le programme Python retrouve bien la valeur de \(\pi\).
-
Intégration numérique
Soit \(f(x)\) une fonction continue de \(R \rightarrow R\) à intégrer sur \([a,b]\). On supposera que \(f\) à toutes les bonnes propriétés mathématiques pour être intégrable sur l'intervalle considéré.
On cherche à calculer son intégrale \(\displaystyle I = \int_a^b f(x)dx\) qui représente classiquement l'aire comprise entre la courbe représentative de \(f\) et les droites d'équations \(x=a\), \(x=b\) et \(y=0\). Les principales méthodes d'intégration numérique consistent essentiellement à trouver une bonne approximation de cette aire.
Dans la méthode des rectangles, on subdivise l'intervalle d'intégration de longueur \(b-a\) en \(n\) parties égales de longueur \(\displaystyle\Delta x = \frac{b-a}{n}\).
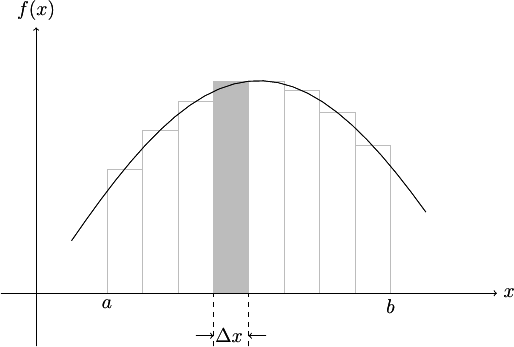
Soient \(x_1\), \(x_2\), ..., \(x_n\) les points milieux de ces \(n\) intervalles. Les \(n\) rectangles formés avec les ordonnées correspondantes ont pour surface \(f(x_1)\Delta x\), \(f(x_2)\Delta x\), ..., \(f(x_n)\Delta x\). L'aire sous la courbe est alors assimilée à la somme des aires de ces rectangles, soit :
\(\displaystyle I = \int_a^b f(x)dx \approx \left(f(x_1)+f(x_2)+\cdots+f(x_n)\right)\Delta x\)
C'est la formule dite des rectangles qui repose sur une approximation par une fonction en escalier.
Ecrire un algorithme qui calcule l'intégrale de \(\cos(x)\) sur \(\displaystyle \left[0,\frac{\pi}{2}\right]\) à l'ordre \(n\) par la méthode des rectangles.
aide Pythonitération conditionnelle (documentation Python)
while condition : blocWhile
Votre réponse :
AAV2_ITE: Méthode
Définir les 4 caractéristiques de la méthode de l'invariant dans le cas particulier de l'énoncé.
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie AAV5_ITE: Résultat
Utiliser l'interpréteur Python ci-dessous pour programmer l'algorithme demandé.
python : essai.pyOutputAAV3_ITE: Vérification
Appliquer cette technique au résultat proposé.
Si la technique proposée nécessite Python, on la mettra en œuvre dans l'interpréteur ci-dessus (cf. Résultats).
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie
Une solution possible :
AAV2_ITE: Choisir et appliquer une méthode générique
On utilise la méthode de l'invariant pour le calcul de la somme des rectangles, en précisant les 4 caractéristiques de la méthode : initialisation, invariant, condition d'arrêt, progression.
Soient :
f = math.cosla fonction à intégrer;a, b = 0., math.pi/2les bornes de l'intervalle d'intégration;nle nombre de rectangles;dx = (b - a)/nla largeur de chaque rectangle.Méthode de l'invariant Intégration numérique initialisation k, x = 1, a + dx/2 somme = f(x)*dx
invariant à chaque étape k, \(\displaystyle somme = \sum_{i = 0}^{k}f(x_i)\Delta x\)condition d'arrêt k == nprogression calculer l'aire du nouveau rectangle \(f(x)\Delta x\) et l'ajouter à la somme en cours. boucle k, x = 1, a + dx/2 somme = f(x)*dx while k < n : k = k + 1 x = x + dx aire = f(x) * dx somme = somme + aire
AAV5_ITE: Répondre explicitement à la question posée
Le code Python qui calcule l'intégrale est présenté ci-dessous.
python : iteration-prop-3.pyOutputAAV3_ITE: Choisir et appliquer une technique de vérification
On effectue le calcul analytique direct pour comparer avec la valeur obtenue par programme : on retrouve bien le résultat mathématique selon lequel \(\displaystyle\int_0^{\frac{\pi}{2}} \cos(x) dx = \left[\sin(x)\right]_0^{\frac{\pi}{2}} = \sin(\frac{\pi}{2}) - \sin(0) = 1 - 0 = 1\).
-
Zéro d'une fonction
On recherche le zéro d'une fonction \(f\) continue sur un intervalle \([a,b]\) telle que \(f(a).f(b) < 0\); il existe donc une racine de \(f\) dans \(]a,b[\) que l'on supposera unique.
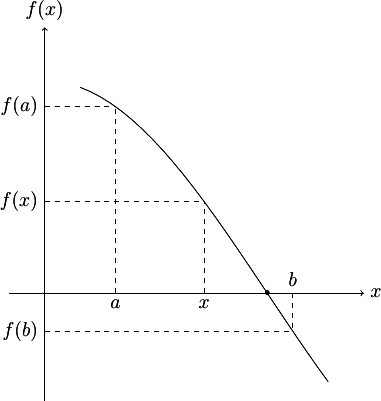
Les principales méthodes de recherche du zéro d'une fonction reposent sur une méthode par dichotomie. On sépare l'espace de recherche de la solution (ici l'intervalle \([a,b]\)) en 2 sous-espaces disjoints et, si on dispose d'un critère pour déterminer le sous-espace qui contient la solution recherchée (ici la condition \(f(a).f(b) < 0\)), on réitère la méthode sur le sous-espace candidat. A chaque étape, l'espace de recherche est ainsi divisé en 2 sous-espaces plus petits. Lorsque le sous-espace restant est considéré comme suffisamment petit, on estime avoir trouvé la solution (ici le zéro de la fonction).
Ici, notre critère de division de l'intervalle de recherche \([a,b]\) sera de le partager en deux par son milieu. Ainsi, on pose \(x_1 = a\), \(x_2 = b\) et \(x = (x_1+x_2)/2\) le milieu de \([x_1,x_2]\). Si \(f(x_1).f(x) < 0\), la racine est dans \(]x_1,x[\) et on pose \(x_2 = x\); sinon la racine est dans \(]x,x_2[\) et on pose \(x_1 = x\). Puis on réitère le procédé, la longueur de l'intervalle ayant été divisée par deux. Lorsque \(x_1\) et \(x_2\) seront suffisamment proches, on décidera que la racine est \(x\).
Ecrire un algorithme qui détermine le zéro de \(\cos(x)\) dans \([1,2]\) selon cette méthode par dichotomie.
aide Pythonitération conditionnelle (documentation Python)
while condition : blocWhile
Votre réponse :
AAV2_ITE: Méthode
Définir les 4 caractéristiques de la méthode de l'invariant dans le cas particulier de l'énoncé.
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie AAV5_ITE: Résultat
Utiliser l'interpréteur Python ci-dessous pour programmer l'algorithme demandé.
python : essai.pyOutputAAV3_ITE: Vérification
Appliquer cette technique au résultat proposé.
Si la technique proposée nécessite Python, on la mettra en œuvre dans l'interpréteur ci-dessus (cf. Résultats).
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie
Une solution possible :
AAV2_ITE: Choisir et appliquer une méthode générique
On utilise la méthode de l'invariant pour appliquer la méthode par dichotomie, en précisant les 4 caractéristiques de la méthode : initialisation, invariant, condition d'arrêt, progression.
Soient :
f = math.cosla fonction concernée;a, bles bornes de l'intervalle considéré;sle seuil d'arrêt des calculs;Méthode de l'invariant Zéro d'une fonction initialisation k, x1, x2 = 0, a, b x = (x1 + x2)/2
invariant à chaque étape k, \(x\) est le milieu de l'intervalle \([x_1,x_2]\).condition d'arrêt \(|x_2 - x_1| < s\) progression déterminer le sous-intervalle \([x_1,x]\) ou \([x,x_2]\) où se trouve le zéro puis calculer le nouveau milieu \(x\). boucle k, x1, x2 = 0, a, b x = (x1 + x2)/2 while math.fabs(x2 - x1) >= s : if f(x1)*f(x) < 0 : x2 = x else : x1 = x x = (x1 + x2)/2
AAV5_ITE: Répondre explicitement à la question posée
Le code Python qui calcule l'intégrale est présenté ci-dessous.
python : iteration-prop-4.pyOutputAAV3_ITE: Choisir et appliquer une technique de vérification
Une simple comparaison de valeurs avec la valeur facilement calculable du zéro de \(\cos(x)\) dans \([1,2]\) suffit : on retrouve bien que \(x = \pi/2 \approx 1.57\) est le zéro de \(\cos(x)\) dans l'intervalle \([1,2]\).