Définition de fonction

Réutiliser

Dans la pratique, on ne souhaite pas recopier 2 fois le même code d'autant plus si celui-ci nécessite de très nombreuses lignes de code. Pour améliorer la réutilisabilité de l'algorithme autrement que par un « copier-coller », une solution sera l'encapsulation du code à répéter au sein d'une « fonction » comme on en a l'habitude avec les fonctions mathématiques classiques : on « appelle » la fonction sinus (\(\sin(x)\)) plutôt que la redéfinir à chaque fois ! Ainsi, il arrivera souvent qu'une même séquence d'instructions doive être utilisée à plusieurs reprises dans un algorithme, et on souhaitera bien évidemment ne pas avoir à la reproduire systématiquement. Pour cela, le concepteur définira et utilisera ses propres « fonctions » qui viendront compléter le jeu d'instructions initial.

Structurer

L'approche efficace d'un problème complexe (comme coder un nombre fractionnaire) consiste souvent à le décomposer en plusieurs sous-problèmes plus simples (coder le signe, coder la mantisse, coder l'exposant) qui seront étudiés séparément. Ces sous-problèmes peuvent éventuellement être eux-mêmes décomposés à leur tour (coder la partie entière, coder la partie fractionnaire, normaliser), et ainsi de suite. Là encore, le concepteur définira et utilisera ses propres « fonctions » pour réaliser la structuration d'un problème en sous-problèmes : il divise le problème en sous-problèmes pour mieux le contrôler (diviser pour régner).

Encapsuler

>>> from math import sin, pi
>>> sin(pi/2)
1.0
>>> y = sin(pi/2)
>>> y
1.0

Cette petite session Python illustre quelques caractéristiques importantes des fonctions :

1. Une fonction à un nom : sin.

2. Une fonction est en général « rangée » dans une bibliothèque de fonctions (ici le module math de Python); il faut aller la chercher (on « importe » la fonction) : from math import sin.

3. Une fonction s'utilise (s'« appelle ») sous la forme d'un nom suivi de parenthèses; dans les parenthèses, on « transmet » à la fonction un ou plusieurs arguments : sin(pi/2).

4. L'évaluation de la fonction fournit une valeur de retour; on dit aussi que la fonction « renvoie » ou « retourne » une valeur (sin(pi/2) \(\rightarrow\) 1.0) qui peut ensuite être affectée à une variable : y = sin(pi/2).

5. Le code de la fonction n'est pas visible par l'utilisateur : on dit qu'il est « encapsulé » dans la fonction.

   

Une fonction en informatique se distingue principalement de la fonction mathématique par le fait qu'en plus de calculer un résultat à partir de paramètres, la fonction informatique peut avoir des « effets de bord » : par exemple afficher un message à l'écran, jouer un son, ou bien piloter une imprimante. Une fonction qui n'a pas d'effet de bord joue le rôle d'une expression évaluable. Une fonction qui n'a que des effets de bord est appelée une procédure et joue le rôle d'une instruction.

Les procédures et les fonctions intégrées au langage sont relativement peu nombreuses : ce sont seulement celles qui sont susceptibles d'être utilisées très fréquemment (voir par exemple les fonctions intégrées de Python). Les autres fonctions sont regroupées dans des fichiers séparés que l'on appelle « modules » en Python. Les modules sont donc des fichiers qui regroupent des ensembles de fonctions. Souvent on regroupe dans un même module des ensembles de fonctions apparentées que l'on appelle des bibliothèques. Pour pouvoir utiliser ces fonctions, il faut importer le module correspondant.

1. Built-in functions

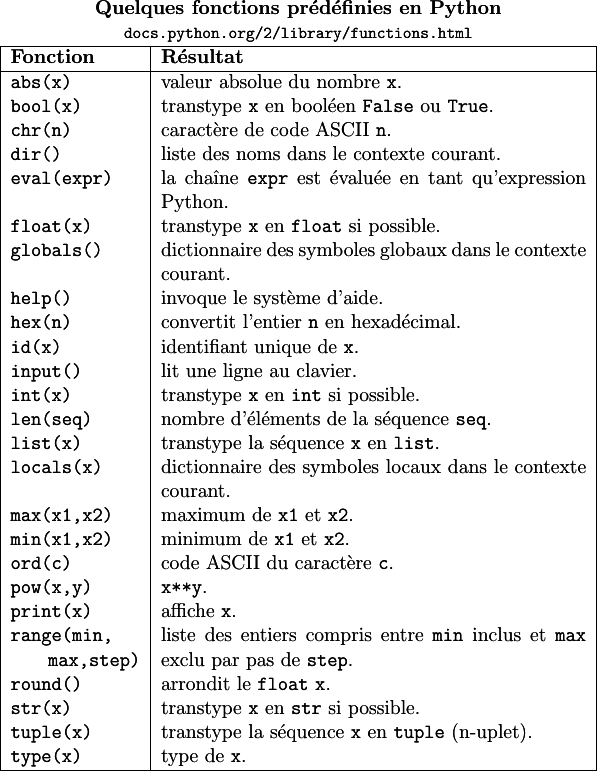
2. Mathematical functions

Ainsi en Python, il existe de nombreux modules additionnels dont le plus connu est le module math qui définit une vingtaine de constantes et fonctions mathématiques usuelles.

Sous l'interpréteur Python, on peut importer ce module de différentes manières :

1. La première méthode (from math import sin, pi) permet d'utiliser directement la fonction sin et la constante pi dans le programme (sin(pi/2)):

   >>> from math import sin, pi
   >>> sin(pi/2)
   1.0
   

   On peut également importer tous les « objets » d'un module (constantes, fonctions, classes) avec l'instruction:

   >>> from math import *
   >>> sin(pi/2)
   1.0
   >>> cos(pi)
   -1.0
   

   La simplicité de cette méthode a comme contrepartie que les « objets » importés pourraient entrer en conflit avec des « objets » de même nom déjà existants.

2. La deuxième méthode (import math) nécessite de rappeler le nom du module d'importation pour utiliser un « objet » du module (math.sin(math.pi/2)):

   >>> import math
   >>> math.sin(math.pi/2)
   1.0
   

   Il n'y a alors plus de conflit potentiel avec d'éventuels « objets » de même nom qui existeraient déjà.

Pour comprendre la différence entre ces deux méthodes, aidons-nous de la métaphore des cubes à la Lego. Nous disposons d'une boîte de cubes (lego) rangée sous la table.

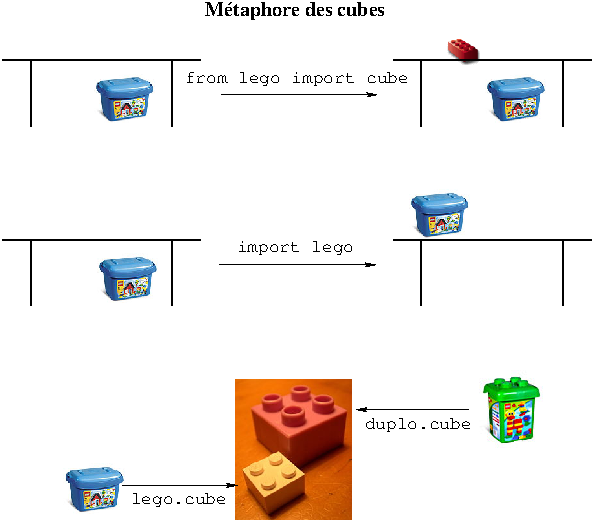
Pour utiliser un cube de cette boîte, nous pouvons soit prendre le cube dans la boîte et le mettre sur la table (from lego import cube) : le cube est alors directement accessible sur la table (cube); soit mettre la boîte sur la table (import lego) : le cube n'est alors pas directement accessible, il faut encore le prendre dans la boîte (lego.cube). L'intérêt de cette deuxième méthode est de distinguer 2 cubes qui porteraient le même nom (cube) mais qui ne seraient pas originaires de la même boîte (boîtes lego et duplo) et qui seraient donc différents (lego.cube et duplo.cube). Il est possible également de verser tout le contenu de la boîte sur la table (from lego import *) : ici, l'astérisque * signifie « tout »:

>>> from math import *
>>> sqrt(tan(log(pi)))
1.484345173593278

Méthode

Pour encapsuler un algorithme dans une fonction, on suivra pas à pas la démarche suivante :

1. donner un nom explicite à l'algorithme;
2. définir les paramètres d'entrée-sortie de l'algorithme;
3. préciser les préconditions sur les paramètres d'entrée;
4. décrire par une phrase ce que fait l'algorithme et dans quelles conditions il le fait;
5. donner des exemples d'utilisation et les résultats attendus;
6. encapsuler l'algorithme dans la fonction spécifiée par les 5 points précédents.

Les 5 premières étapes relèvent de la spécification de l'algorithme et la dernière étape concerne l'encapsulation proprement dite de l'algorithme. En Python, la spécification sera exécutable : à chaque étape, le code de la fonction est toujours exécutable même s'il ne donne pas encore le bon résultat; seule la dernière étape d'encapsulation permettra d'obtenir le résultat valide attendu.

Nommer

La première chose à faire est de nommer la fonction qui encapsule l'algorithme. Les noms de fonction sont des identificateurs arbitraires, de préférence assez courts mais aussi explicites que possible, de manière à exprimer clairement ce que la fonction est censée faire. Les noms des fonctions doivent en outre obéir à quelques règles simples :

1. Un nom de fonction est une séquence de lettres (a...z , A...Z) et de chiffres (0...9), qui doit toujours commencer par une lettre.
2. Seules les lettres ordinaires sont autorisées. Les lettres accentuées, les cédilles, les espaces, les caractères spéciaux tels que $,#,%... sont interdits, à l'exception du caractère _ (souligné).
3. La « casse » est significative : les caractères majuscules et minuscules sont distingués. Ainsi, sinus, Sinus, SINUS sont des fonctions différentes.
4. Par convention, on écrira l'essentiel des noms de fonction en caractères minuscules (y compris la première lettre). On n'utilisera les majuscules qu'à l'intérieur même du nom pour en augmenter éventuellement la lisibilité, comme dans triRapide ou triFusion.
5. Le langage lui-même peut se réserver quelques noms comme c'est le cas pour Python. Ces mots réservés ne peuvent donc pas être utilisés comme noms de fonction.

En ce qui concerne la fonction de Fibonacci, nous choisissons de l'appeler simplement fibonacci. Ce qui se traduira en Python par l'en-tête suivante où def et return sont deux mots réservés par Python pour définir les fonctions:

def fibonacci():
    return

Le code ci-dessus est la définition actuelle de la fonction fibonacci que l'on a éditée dans un fichier fibo.py. Dans l'état actuel, cette fonction n'a pas d'arguments et ne fait rien ! Mais elle est déjà compilable et exécutable.

On peut la décrire de la manière suivante : « La fonction fibonacci calcule un nombre de Fibonacci ».

Paramétrer

Un algorithme est une suite ordonnée d'instructions qui indique la démarche à suivre pour résoudre une série de problèmes équivalents. Dans ce contexte, c'est le paramétrage de l'algorithme qui lui donnera cette capacité recherchée de résoudre des problèmes équivalents. Dans l'exemple de la fonction sin, c'est en effet le paramètre x qui permet de calculer le sinus de n'importe quel nombre réel (sin(x)) et non le sinus d'un seul nombre.

La deuxième étape de la définition d'une fonction consiste donc à préciser les paramètres d'entrée-sortie de la fonction.

Pour cela, on nomme ces paramètres avec des identificateurs explicites dans le contexte courant d'utilisation de la fonction. Les paramètres de sortie seront systématiquement initialisés à une valeur par défaut; par exemple : 0 pour un entier, False pour un booléen, 0.0 pour un réel, '' pour une chaîne de caractères, [] pour une liste.

La fonction fibonacci prend l'ordre n en paramètre d'entrée et retourne le nombre u (\(u_n\)). Le paramètre de sortie u est un entier qui sera donc a priori initialisé à 0 dans la fonction et qui sera retourné par la fonction (return u):

def fibonacci(n):
    u = 0
    return u

Le code ci-dessus est la nouvelle définition de la fonction fibonacci toujours éditée dans le même fichier fibo.py que précédemment. Dans l'état actuel, cette fonction retourne 0 quels que soient le type et la valeur du paramètre d'entrée ! Mais elle est encore compilable et exécutable.

On peut maintenant la décrire de la manière suivante : « u = fibonacci(n) est le \(n^{i\grave eme}\) nombre de Fibonacci ». Cette description est un peu moins « littéraire » que la précédente. Elle a cependant l'avantage de montrer l'utilisation typique de la fonction (u = fibonacci(n)) et d'expliciter le sens des paramètres d'entrée-sortie (n et u).

Protéger

Dans la définition précédente de la fonction fibonacci, nous pouvons testé avec comme paramètre d'entrée la chaîne de caractères 'n' : cela n'a aucun sens pour le calcul d'un nombre de Fibonacci ! Il faut donc protéger la fonction pour la rendre plus robuste face à des contextes anormaux d'utilisation. Pour cela, on imposera aux paramètres d'entrée de vérifier certaines conditions avant d'exécuter la fonction appelée. Ces conditions préalables à l'exécution sont appelées les préconditions.

Une précondition est donc une expression booléenne qui prend soit la valeur False soit la valeur True. Elle peut contenir des opérateurs de comparaison (==, !=, >, >=, <=, <), des opérateurs logiques (not, and, or), des opérateurs d'identité (is, is not), des opérateurs d'appartenance (in, not in) ou toutes autres fonctions booléennes. En Python, on définira les préconditions que doivent vérifier les paramètres d'entrée de la fonction à l'aide de la directive assert. A l'exécution du code, cette directive « lèvera une exception » si la condition (l'assertion) testée est fausse. Les préconditions seront placées systématiquement juste après l'en-tête de la fonction (def fibonacci(n) :):

def fibonacci(n):
    assert type(n) is int
    assert n >= 0
    u = 0
    return u

La définition de la fonction fibonacci a donc été complétée par les préconditions sur le paramètre d'entrée : n doit être un entier (type(n) is int) positif ou nul (n >= 0). Sa description peut alors être complétée pour tenir compte de ces préconditions sur l'ordre n du nombre de Fibonacci calculé : « u = fibonacci(n) est le \(n^{i\grave eme}\) nombre de Fibonacci si n:int >= 0 ».

La fonction est toujours compilable et exécutable, mais son exécution est maintenant systématiquement interrompue si les préconditions ne sont pas respectées : ce qui est le cas pour les paramètres d'entrée -5 et 'n' par exemple. Dans tous les autres cas (entiers positifs ou nuls), elle retourne toujours 0 !

En Python, la manière dont nous avons initialisé le paramètre de sortie u (u = 0) indique qu'il s'agit implicitement d'un entier (int). La fonction fibonacci retourne donc un entier : c'est une postcondition sur le paramètre de sortie u dans le cas du calcul d'un nombre de Fibonacci.

En plus des préconditions et des postconditions, on pourra quelquefois imposer que des conditions soient vérifiées tout au long de l'exécution de la fonction : on parle alors d'invariants.

De tels exemples d'invariants seront mis en évidence lors de l'implémentation de certaines fonctions.

Décrire

Une fois choisis le nom de la fonction, les paramètres d'entrée-sortie et les préconditions sur les paramètres d'entrée, on peut alors préciser « ce que fait l'algorithme » et « dans quelles conditions il le fait » : il s'agit d'une phrase de description « en bon français » qui permettra à tout utilisateur de comprendre ce que fait l'algorithme sans nécessairement savoir comment il le fait.

Cette phrase est une chaîne de caractères qui doit expliciter le rôle des paramètres d'entrée et leurs préconditions, ainsi que toutes autres informations jugées nécessaires par le concepteur de la fonction. En particulier, lorsque le retour de la fonction n'est pas « évident », on explicitera les paramètres de sortie. Dans le cas de la fonction fibonacci, un utilisateur de la fonction « saura » ce qu'est un nombre de Fibonacci et la précision que cette fonction retourne un entier n'est pas nécessaire. Par contre, si la fonction retourne plus d'une valeur, il faut au moins préciser l'ordre dans lequel elle les retourne. Ainsi par exemple, pour la fonction divmod(a,b) de la bibliothèque standard Python qui calcule le quotient q et le reste r de la division entière \(a\div b\), il faut préciser qu'elle retourne un n-uplet (tuple) dans l'ordre (q,r). Dans certains cas, il faut également préciser que la fonction effectue les calculs dans telles ou telles unités : c'est par exemple le cas des fonctions trigonométriques usuelles où les calculs sont menés avec des angles en radians. Dans d'autres cas encore, on pourra préciser une référence bibliographique ou un site Web où l'utilisateur pourra trouver des compléments sur la fonction et l'algorithme associé.

La description d'une fonction intègrera donc au moins :

1. un exemple typique d'appel de la fonction,
2. la signification des paramètres d'entrée-sortie,
3. les préconditions sur les paramètres d'entrée.

En ce qui concerne la fonction fibonacci, nous l'avons fait évoluer au fur et à mesure en tenant compte de ces 3 recommandations : « u = fibonacci(n) est le \(n^{i\grave eme}\) nombre de Fibonacci si n:int >= 0 ».

1. exemple typique d'appel de la fonction : u = fibonacci(n),
2. signification des paramètres d'entrée-sortie : u est le \(n^{i\grave eme}\) nombre de Fibonacci,
3. préconditions sur les paramètres d'entrée : n:int >= 0

En Python, on intègrera cette description dans une docstring (chaîne entre 3 guillemets). Cette chaîne spéciale, qui peut tenir sur plusieurs lignes, joue le rôle de commentaire dans le corps de la fonction. Elle ne change donc rien à son exécution. Par contre, elle permettra de documenter automatiquement l'aide en-ligne de Python (help) ou encore, elle pourra être utilisée par certains environnements (idle par exemple) ou par certains utilitaires comme pydoc:

$ python
>>> import fibo4
6 0
>>> help(fibo4.fibonacci)
Help on function fibonacci in module fibo4:

fibonacci(n)
    u = fibonacci(n)
    nombre de Fibonacci à l'ordre n avec n:int >= 0.

La fonction est toujours compilable et exécutable; elle est maintenant documentable (help(fibo4.fibonacci)), mais retourne toujours 0 !

Jeu de tests

Avant même d'implémenter la fonction proprement dite, on définit des tests que devra vérifier la fonction une fois implémentée. Ces tests sont appelés tests unitaires car ils ne concernent qu'une seule fonction, la fonction que l'on cherche à définir.

Par exemple, on sait que fibonacci(0) devra retourner 1, fibonacci(1) devra retourner 1, fibonacci(2) devra retourner 2 ou encore fibonacci(9) devra retourner 55. En fait, quelle que soit la manière dont sera implémentée la fonction fibonacci, les résultats précédents devront être obtenus par cette implémentation.

Ainsi, on peut vérifier simplement si la fonction a passé le jeu de tests. C'est une manière de tester la validité de l'implémentation. Ces tests seront conservés tant que la fonctionnalité est requise. A chaque modification du code, on effectuera tous les tests ainsi définis pour vérifier si quelque chose ne fonctionne plus.

La plupart des langages proposent aujourd'hui des modules de tests. C'est le cas pour Python avec les modules doctest et unittest. Le module unittest est élaboré et l'est sans doute trop pour une initiation à l'algorithmique. Dans certains exercices de ce document, il sera néanmoins utilisé par l'auteur pour vérifier le code du lecteur, mais en toute transparence pour le lecteur. Quant au module doctest il n'est pas encore implémenté dans l'interpréteur en ligne utilisé dans ce document. Nous utiliserons donc une méthode indépendante de ces modules.

Nous définissons une variable tests qui est une liste de paires d'entrées-sorties. Par exemple pour fibonacci, nous retenons les 10 premiers nombres de Fibonacci:

tests = [(0,1), (1,1), (2,2), (3,3), (4,5), (5,8), (6,13), (7,21), (8,34), (9,55)]

Puis pour chaque paire d'entrées-sorties, nous comparons la valeur de la sortie avec ce que retourne la fonction testée (ici fibonacci) avec l'entrée associée:

for (entree,sortie) in tests :
    u = fibonacci(entree)
    verif = (sortie == u)
    print 'test :',entree,u,verif

En ce qui concerne la fonction fibonacci, elle est toujours compilable, exécutable et documentable; elle est maintenant testable, mais retourne toujours 0 et tous les tests échouent ! Il reste donc à l'implémenter.

Encapsuler

La dernière étape consiste enfin à dire « comment fait la fonction » pour répondre à la spécification décrite au cours des 5 étapes précédentes. En phase de spécification, la fonction (ou la procédure) est vue comme une boîte noire dont on ne connaît pas le fonctionnement interne.

En phase d'implémentation, l'enchaînement des instructions nécessaires à la résolution du problème considéré est détaillé.

Compte-tenu de la définition des nombres de Fibonacci, les instructions ci-dessous permettent de calculer le nombre u de Fibonacci pour un ordre n donné (n >= 2):

u1, u2 = 1, 1
k, u = 2, u1 + u2
while k < n :
    k = k + 1
    u2 = u1
    u1 = u
    u = u1 + u2

Pour chaque valeur de k, u1 représente initialement le nombre de Fibonacci à l'ordre (k-1), u2 le nombre de Fibonacci à l'ordre (k-2) et u = u1 + u2 le nombre de Fibonacci à l'ordre k.

Ce sont ces instructions qu'il faut encapsuler au cœur de la fonction fibonacci comme le montre le code complet ci-dessous.

Tester

Une fois implémentée, la fonction doit à minima se conformer au jeu de tests précédemment définis pour être « validée ». C'est le cas de la dernière version de la fonction fibonacci (fibo6.py).

C'est l'occasion de revenir sur le jeu de tests au regard de l'implémentation : couvre-t-on tous les cas typiques possibles ? La réponse à cette question est très souvent : non !

Sans entrer dans des techniques de génie logiciel pour mesurer la couverture de code, qui sortent du cadre de cette initiation à l'algorithmique, nous pouvons suivre quelques règles « simples » liées aux types de base et aux instructions de base que sont l'alternative et l'itération.

types de données:
	Tester les valeurs « nulles », elles sont assez souvent causes d'erreurs (comme la division par 0 par exemple) : type « zéro » int 0 float 0.0 str '' tuple () list [] dict {} Ces valeurs « nulles » sont considérées comme False lorque Python les interprète comme des booléens. Dans l'exemple de fibonacci qui concerne des entiers, le cas n = 0 est pris en compte dans le jeu de tests proposé.
alternative:	Prévoir autant de tests qu'il y a de branches dans l'alternative. Dans l'exemple de fibonacci, il y a une alternative simple: if n < 2 : # cas particuliers else : # cas général Il faut donc au moins un test pour n < 2 et un test pour n >= 2. Ce qui est fait dans le jeu de tests proposé.
itération:	Prévoir un test où on n'entre pas dans la boucle et un autre où on entre dans la boucle. Dans l'exemple de fibonacci, il y a une boucle while: k, u = 2, u1 + u2 while k < n : # corps de la boucle On testera donc le cas n = 2 qui ne passe pas dans la boucle puisque k = 2 à l'initialisation de la boucle qui a comme condition d'arrêt est k >= n. Ce qui est fait dans le jeu de tests proposé. On testera également un cas où k > 2 et k < n pour entrer dans la boucle. Ce qui est fait dans le jeu de tests proposé.

Bien entendu, il peut y avoir des itérations dans les branches d'une alternative et des alternatives dans les corps des itérations. Le nombre de tests peut donc ainsi croître de manière importante. Il est donc essentiel de définir des fonctions qui font peut de choses pour avoir un taux de couverture de code important et qui ne nécessitent que peu de tests pertinents pour être validables. De l'importance de structurer un algorithme en plusieurs fonctions : chaque fonction fait peu de choses mais le fait correctement et doit être validée par un jeu de tests pertinents.

Lorsque la fonction a été testée et validée, on ne souhaite naturellement plus exécuter le jeu de tests. On souhaite cependant le conserver dans le code pour le rejouer ultérieurement au cas où l'implémentation serait modifiée. En Python, on « protège » les tests par la condition:

if __name__ == "__main__" :
    # jeu de tests

qui contraint les jeux de tests à n'être évalués que lorsque le contexte d'exécution __name__ est le contexte principal ("__main__"). Ainsi la nouvelle version fonction_fibo7.py de la fonction fibonacci se présente de la manière suivante :

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43

# -*- coding: utf-8 -*- # Nommer la fonction, ici : fibonacci def fibonacci(n): # début description u""" u = fibonacci(n) nombre de Fibonacci à l'ordre n avec n:int >= 0. """ # fin description # début protection : mise en place des préconditions assert type(n) is int assert n >= 0 # fin protection # début initialisation u = 0 # fin initialisation # début implémentation if n < 2 : u = 1 else : u1, u2 = 1, 1 k, u = 2, u1 + u2 while k < n : k = k + 1 u2 = u1 u1 = u u = u1 + u2 # fin implémentation return u # début jeu de tests tests = [(0,1), (1,1), (2,2), (3,3), (4,5), (5,8), (6,13), (7,21), (8,34), (9,55)] for (entree,sortie) in tests : u = fibonacci(entree) verif = sortie == u print 'test fibonacci :',entree,u,verif # fin jeu de tests

Selon la manière de charger fonction_fibo7.py dans l'interpréteur Python standard, le contexte d'exécution sera global ou local à fonction_fibo7 :

• exécution dans le contexte principal "__main__":

  $ python fonction_fibo7.py
  test fibonacci : 0 1 True
  test fibonacci : 1 1 True
  test fibonacci : 2 2 True
  test fibonacci : 3 3 True
  test fibonacci : 4 5 True
  test fibonacci : 5 8 True
  test fibonacci : 6 13 True
  test fibonacci : 7 21 True
  test fibonacci : 8 34 True
  test fibonacci : 9 55 True
  $
  

  ou:

  $ python
  >>> execfile('fonction_fibo7.py')
  test fibonacci : 0 1 True
  test fibonacci : 1 1 True
  test fibonacci : 2 2 True
  test fibonacci : 3 3 True
  test fibonacci : 4 5 True
  test fibonacci : 5 8 True
  test fibonacci : 6 13 True
  test fibonacci : 7 21 True
  test fibonacci : 8 34 True
  test fibonacci : 9 55 True
  >>> globals()
  {'tests': [(0, 1), (1, 1), ..., (9, 55)],
  'entree': 9, 'sortie': 55, 'u': 55, 'verif': True,
  'fibonacci': <function fibonacci at 0xb74ca684>,
  ...
  '__name__': '__main__'}
  >>> fibonacci(9)
  55
  >>> exit()
  $
  

  Les tests et la fonction fibonacci sont dans le contexte principal : les tests sont exécutés. L'appel de la fonction est « direct » : fibonacci(9).

• exécution dans le contexte fonction_fibo7:

  $ python
  >>> import 'fonction_fibo7'
  >>> globals()
  {'fibo7': <module 'fonction_fibo7' from 'fonction_fibo7.pyc'>,
  ...
  '__name__': '__main__'}
  >>> fonction_fibo7.fibonacci(9)
  55
  >>> exit()
  $
  

  Les tests et la fonction fibonacci ne sont pas dans le contexte principal : les tests ne sont pas exécutés. Le nom de base du fichier joue le rôle d'un module fibo7 : l'appel de la fonction est « indirect » : fonction_fibo7.fibonacci(9).

Conclure

L'algorithmique, ou science des algorithmes, s'intéresse à l'art de construire des algorithmes ainsi qu'à caractériser leur validité, leur robustesse leur réutilisabilité, leur complexité ou encore leur efficacité. Certaines de ces caractéristiques générales (validité, robustesse, réutilisabilité) se concrètisent à la lumière des préconisations précédentes concernant la définition d'une fonction.

Validité:	La validité d'un algorithme est son aptitude à réaliser exactement la tâche pour laquelle il a été conçu. ie: L'implémentation de la fonction doit être conforme aux jeux de tests.
Robustesse:	La robustesse d'un algorithme est son aptitude à se protéger de conditions anormales d'utilisation. ie: La fonction doit vérifier impérativement ses préconditions.
Réutilisabilité:
	La réutilisabilité d'un algorithme est son aptitude à être réutilisé pour résoudre des tâches équivalentes à celle pour laquelle il a été conçu. ie: La fonction doit être correctement paramétrée.

Une fois la fonction définie (spécifiée et implémentée), il reste à l'utiliser (à l'appeler) : ce sera fait au chapitre suivant sur les appels de fonctions.