Fichier de rejeu Close
Indication Close
A propos de... Close
Commentaire Close
Téléchargements
Aide
Contexte EniBook
Présenter le contexte documentaire de cet EniBook sur l'algorithmique.
EniBook
Le projet
EniBook est un projet pédagogique initié en 2012 par Jacques TISSEAU à l'Ecole nationale d'ingénieurs de Brest (Enib). Ce projet concerne la conception et la réalisation d'un ensemble d'outils compatibles entre eux pour l'aide à la création de documents pédagogiques, numériques et interactifs sur la Toile.
- Du point de vue du lecteur, ces documents numériques se consultent et se manipulent uniquement à travers l'interface de leur navigateur Web (Chrome, Edge, Firefox, Internet Explorer, Opera, Safari...).
- Du point de vue de l'auteur, ces documents se rédigent dans un formalisme unique : le langage reStructuredText de l'environnement Sphinx/Python, sans avoir besoin de connaître ni le langage Python ni les langages du Web (Html, Css, Javascript...).
Un document créé dans le cadre de ce projet est appelé un... EniBook.
L'objet
Un EniBook est donc également :
- un document numérique interactif pour le Web ne nécessitant qu'un navigateur sur le poste de l'utilisateur : il est a priori indépendant de la plateforme sur laquelle il est consulté (stations, portables, tablettes, smartphones);
- un document à vocation pédagogique, du simple exercice interactif au manuel de cours interactif, accompagnant le lecteur dans ses apprentissages.
L'acronyme du projet a commencé avec celui des e-books (electronic book).
Un livre électronique n'étant pas nécessairement interactif, nous avons voulu insérer dans l'acronyme le « i » de interactive. On aurait ainsi pu obtenir le eibook (electronic interactive book). Mais nous avons préféré enibook (enib book) car en glissant le « n » entre le « e » et le « i », nous retrouvions l'acronyme de l'Enib. Ceci étant, un « livre Enib » ne dit rien sur sa nature numérique, d'où la volonté, tout en conservant l'acronyme enibook pour rappeler son origine, d'approfondir la définition de l'acronyme.
Le « n » de numerical traduit bien l'aspect numérique du document mais fait double emploi avec le « e » de electronic, d'où l'idée de supprimer ce « e » pour le remplacer par celui de embedded (embarqué) qui rappelle qu'un EniBook est « embarqué » dans le navigateur de l'utilisateur. Ainsi le « livre Enib » devient un « livre numérique embarqué et interactif » : embedded numerical interactive book.
Mais un EniBook n'est pas qu'un livre, c'est aussi un ensemble d'outils pour concevoir des EniBook : en quelque sorte un « kit » de conception. Ainsi le « k » de enibook participe à son tour à la définition de enibook ! Sachant par ailleurs qu'un EniBook est ouvert (open) à tous et disponible en ligne (online), chaque lettre de l'acronyme trouve naturellement sa place dans la définition :
EniBook : Embedded Numerical Interactive Book with Open Online Kit.
Cette version « descriptive » de l'acronyme dit ce qu'est un EniBook aujourd'hui. Mais elle ne nous apprend rien sur l'ambition d'un EniBook, à savoir celle de permettre au lecteur de se construire au fil du temps des connaissances par un couplage actif, au sens de l'énaction, avec le support numérique devenant lui-même de plus en plus pertinent. D'où cette version plus « visionnaire » de l'acronyme :
EniBook : Enactive Numerical Intelligent Book for Open Online Knowledge.
Par l'intermédiaire du menu principal d'un EniBook (icône en haut à droite de la fenêtre) :
- Le lecteur peut récupérer sous forme d'une archive
site.tar.gzl'ensemble des fichiers composant l'EniBook qu'il est en train de consulter. Une fois désarchivée sur son disque dur personnel, il lui suffit d'ouvrir le fichiersite/html/index.htmldans son navigateur pour pouvoir consulter cet EniBook en toutes circonstances, y compris hors connexion internet.- Les sources reStructuredText de l'EniBook en cours de consultation peuvent être téléchargées sous forme d'une archive
src.tar.gz. Une fois désarchivée, on peut recréer l'EniBook en (re)compilant le projet (make html). Le fichiersite/html/index.htmlest le point d'entrée de cette copie de l'EniBook original.- L'auteur peut récupérer sous forme d'une archive
enibook.tar.gzl'ensemble des fichiers permettant de créer un nouvel EniBook. Une fois désarchivée sur son disque dur personnel, il lui suffit de compléter le répertoireenibook/newproject(ou mieux, une copie de ce répertoire) avec ses propres fichiers reStructuredText, de compiler son projet (make html) pour créer le répertoiresite/spécifique à son projet d'EniBook. Le fichiersite/html/index.htmlest le point d'entrée de ce nouvel EniBook.
Outils interactifs
Présentation
Le projet EniBook repose aujourd'hui sur l'environnement Sphinx/Docutils/reStructuredText et reprend toutes les possibilités offertes par cet environnement de développement de documentation multi-format.
- Sphinx is a tool that makes it easy to create intelligent and beautiful documentation[...] Sphinx uses reStructuredText as its markup language, and many of its strengths come from the power and straightforwardness of reStructuredText and its parsing and translating suite, the Docutils.
- Docutils is an open-source text processing system for processing plaintext documentation into useful formats, such as HTML, LaTeX, man-pages, open-document or XML. It includes reStructuredText, the easy to read, easy to use, what-you-see-is-what-you-get plaintext markup language.
- reStructuredText is an easy-to-read, what-you-see-is-what-you-get plaintext markup syntax and parser system. It is useful for in-line program documentation (such as Python docstrings), for quickly creating simple web pages, and for standalone documents. reStructuredText is designed for extensibility for specific application domains.
Le projet EniBook utilise les outils de Docutils pour ajouter aux documents reStructuredText des extensions interactives. Cet EniBook en utilise plusieurs parmi lesquelles des QCM interactifs ou des interpréteurs Python en ligne.
Icones d'outils
En reStructuredText, les seuls outils interactifs sont les liens hypertextes internes ou externes (internet). Dans un EniBook, chaque outil interactif est repéré par un icone sur lequel on peut cliquer pour le déployer/rétracter afin de le manipuler.
Exemples d'outils
Les types d'outils les plus souvent utilisés dans cet EniBook sont les QCM et les interpréteurs Python.
QCM
Classiquement, un QCM est un test d'évaluation des connaissances. On distinguera la question à choix multiple du questionnaire à choix multiple :
- Une question à choix multiple est une question pour laquelle il est proposé plusieurs réponses possibles parmi lesquelles il faut choisir la (ou les) bonne(s) réponse(s).
- Un questionnaire à choix multiple est un ensemble de questions à choix multiple.
Deux cas se présentent alors pour les questions à choix multiple : les QCM à réponse unique et les QCM à réponses multiples. Dans les 2 cas, le bouton permet de tester sa réponse et le bouton permet de ré-initialiser le QCM en redistribuant aléatoirement les réponses.
Un QCM à réponse unique est composé d'une question, d'un certain nombre d'items possibles (5 dans l'exemple ci-dessous) parmi lesquels un et un seul item correspond à la réponse attendue.
QCM à réponse uniqueQuel est la couleur du cheval blanc d'Henri IV ?
- blanc
- noir
- isabelle
- bai
- alezan
Un QCM à réponses multiples est composé d'une question, d'un certain nombre d'items possibles (4 dans l'exemple ci-dessous) parmi lesquels 0 ou plusieurs items peuvent correspondre à la réponse attendue.
QCM à réponses multiplesSur la Terre, quand deux plaques lithosphériques se rapprochent,
- l'une peut plonger sous l'autre en créant une fosse océanique.
- un volcanisme de type explosif peut être la conséquence de ce mouvement.
- elles créent un risque sismique important.
- elles donnent naissance à une dorsale médio-océanique.
En mode apprentissage, des aides peuvent être proposées par le concepteur du QCM. Ces aides transforment alors le test classique en un véritable petit module d'apprentissage en lui-même. Ces aides peuvent faire le lien entre la question et le cours associé ou encore, mettre en avant des savoir-faire tels que des techniques de vérification par exemple. Deux cas se présentent alors :
L'aide est proposée dans la question pour orienter le choix vers la bonne réponse : on parle d'aide à priori ou de suggestion (hint).
QCM avec une aide dans la questionQuel est la couleur du cheval blanc d'Henri IV ?
HeuristiqueQuelquefois, la réponse est dans la question.
- blanc
- noir
- isabelle
- bai
- alezan
Une aide est apportée pour chaque item proposé : on parle d'aide à postériori ou de retour (feedback). En cas de mauvaise réponse, cette aide peut aider à trouver la bonne réponse. En cas de bonne réponse, il peut s'agir d'un complément d'information.
QCM avec des retours pour chaque itemQuel est la couleur du cheval blanc d'Henri IV ?
HeuristiqueQuelquefois, la réponse est dans la question.
- blanc
- noir
- isabelle
- bai
- alezan
- Vérification :
Le mot « blanc » est mentionné dans la question et il qualifie bien le cheval d'Henri IV : « cheval blanc d'Henri IV ».
- Remarque :
En France, ce sont les Haras nationaux qui définissent les « robes » des chevaux.
Voici un cheval blanc :
Et voici Henri IV sur son cheval blanc (Jean-Baptiste Mauzaisse, Portrait équestre d’Henri IV, huile sur toile, 1824, Musée national de Pau)... qui était gris selon Gotlib (Rubrique-à-brac)!
/01000/: - Vérification :
Le mot « noir » n'est pas dans la question.
- Remarque :
En France, ce sont les Haras nationaux qui définissent les « robes » des chevaux.
Voici un cheval noir :
/00100/: - Vérification :
Le mot « isabelle » n'est pas dans la question.
- Remarque :
En France, ce sont les Haras nationaux qui définissent les « robes » des chevaux.
Voici un cheval isabelle :
/00010/: - Vérification :
Le mot « bai » n'est pas dans la question.
- Remarque :
En France, ce sont les Haras nationaux qui définissent les « robes » des chevaux.
Voici un cheval bai :
/00001/: - Vérification :
Le mot « alezan » n'est pas dans la question.
- Remarque :
En France, ce sont les Haras nationaux qui définissent les « robes » des chevaux.
Voici un cheval alezan :
Un questionnaire à choix multiple regroupe plusieurs questions à choix multiple. Cliquer sur l'icone fait apparaître les différentes questions constituant le questionnaire.
2/2 QuestionnaireRappels
- Les questions sont indépendantes les unes des autres.
- A chaque ré-initialisation à l'aide du bouton , les questions sont présentées dans un ordre aléatoire et les items d'une même question sont redistribués aléatoirement.
- Après avoir validé chaque question à l'aide du bouton , le bilan « chiffré » du questionnaire peut être obtenu à l'aide du bouton .
Quel est la couleur du cheval blanc d'Henri IV ?
- blanc
- noir
- isabelle
- bai
- alezan
Sur la Terre, quand deux plaques lithosphériques se rapprochent,
- l'une peut plonger sous l'autre en créant une fosse océanique.
- un volcanisme de type explosif peut être la conséquence de ce mouvement.
- elles créent un risque sismique important.
- elles donnent naissance à une dorsale médio-océanique.
QCM Radio Checkbox Total Nombre de questions Réponses non enregistrées Réponses enregistrées Taux d'enregistrement Réponses enregistrées non validées Réponses enregistrées validées Taux de réussite partiel Taux de réussite total
Un EniBook particulier est consacré à la présentation des QCM.
Interpréteur Python
Cliquer sur l'icône pour ouvrir la fenêtre de l'interpréteur et de son éditeur associé.
Une fois l'interpréteur ouvert,
- l'icône renvoie à la documentation officielle de Python;
- l'icône donne accès à une fenêtre d'aide.
L'éditeur associé contient un programme Python qui trace
un polygone régulier de couleur c à n côtés de longueur d.
Le bloc
Commentaires
apporte quelques précisions sur ce code et on
peut lancer l'exécution du programme en cliquant sur le bouton
.
lignes 3-5: initialisation aléatoire du nombre n de côtés, de la longueur d d'un côté et de la couleur c du tracé lignes 9-11: initialisation de la tortue Logo t lignes 14-16: tracé du polygone régulier de couleur c à n côtés de longueur d
Un EniBook particulier est consacré à la présentation de l'interpréteur Python et de ses différents modules.
Utilisation
Structure du document
Cet EniBook est structuré en 3 grandes parties, chacune étant divisée elle-même en 3 chapitres :
- Contexte : présentation des contextes scientifique, pédagogique et documentaire qui ont permis d'élaborer ce document conçu par l'équipe pédagogique des enseignements d'informatique du premier semestre postbac de l'ENIB.
- Instructions de base : présentation des instructions d'affectation, d'alternative et d'itération, instructions de base de l'algorithmique.
- Fonctions : présentation des fonctions et procédures à travers leur définition, leurs appels simples et leurs appels récursifs.
Dans les parties « techniques », Instructions de base et Fonctions, chaque chapitre est composé de 2 ou 3 sections de cours et de 2 sections d'exercices (compréhension et programmation). Chaque section de cours propose des activités interactives et les exercices sont systématiquement corrigés selon la démarche MRV à l'exception des QCM.
Exercices de compréhension
Parmi les exercices de compréhension,
les QCM permettent essentiellement d'évaluer le degré de mémorisation des connaissances factuelles du cours;
Des exemples de questionnaires concernant les principales définitions rencontrées dans la section du Contexte informatique sont présentés ci-dessous (cliquer sur l'icône pour ouvrir la question correspondante).
les autres exercices testent la bonne compréhension des connaissances conceptuelles (cliquer sur l'icône pour ouvrir la question correspondante).
Des exemples de tels exercices sont présentés ci-dessous.
On cherche à faire dessiner une figure géométrique sur la plage à une personne qui a les yeux bandés. Quelle figure géométrique dessinera-t-elle en exécutant la séquence d'instructions ci-dessous ?
- avance de 20 pas;
- tourne à gauche de 90°;
- avance de 10 pas;
- tourne à gauche de 90°;
- avance de 20 pas;
- tourne à gauche de 90°;
- avance de 10 pas;
Rappels Python
tortue Logo (documentation Python)
import turtlemodule Python à importer pour manipuler la tortue Logo.
t = turtle.Turtle()crée une tortue
t.
t.down()tracer la trajectoire de la tortue Logo.
t.up()ne pas tracer la trajectoire de la tortue Logo.
t.setheading(a)oriente la tortue
tdans une direction qui fait l'anglea(en degrés) avec l'axe horizontal (sens trigonométrique).
t.forward(d)fait avancer la tortue
td'une distanceddans la direction courante.
t.backward(d)fait reculer la tortue
td'une distanceddans la direction courante.
t.left(a)fait tourner sur la gauche (sens trigonométrique) la tortue
t(sans avancer, ni reculer) d'un angleapar rapport à la direction courante.
t.right(a)fait tourner sur la droite (sens horaire) la tortue
t(sans avancer, ni reculer) d'un angleapar rapport à la direction courante.
t.goto(x,y)fait aller la tortue au point de coordonnées
(x,y)quelle que soit son orientation.Votre réponse :
AAV0_INT: Méthode
Appliquer cette méthode au cas particulier de l'énoncé.
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie AAV0_INT: Résultat
A la fin de la séquence d'instructions, la figure géométrique est un(e) ?
AAV0_INT: Vérification
Application de la technique
Si la technique proposée nécessite Python, on la mettra en œuvre dans l'interpréteur ci-dessus (cf. Résultat).
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie Une solution possible :
AAV0_INT: Choisir et appliquer une méthode générique
Pour dessiner la figure, on peut se mettre à la place de la personne (empathie) mais ne disposant pas nécessairement d'un espace suffisant pour exécuter l'algorithme, on le fera à l'échelle d'une feuille de papier en dessinant la figure (avec crayon, règle, compas, rapporteur) telle qu'elle est prescrite par l'énoncé. On parlera alors d'empathie géométrique pour effectuer ce « suivi de trajectoire ».
instruction trajectoire avance de 20 pas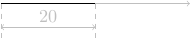 
tourne à gauche de 90°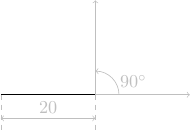 
avance de 10 pas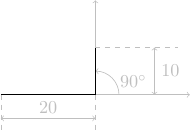 
tourne à gauche de 90°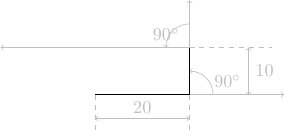 
avance de 20 pas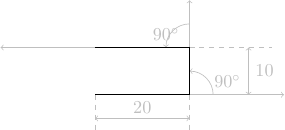 
tourne à gauche de 90°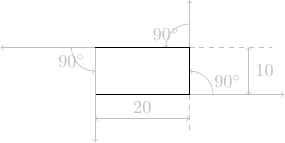 
avance de 10 pas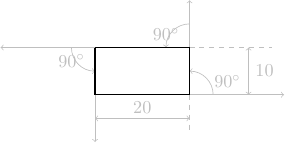 
AAV0_INT: Répondre explicitement à la question posée
La figure géométrique est un quadrilatère à 4 angles droits : c'est donc un rectangle.
AAV0_INT: Choisir et appliquer une technique de vérification
On peut traduire cette séquence d'instructions pour une tortue Logo et la faire exécuter par l'interpréteur Python.
En Python, on crée une tortue Logo par les instructions:
import turtle tortue = turtle.Turtle()On dit à la tortue Logo d'avancer de \(n\) pas par l'instruction:
tortue.forward(n*pas)où le pas représente finalement un facteur d'échelle (la longueur du pas est relative à la personne qui l'effectue).
On dit à la tortue Logo de tourner à gauche d'un angle \(a\) (en degrés) par l'instruction:
tortue.left(a)Le code ci-dessous propose la version Python de l'algorithme de l'énoncé.
python : essai.pyOutputLa figure obtenue par la tortue Logo est bien un rectangle, ce qui corrobore la réponse proposée.
On cherche à faire dessiner une figure géométrique sur la plage à une personne qui a les yeux bandés. Quelle figure géométrique dessinera-t-elle en exécutant la séquence d'instructions ci-dessous ?
- avance de 20 pas;
- tourne à gauche de 60°;
- avance de 20 pas;
- tourne à gauche de 120°;
- avance de 20 pas;
- tourne à gauche de 60°;
- avance de 20 pas;
Rappels Python
tortue Logo (documentation Python)
import turtlemodule Python à importer pour manipuler la tortue Logo.
t = turtle.Turtle()crée une tortue
t.
t.down()tracer la trajectoire de la tortue Logo.
t.up()ne pas tracer la trajectoire de la tortue Logo.
t.setheading(a)oriente la tortue
tdans une direction qui fait l'anglea(en degrés) avec l'axe horizontal (sens trigonométrique).
t.forward(d)fait avancer la tortue
td'une distanceddans la direction courante.
t.backward(d)fait reculer la tortue
td'une distanceddans la direction courante.
t.left(a)fait tourner sur la gauche (sens trigonométrique) la tortue
t(sans avancer, ni reculer) d'un angleapar rapport à la direction courante.
t.right(a)fait tourner sur la droite (sens horaire) la tortue
t(sans avancer, ni reculer) d'un angleapar rapport à la direction courante.
t.goto(x,y)fait aller la tortue au point de coordonnées
(x,y)quelle que soit son orientation.Votre réponse :
AAV0_INT: Méthode
Appliquer cette méthode au cas particulier de l'énoncé.
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie AAV0_INT: Résultat
A la fin de la séquence d'instructions, la figure géométrique est un(e) ?
AAV0_INT: Vérification
Application de la technique
Si la technique proposée nécessite Python, on la mettra en œuvre dans l'interpréteur ci-dessus (cf. Résultat).
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie Une solution possible :
AAV0_INT: Choisir et appliquer une méthode générique
Pour dessiner la figure, on peut se mettre à la place de la personne (empathie) mais ne disposant pas nécessairement d'un espace suffisant pour exécuter l'algorithme, on le fera à l'échelle d'une feuille de papier en dessinant la figure (avec crayon, règle, compas, rapporteur) telle qu'elle est prescrite par l'énoncé. On parlera alors d'empathie géométrique pour effectuer ce « suivi de trajectoire ».
instruction trajectoire avance de 20 pas 
tourne à gauche de 60°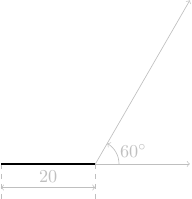 
avance de 20 pas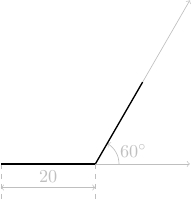 
tourne à gauche de 120°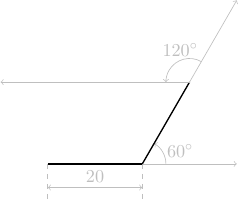 
avance de 20 pas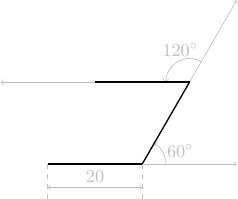 
tourne à gauche de 60°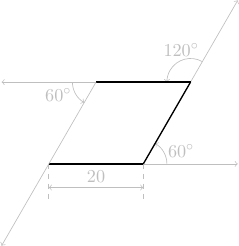 
avance de 20 pas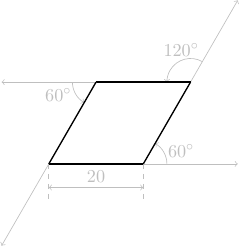 
AAV0_INT: Répondre explicitement à la question posée
La figure géométrique est un polygone à 4 côtés de même longueur : il s'agit donc d'un losange.
AAV0_INT: Choisir et appliquer une technique de vérification
On peut traduire cette séquence d'instructions pour une tortue Logo et la faire exécuter par l'interpréteur Python.
En Python, on crée une tortue Logo par les instructions:
import turtle tortue = turtle.Turtle()On dit à la tortue Logo d'avancer de \(n\) pas par l'instruction:
tortue.forward(n*pas)où le pas représente finalement un facteur d'échelle (la longueur du pas est relative à la personne qui l'effectue).
On dit à la tortue Logo de tourner à gauche d'un angle \(a\) (en degrés) par l'instruction:
tortue.left(a)L'interpréteur ci-dessous propose la version Python de l'algorithme de l'énoncé.
python : essai.pyOutputLa figure obtenue par la tortue Logo est bien un losange, ce qui corrobore la réponse proposée.
Remettre les 12 instructions ci-dessous dans le bon ordre pour obtenir un algorithme qui dessine une spirale rectangulaire à partir de son centre et en partant à l'horizontal.
Rappels
Spirale rectangulaires
Une spirale rectangulaire est une succession de segments de droite \(s_i\) telle que \(\forall i, \widehat{s_is_{i+1}} = \pi/2\mathrm{\ et\ } |s_{i+1}| = |s_i| + \Delta\).
Exemples de spirales rectangulaires :
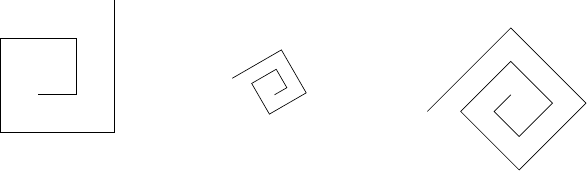
tortue Logo (documentation Python)
import turtlemodule Python à importer pour manipuler la tortue Logo.
t = turtle.Turtle()crée une tortue
t.
t.down()tracer la trajectoire de la tortue Logo.
t.up()ne pas tracer la trajectoire de la tortue Logo.
t.setheading(a)oriente la tortue
tdans une direction qui fait l'anglea(en degrés) avec l'axe horizontal (sens trigonométrique).
t.forward(d)fait avancer la tortue
td'une distanceddans la direction courante.
t.backward(d)fait reculer la tortue
td'une distanceddans la direction courante.
t.left(a)fait tourner sur la gauche (sens trigonométrique) la tortue
t(sans avancer, ni reculer) d'un angleapar rapport à la direction courante.
t.right(a)fait tourner sur la droite (sens horaire) la tortue
t(sans avancer, ni reculer) d'un angleapar rapport à la direction courante.
t.goto(x,y)fait aller la tortue au point de coordonnées
(x,y)quelle que soit son orientation.Votre réponse :
Résultat
1. Tracé d'une spirale rectangulaire
import turtletortue = turtle.Turtle()pas = 5tortue.forward(10*pas)tortue.left(90)tortue.forward(15*pas)tortue.left(90)tortue.forward(20*pas)tortue.left(90)tortue.forward(25*pas)tortue.left(90)tortue.forward(30*pas)
/0/: Commencer par créer la tortue.
/1/: Commencer par créer la tortue.
/2/: Définir le facteur d'échelle avant de l'utiliser.
/3/: Faire avancer la tortue de la plus petite longueur en partant à l'horizontal.
/.*/: Voici le type de spirale rectangulaire attendue :
Vérification
Nommer la technique utilisée pour vérifier le résultat obtenu :
?
Appliquer cette technique au résultat proposé.
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie Une solution possible :
Choisir et appliquer une méthode générique
On applique la méthode de l'empathie géométrique pour effectuer un « suivi de trajectoire ».
Répondre explicitement à la question posée
Le code Python ci-dessous effectue le suivi de trajectoire attendu.
python : essai.pyOutputChoisir et appliquer une technique de vérification
On exécute le code en Python pour vérifier qu'on obtient bien une spirale rectangulaire conforme par comparaison de figures aux figures données dans l'énoncé.
Remettre les 12 instructions ci-dessous dans le bon ordre pour obtenir un algorithme qui dessine l'étoile à 5 branches du drapeau européen en partant de la pointe en bas à gauche (sommet \(C\) sur la figure ci-dessous) et en montant directement vers la pointe en haut à droite (sommet \(E\) sur la figure ci-dessous).
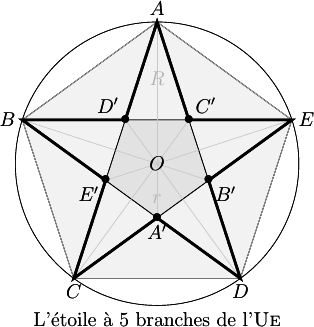Rappels Python
tortue Logo (documentation Python)
import turtlemodule Python à importer pour manipuler la tortue Logo.
t = turtle.Turtle()crée une tortue
t.
t.down()tracer la trajectoire de la tortue Logo.
t.up()ne pas tracer la trajectoire de la tortue Logo.
t.setheading(a)oriente la tortue
tdans une direction qui fait l'anglea(en degrés) avec l'axe horizontal (sens trigonométrique).
t.forward(d)fait avancer la tortue
td'une distanceddans la direction courante.
t.backward(d)fait reculer la tortue
td'une distanceddans la direction courante.
t.left(a)fait tourner sur la gauche (sens trigonométrique) la tortue
t(sans avancer, ni reculer) d'un angleapar rapport à la direction courante.
t.right(a)fait tourner sur la droite (sens horaire) la tortue
t(sans avancer, ni reculer) d'un angleapar rapport à la direction courante.
t.goto(x,y)fait aller la tortue au point de coordonnées
(x,y)quelle que soit son orientation.Votre réponse :
Résultat
1. Tracé d'une étoile à 5 branches
import turtletortue = turtle.Turtle()pas = 10tortue.left(36)tortue.forward(20*pas)tortue.left(144)tortue.forward(20*pas)tortue.left(144)tortue.forward(20*pas)tortue.left(144)tortue.forward(20*pas)tortue.left(144)tortue.forward(20*pas)
/0/: Commencer par créer la tortue. /1/: Commencer par créer la tortue. /2/: Définir le facteur d'échelle avant de l'utiliser. /3/: S'orienter dans la bonne direction. /.*/: Alterner orientation et avancement. Vérification
Nommer la technique utilisée pour vérifier le résultat obtenu :
?
Appliquer cette technique au résultat proposé.
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie Une solution possible :
Choisir et appliquer une méthode générique
On applique la méthode de l'empathie géométrique pour effectuer un « suivi de trajectoire ».
Répondre explicitement à la question posée
Le code Python ci-dessous effectue le suivi de trajectoire attendu.
python : essai.pyOutputChoisir et appliquer une technique de vérification
On exécute le code en Python pour vérifier qu'on obtient bien une étoile conforme par comparaison de figures à celle donnée dans l'énoncé.
Exercices de programmation
Les exercices de programmation sont classés selon leur domaine applicatif (types de données, jeux, tortue Logo...) et constituent autant d'opportunités pour appliquer les connaissances procédurales du cours.
Des exemples d'exercices de programmation sont présentés ci-dessous (cliquer sur l'icône pour ouvrir la question correspondante).
En s'inspirant des exemples précédents, écrire un programme qui dessine un segment de droite de 50 pas de long et qui fait un angle de \(\pi/6\) avec la verticale (par convention, les angles sont positifs dans le sens anti-horaire).
aide Pythontortue Logo : (documentation Python)
import turtlemodule Python à importer pour manipuler la tortue Logo.
t = turtle.Turtle()crée une tortue
t.
t.down()tracer la trajectoire de la tortue Logo.
t.up()ne pas tracer la trajectoire de la tortue Logo.
t.setheading(a)oriente la tortue
tdans une direction qui fait l'anglea(en degrés) avec l'axe horizontal (sens trigonométrique).
t.forward(d)fait avancer la tortue
td'une distanceddans la direction courante.
t.backward(d)fait reculer la tortue
td'une distanceddans la direction courante.
t.left(a)fait tourner sur la gauche (sens trigonométrique) la tortue
t(sans avancer, ni reculer) d'un angleapar rapport à la direction courante.
t.right(a)fait tourner sur la droite (sens horaire) la tortue
t(sans avancer, ni reculer) d'un angleapar rapport à la direction courante.
t.goto(x,y)fait aller la tortue au point de coordonnées
(x,y)quelle que soit son orientation.Votre réponse :
AAV0_INT: Méthode
Appliquer cette méthode au cas particulier de l'énoncé.
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie AAV0_INT: Résultat
Utiliser l'interpréteur Python ci-dessous pour programmer l'algorithme demandé.
python : essai.pyOutputAAV0_INT: Vérification
Application de la technique
Si la technique proposée nécessite Python, on la mettra en œuvre dans l'interpréteur ci-dessus (cf. Résultat).
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie Une solution possible :
AAV0_INT: Choisir et appliquer une méthode générique
On applique la méthode de l'empathie géométrique pour effectuer un « suivi de trajectoire ».
instruction trajectoire code Python s'orienter à 30° (\(\pi/6\)) de la verticale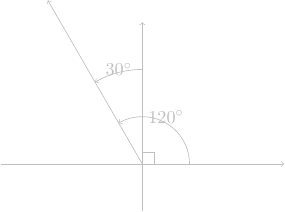 
tortue.left(90+30)avancer de 50 pas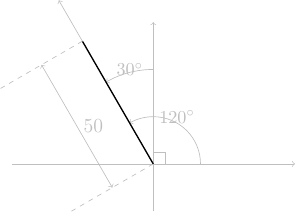 
tortue.forward(50*pas)AAV0_INT: Répondre explicitement à la question posée
Le code ci-dessous propose la version Python du tracé attendu.
python : essai.pyOutputAAV0_INT: Choisir et appliquer une technique de vérification
A ce stade, une simple comparaison de figures entre celle de l'énoncé et celle obtenue par programme suffira.
Les deux figures sont similaires, ce qui corrobore la réponse proposée.
En s'inspirant des exemples précédents, écrire un programme qui dessine un triangle \(ABC\) rectangle en \(A\) avec \(\theta_B = \widehat{ABC} = \pi/6\) et \(a = |BC| = 50\ \mathrm{pas}\).
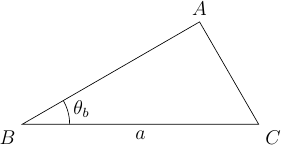aide Pythontortue Logo : (documentation Python)
import turtlemodule Python à importer pour manipuler la tortue Logo.
t = turtle.Turtle()crée une tortue
t.
t.down()tracer la trajectoire de la tortue Logo.
t.up()ne pas tracer la trajectoire de la tortue Logo.
t.setheading(a)oriente la tortue
tdans une direction qui fait l'anglea(en degrés) avec l'axe horizontal (sens trigonométrique).
t.forward(d)fait avancer la tortue
td'une distanceddans la direction courante.
t.backward(d)fait reculer la tortue
td'une distanceddans la direction courante.
t.left(a)fait tourner sur la gauche (sens trigonométrique) la tortue
t(sans avancer, ni reculer) d'un angleapar rapport à la direction courante.
t.right(a)fait tourner sur la droite (sens horaire) la tortue
t(sans avancer, ni reculer) d'un angleapar rapport à la direction courante.
t.goto(x,y)fait aller la tortue au point de coordonnées
(x,y)quelle que soit son orientation.Votre réponse :
AAV0_INT: Méthode
Appliquer cette méthode au cas particulier de l'énoncé.
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie AAV0_INT: Résultat
Utiliser l'interpréteur Python ci-dessous pour programmer l'algorithme demandé.
python : essai.pyOutputAAV0_INT: Vérification
Application de la technique
Si la technique proposée nécessite Python, on la mettra en œuvre dans l'interpréteur ci-dessus (cf. Résultat).
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie Une solution possible :
AAV0_INT: Choisir et appliquer une méthode générique
Dans le triangle \(ABC\) rectangle en \(A\), on a \(\theta_a = \pi/2\) et \(\theta_b = \pi/6\), d'où \(\theta_c = \pi - \pi/2 - \pi/6 = \pi/3\). On a également \(b = |AC| = a\sin(\pi/6)\) et \(c = |AB| = a\cos(\pi/6)\).
On applique la méthode de l'empathie géométrique pour effectuer un « suivi de trajectoire ».
instruction trajectoire code Python avancer de 50 pas 
tortue.forward(50*pas)tourner à gauche de 120°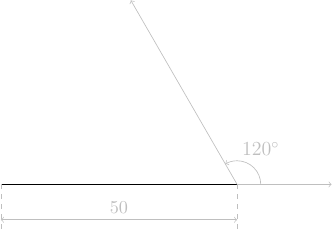 
tortue.left(120)avancer de 25 pas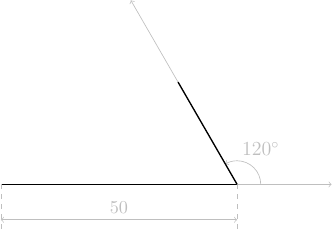 
tortue.forward(50*pas*(1./2))tourner à gauche de 90°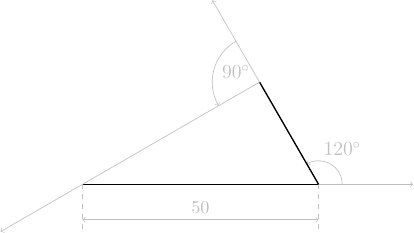 
tortue.left(90)avancer de \(\displaystyle 50\cdot\frac{\sqrt{3}}{2}\) pas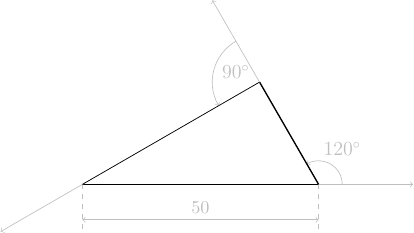 
tortue.forward(50*pas*(1.732/2))AAV0_INT: Répondre explicitement à la question posée
Le code ci-dessous propose la version Python du tracé attendu.
python : essai.pyOutputAAV0_INT: Choisir et appliquer une technique de vérification
A ce stade, une simple comparaison de figures entre celle de l'énoncé et celle obtenue par programme suffira.
Les deux figures sont similaires, ce qui corrobore la réponse proposée.
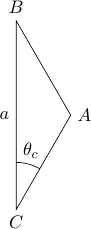
En s'inspirant des exemples précédents, écrire un programme qui dessine un triangle \(ABC\) isocèle en \(A\) tel que \(a = |BC| = 40\ \mathrm{pas}\) soit à la verticale et \(\theta_c = \widehat{ACB} = \pi/6\).
aide Pythontortue Logo : (documentation Python)
import turtlemodule Python à importer pour manipuler la tortue Logo.
t = turtle.Turtle()crée une tortue
t.
t.down()tracer la trajectoire de la tortue Logo.
t.up()ne pas tracer la trajectoire de la tortue Logo.
t.setheading(a)oriente la tortue
tdans une direction qui fait l'anglea(en degrés) avec l'axe horizontal (sens trigonométrique).
t.forward(d)fait avancer la tortue
td'une distanceddans la direction courante.
t.backward(d)fait reculer la tortue
td'une distanceddans la direction courante.
t.left(a)fait tourner sur la gauche (sens trigonométrique) la tortue
t(sans avancer, ni reculer) d'un angleapar rapport à la direction courante.
t.right(a)fait tourner sur la droite (sens horaire) la tortue
t(sans avancer, ni reculer) d'un angleapar rapport à la direction courante.
t.goto(x,y)fait aller la tortue au point de coordonnées
(x,y)quelle que soit son orientation.Votre réponse :
AAV0_INT: Méthode
Appliquer cette méthode au cas particulier de l'énoncé.
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie AAV0_INT: Résultat
Utiliser l'interpréteur Python ci-dessous pour programmer l'algorithme demandé.
python : essai.pyOutputAAV0_INT: Vérification
Application de la technique
Si la technique proposée nécessite Python, on la mettra en œuvre dans l'interpréteur ci-dessus (cf. Résultat).
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie Une solution possible :
AAV0_INT: Choisir et appliquer une méthode générique
Dans le triangle \(ABC\) isocèle en \(A\), on a \(\theta_b = \theta_c = \pi/6\) et \(\theta_a = 2\pi/3\). On a également \(a = |BC| = 40\ \mathrm{pas}\), d'où \(\displaystyle |AB| = |AC| = \frac{a}{2}\frac{1}{\cos(\theta_c)} = a\frac{1}{\sqrt{3}}\).
On applique la méthode de l'empathie géométrique pour effectuer un « suivi de trajectoire ».
instruction trajectoire code Python s'orienter à la verticale 
tortue.left(90)avancer de 40 pas 
tortue.forward(40*pas)tourner à droite de 150°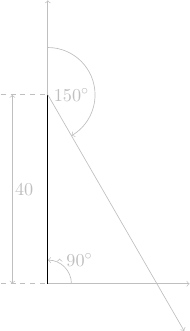 
tortue.right(150)avancer de \(\displaystyle 40\frac{1}{\sqrt{3}}\) pas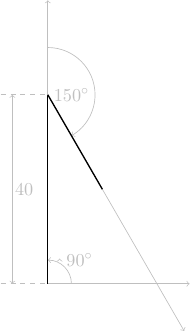 
tortue.forward(40*pas/1.732)tourner à droite de 60°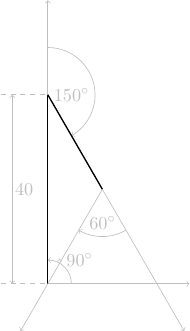 
tortue.right(60)avancer de \(\displaystyle 40\frac{1}{\sqrt{3}}\) pas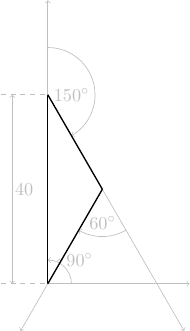 
tortue.forward(40*pas/1.732)AAV0_INT: Répondre explicitement à la question posée
Le code ci-dessous propose la version Python du tracé attendu.
python : essai.pyOutputAAV0_INT: Choisir et appliquer une technique de vérification
A ce stade, une simple comparaison de figures entre celle de l'énoncé et celle obtenue par programme suffira.
Les deux figures sont similaires, ce qui corrobore la réponse proposée.
Méthode de travail
Il ne s'agit pas ici d'imposer des méthodes de travail, mais de fournir des pistes pour ceux qui en cherchent.
- Dans tous les cas, l'expérience montre que :
- la seule présence, même attentive et active, aux séances de tutorat et de laboratoire ne suffit pas : il faut prévoir un temps de travail personnel qui, selon la personne et la matière, peut aller de 50% à 150% du temps de présence en classe;
- la régularité dans le travail personnel est un gage d'apprentissage plus efficace;
- pour savoir appliquer des connaissances procédurales, il faut pratiquer soi-même et ne pas se contenter de regarder les autres faire.
Dans un contexte de pédagogie inversée (flipped classrooms), « leçons à la maison (lectures at home) et devoirs en classe (homework in classes) », la pratique préalable de l'EniBook est évidemment essentielle pour des séances de tutorat et de laboratoire efficaces en terme d'apprentissage.
- Concernant les exercices,
- la solution est très souvent donnée ou connue; il faut donc savoir « jouer le jeu » pour ne pas simplement « recopier » la solution proposée (il existe d'ailleurs d'autres solutions pour la plupart des exercices) mais (re)trouver sa propre solution par une démarche personnelle;
- un apprenti programmeur est toujours confronté à ses propres erreurs; en général, ce sont des erreurs simples à corriger à condition de lire les messages d'erreur et de faire l'effort de les comprendre avant d'appeler « à l'aide »;
- lorsqu'on travaille sur un algorithme, il faut systématiquement se mettre mentalement à la place de la machine qui va l'exécuter (on parle alors d'« empathie numérique ») afin de vérifier le résultat obtenu; pour cela, il faut être méthodique et rigoureux; et petit à petit, à force de pratique, l'expérience fera qu'on « verra » le résultat produit par les instructions au fur et à mesure qu'on les écrit; naturellement, cet apprentissage est long, et demande des heures de travail patient; aussi, dans un premier temps, il faut éviter de sauter les étapes : la vérification méthodique, pas à pas, de chacun des algorithmes représente plus de la moitié du travail à accomplir.
- Concernant l'auto-apprentissage,
- Travailler un seul objectif à la fois.
- Pour un objectif donné, commencer par lire les sections de cours correspondantes puis, « dans la foulée » répondre à l'ensemble des QCM associés (section Exercices de compréhension - Connaître les définitions). En cas d'incertitude sur une réponse à un QCM, ne pas choisir au hasard une solution mais rechercher les éléments de réponse dans les sections de cours.
- Une fois que l'on répond aux QCM sans hésitation, passer aux autres exercices de compréhension pour tester la bonne compréhension des connaissances conceptuelles.
- Passer enfin aux exercices de programmation en s'attachant à y répondre en adoptant la démarche MRV. Cet EniBook en propose une vingtaine par objectif et s'il faut en privilégier certains pour des raisons de temps, choisir de préférence les exercices sur les types de données qui font partie des grands classiques de l'algorithmique ainsi que ceux sur la tortue Logo qui illustrent visuellement les principaux concepts d'algorithmique.
- Concernant les séances en présentiel,
- par respect pour les autres participants, la ponctualité aux séances en présentiel est de rigueur pour l'étudiant comme pour l'enseignant;
- pour plus d'efficacité, préparer les questions sur les problèmes en suspens avant la séance;
- en tutorat, l'ubiquité de l'enseignant n'étant pas possible, pratiquer le tutorat collaboratif où les 3 à 4 étudiants d'un groupe de travail s'entraident mutuellement;
- en laboratoire d'informatique, lorsqu'on travaille en binôme, il faut régulièrement alterner les rôles entre l'« écrivain » qui manipule clavier et souris et le « lecteur » qui vérifie la production de l'écrivain; à la fin du semestre, chaque étudiant doit être devenu un « lecteur-écrivain »; la pratique est en effet nécessaire pour « apprivoiser » l'environnement de travail afin que la machine devienne « transparente » et que seul subsiste le problème algorithmique à résoudre.