Fichier de rejeu Close
Indication Close
A propos de... Close
Commentaire Close
Algorithmique - Cours
- Objectif 1: affectation
- Objectif 2: alternative
- Objectif 3: itération
Téléchargements

Aide
Alternative
Présenter l'instruction conditionnelle et la mettre en œuvre dans le cadre du langage Python.
Les éléments de cours sont développés dans les 3 premières sections, les exercices associés dans la dernière section.
Définition
Extrait d'un dialogue entre un conducteur égaré et un piéton :
- Pourriez-vous m'indiquer le chemin de la gare, s'il vous plait ?
- Oui bien sûr : vous allez tout droit jusqu'au prochain carrefour. Si la rue à droite est autorisée à la circulation --- hier elle était en travaux --- alors prenez la et ensuite c'est la deuxième à gauche et vous verrez la gare. Sinon, au carrefour, vous allez tout droit et vous prenez la première à droite, puis encore la première à droite et vous y êtes.
- Merci.
Flux d'instructions
Sauf mention explicite, les instructions d'un algorithme sont exécutées les unes après les autres, dans l'ordre où elles ont été écrites dans le programme.
1 2 3 | instruction1
instruction2
instruction3
|
Le « chemin » suivi à travers un algorithme est appelé le flux d'instructions, et les constructions qui le modifient sont appelées des instructions de contrôle de flux. On exécute normalement les instructions de la première à la dernière, sauf lorsqu'on rencontre une instruction de contrôle de flux : de telles instructions vont permettre de suivre différents chemins suivant les circonstances. C'est en particulier le cas de l'instruction conditionnelle qui n'exécute une instruction que sous certaines conditions préalables.
Alternative simple
L'algorithme décrit par le piéton de l'exemple précédent propose une alternative
entre deux solutions.
Le conducteur égaré devra tester si la rue est en travaux avant de prendre
la décision d'aller à droite au carrefour ou de continuer tout droit.
En algorithmique, un tel choix est proposé par l'alternative simple,
instruction conditionnelle dite « if ... else » (si ... sinon):
if condition :
blocIf
else :
blocElse
L'instruction « if ... else » teste une condition.
Si la condition est vraie, alors le bloc d'instructions blocIf après le
« if condition : » (si condition) est exécuté.
Si la condition est fausse, c'est le bloc d'instructions blocElse après le
« else : » (sinon) qui est exécuté. Ainsi, seul l'un des 2 blocs est donc
exécuté.
L'alternative simple est une instruction de contrôle du flux d'instructions qui permet de choisir entre deux instructions selon qu'une condition est vérifiée ou non.
Une alternative simple se comporte comme un aiguillage de chemin de fer
dans le flux d'instructions.
Un « if ... else » ouvre deux voies correspondant à deux traitements
différents, et seule une de ces voies sera empruntée (un seul des deux
traitements est exécuté).
1 2 3 4 5 6 | instruction1
if condition :
blocIf
else :
blocElse
instruction3
|
Un grand classique
On veut affecter à la variable z le plus grand des deux nombres
x et y. Pour cela, il faut comparer les valeurs de ces 2 nombres
à l'aide d'un des opérateurs de comparaison : < (strictement inférieur),
<= (inférieur ou égal), >= (supérieur ou égal) ou >
(strictement supérieur). On choisit par exemple < : x < y.
Une telle expression vaut vrai si x est effectivement strictement
inférieur à y, faux sinon. Cette condition peut être testée dans une
alternative « if ... else » pour choisir le plus grand des deux:
if x < y :
z = y
else :
z = x
Pour une mise en œuvre effective en Python, x et y devront avoir été
préalablement initialisés.
Test simple
Dans certains langages comme Python, la partie else : est optionnelle;
on parle alors de test simple:
if condition :
blocIf
L'instruction « if » sous cette forme simplifiée
permet de tester la validité d'une condition.
Si la condition est vraie,
alors le bloc d'instructions blocIf après le « if condition : »
est exécuté. Si la condition est fausse, on passe à l'instruction
suivante dans le flux d'instructions.
1 2 3 4 | instruction1
if condition :
blocIf
instruction3
|
Le test simple est une instruction de contrôle du flux d'instructions qui permet d'exécuter une instruction sous condition préalable.
Le test simple est un cas particulier d'alternative simple où on explicite
le fait de ne rien faire (instruction pass en Python) dans le bloc
d'instructions associé au else:
if condition :
blocIf
else :
pass
Expressions booléennes
Opérateurs de comparaison
La condition évaluée après l'instruction « if » est donc une
expression booléenne qui prend soit la valeur False (faux) soit la valeur
True (vrai).
Elle peut contenir les opérateurs de comparaison suivants :
On veut utiliser une alternative simple pour calculer la valeur de l'expression \(xor = a \oplus b\) où \(a\) et \(b\) sont 2 variables booléennes et \(\oplus\) l'opérateur ou exclusif (xor).
Par définition, xor vaut True si a et b sont
différents, False sinon:
if a == b : xor = False
else : xor = True
Opérateurs booléens
Certains problèmes exigent parfois de formuler des conditions qui ne
peuvent pas être exprimées sous la forme d'une simple comparaison.
Par exemple, la condition \(x \in [0,1[\) s'exprime
par la combinaison de deux conditions \(x \geq 0\) et \(x < 1\) qui
doivent être vérifiées en même temps.
Pour combiner ces conditions, on utilise les opérateurs logiques
not (non : négation), and (et : conjounction) et or (ou : disjonction).
Ainsi la condition \(x \in [0,1[\) pourra s'écrire :
(x >= 0) and (x < 1).
Le tableau ci-dessous donne les tables de vérité des opérateurs not, or
et and, leur représentation graphique traditionnelle ainsi que leurs
principales propriétés.
A partir des 3 opérateurs de base, on peut définir des opérateurs dérivés tels que l'équivalence (\(\Leftrightarrow\)), l'implication (\(\Rightarrow\)) et la disjonction exclusive (\(\oplus\)).
0/0 Opérateurs dérivés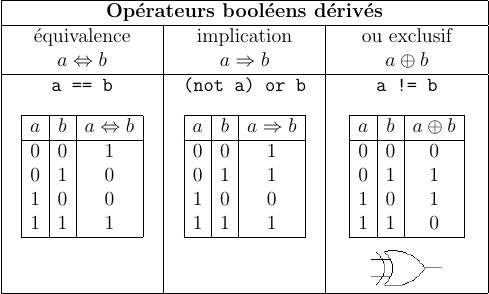
| QCM | Radio | Checkbox | Total |
|---|---|---|---|
| Nombre de questions | |||
| Réponses non enregistrées | |||
| Réponses enregistrées | |||
| Taux d'enregistrement | |||
| Réponses enregistrées non validées | |||
| Réponses enregistrées validées | |||
| Taux de réussite partiel | |||
| Taux de réussite total |
Entrées/SortiesPortes 1/1Portes 2/1Portes 3/1 |
| Vue d'ensemble | |
|---|---|
|
|
Empathie numérique
Méthode
Pour tenir compte des alternatives dans la méthode de l'empathie numérique, on insère une colonne « Conditions » avant celles des variables du problème.
Lorsqu'on rencontre une instruction d'alternative, on note la condition dans la
colonne des instructions
et on précise sa valeur (True ou False) dans la colonne « Conditions ».
Les lignes immédiatement suivantes du tableau correspondent aux instructions
du blocIf si la condition est vraie, à celles du blocElse si elle est
fausse.
| Exemple 1 | Exemple 2 |
x, y = 10, 5
if x < y :
z = y
else :
z = x
t = 2*z

|
x, y = 10, 50
if x < y :
z = y
else :
z = x
t = 2*z
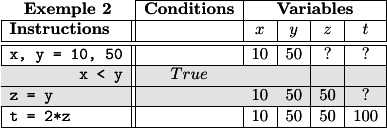
|
Vérification
Lorsque le code est une donnée de l'énoncé, comme c'est le cas dans les 2 exemples précédents, une technique de vérification « évidente » consiste à le faire exécuter directement par l'interpréteur Python.
Pour suivre pas à pas l'exécution de la séquence d'affectations tel que le préconise la méthode de l'empathie numérique, nous reprenons le code proposé et, après chaque instruction, nous affichons les valeurs des conditions et des variables qui interviennent dans ce code.
L'exécution par Python des séquences précédentes donne bien les mêmes résultats que ceux que nous avons obtenus « à la main ».
Alternatives en cascade
A pression ambiante, l'eau est sous forme de glace si la température est inférieure à \(0^\circ C\), sous forme de liquide si la température est comprise entre \(0^\circ C\) et \(100^\circ C\) et sous forme de vapeur au-delà de \(100^\circ C\).
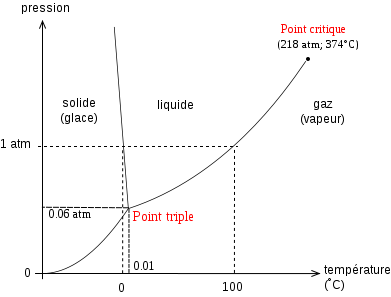
Cascade d'alternatives simples
Un algorithme qui devrait déterminer l'état de l'eau en fonction de la température doit pouvoir choisir entre trois réponses possibles : solide, liquide ou vapeur. Pour construire un tel algorithme, on cascade deux alternatives en testant la température de l'eau:
if temperature < 0 :
etat = 'glace'
else :
if temperature < 100 :
etat = 'liquide'
else :
etat = 'vapeur'
On commence par évaluer la première condition temperature < 0.
Si la condition est vérifiée, on exécute l'affectation etat = 'glace';
sinon (ie: temperature >= 0), on évalue la deuxième
condition temperature < 100 qui en fait est équivalente à
(temperature >= 0) and (temperature < 100).
Si la condition est vérifiée, on exécute l'affectation etat = 'liquide';
sinon (ie: temperature >= 100), on exécute l'affectation
etat = 'vapeur'.
La figure ci-dessous illustre le contrôle du flux d'instructions lors de deux
« if ... else » imbriqués : il s'agit de deux aiguillages en cascade.
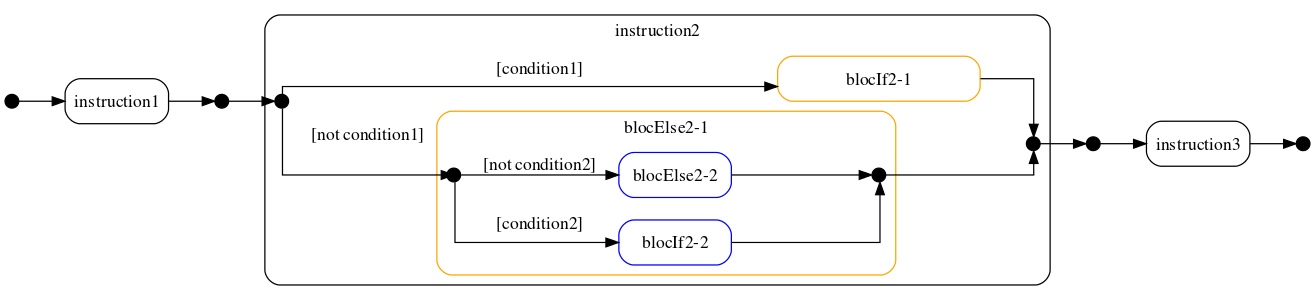
Alternative multiple
Dans certains langages comme Python, on peut
simplifier l'écriture des alternatives en cascade en contractant
le « else : if » en elif et obtenir une version plus compacte
strictement équivalente aux alternatives en cascade:
if temperature < 0 :
etat = 'glace'
elif temperature < 100 :
etat = 'liquide'
else :
etat = 'vapeur'
L'alternative multiple est une instruction de contrôle du flux d'instructions qui permet de choisir entre plusieurs instructions en cascadant des alternatives simples.
Méthode des discriminants
Quelle que soit la complexité d'une alternative (test simple, alternative simple ou alternative multiple), sa construction repose sur la détermination de conditions exclusives l'une de l'autre sur des variables discriminantes.
Pour construire une instruction d'alternative, on commencera donc par déterminer les variables discriminantes \((v_1,v_2,\ldots,v_n)\) du problème. Elles sont en général des données du problème ou des combinaisons de ces données.
Le problème est donc caractérisé par un n-uplet \((v_1,v_2,\ldots,v_n)\) à valeurs dans le domaine de définition \(E\), produit cartésien des domaines de définition \(E_i\) de chaque variable discriminante : \(E = E_1 \times E_2 \times \ldots \times E_n\).
Déterminer les conditions de l'alternative revient à effectuer une partition complète du domaine de définition \(E\) en \(r\) sous-ensembles \(S_k\) disjoints :
- Partition complète : \(\displaystyle E = S_1 \cup S_2 \cup \ldots \cup S_r = \bigcup_k S_k\)
- Sous-ensembles disjoints : \(\displaystyle\forall i,j:\ S_i \bigcap_{i\neq j} S_j = \{\}\)
Si la partition conduit à 2 sous-ensembles disjoints, une alternative simple suffit; si elle conduit à plus de 2 sous-ensembles disjoints, une alternative multiple est nécessaire. Si finalement, il n'y a pas de partition, le problème ne se traite pas par une alternative. La caractérisation de ces sous-ensembles est directement liée aux conditions de l'alternative.
Une fois définie la partition complète en sous-ensembles disjoints, la caractérisation des sous-ensembles permet de définir le squelette de l'alternative. Une fois ce squelette défini, il reste bien entendu à définir le traitement associé à chaque sous-ensemble.
Exemples d'alternatives simples
Le tableau ci-dessous montre l'application de la méthode des discriminants aux exemples de l'opérateur ou exclusif et du maximum de 2 nombres.
| Méthode des discriminants | Opérateur ou exclusif | Maximum de 2 nombres |
| variables discriminantes | les 2 booléens \(a\) et \(b\) | les 2 réels \(x\) et \(y\) |
| domaine de définition | le produit cartésien \(\mathbb{B}^2 = \{0,1\} \times \{0,1\}\) | le plan \(\mathbb{R}^2 = \mathbb{R} \times \mathbb{R}\) |
| nombres de sous-ensembles disjoints | 2 | 2 |
| définition des sous-ensembles | \(\{(a,b)\in\mathbb{B}^2| a = b \}\) et \(\{(a,b)\in\mathbb{B}^2| a \neq b \}\) | \(\{(x,y) \in \mathbb{R}^2|x < y\}\) et \(\{(x,y) \in \mathbb{R}^2|x \geq y\}\) |
| squelette de l'alternative | if a == b :
# sous-ensemble (a == b)
else :
# sous-ensemble (a != b)
|
if x < y :
# sous-ensemble (x < y)
else :
# sous-ensemble (x >= y)
|
Exemples d'alternatives multiples
Le tableau ci-dessous montre l'application de la méthode des discriminants à l'exemple des états de l'eau.
| Méthode des discriminants | Etats de l'eau |
| variables discriminantes | la température \(t\) de l'eau |
| domaine de définition | l'axe \(\mathbb{R}\) |
| nombres de sous-ensembles disjoints | 3 |
| définition des sous-ensembles | \(\{t\in\mathbb{R}| t < 0 \}\) et \(\{t\in\mathbb{R}| 0 \leq t < 100 \}\) et \(\{t\in\mathbb{R}| 100 \leq t \}\) |
| squelette de l'alternative | if t < 0 :
# sous-ensemble (t < 0)
elif t < 100 :
# sous-ensemble (t >= 0) and (t < 100)
else :
# sous-ensemble (t >= 100)
|



