Fichier de rejeu Close
Indication Close
A propos de... Close
Commentaire Close
Algorithmique - Cours
- Objectif 1: affectation
- Objectif 2: alternative
- Objectif 3: itération
Téléchargements

Aide
Affectation
Présenter l'instruction d'affectation et la mettre en œuvre dans le cadre du langage Python.
Les éléments de cours sont développés dans les 3 premières sections, les exercices associés dans la dernière section.
Liens utiles sur l'affectation :
Variable
Lors d'un premier séjour estival aux Etats-Unis, un étudiant français s'inquiéta de la température indiquée à la météo locale pour la journée à venir : \(70^\circ\)!
En fait, il s'agissait de degrés Fahrenheit (\(70^\circ F\)). Dans l'échelle de température de Fahrenheit, le point de solidification de l'eau est de 32 degrés (\(32^\circ F = 0^\circ C\)), et son point d'ébullition de 212 degrés (\(212^\circ F = 100^\circ C\)).
Mais combien font ces \(70^\circ F\) en degrés Celcius (\(^\circ C\)) plus habituels pour cet étudiant qui se demandait comment s'habiller par une telle température?
On souhaite ainsi convertir les degrés Fahrenheit (\(^\circ F\)) en degrés Celcius (\(^\circ C\)). Pour effectuer une telle conversion, nous commençons par donner un nom à la température Fahrenheit pour pouvoir en parler plus aisément, par exemple \(t_F\), ainsi qu'à la température Celcius, par exemple \(t_C\). Puis nous pouvons exprimer la relation générale qui lie \(t_C\) à \(t_F\) (voir le NIST guide to the SI par exemple) : \(\displaystyle t_C = \frac{5}{9}(t_F - 32)\).
Pour répondre à la question de l'étudiant, il reste à appliquer la relation précédente dans le cas particulier de l'étudiant : \(\displaystyle t_F = 70^\circ F \Rightarrow t_C = \frac{5}{9}(70 - 32) \approx 21^\circ C\).
Température de \(21^\circ C\) qui est évidemment plus conforme à ce que l'étudiant attendait.
Nommer pour abstraire
En informatique, l'essentiel du travail effectué par un programme d'ordinateur consiste à manipuler des données. Ces données peuvent être de type très divers (nombres, textes, images, sons, vidéos, jeux, programmes...) et pour accéder à ces données, il est pratique de les nommer plutôt que de connaître explicitement leur adresse en mémoire ou leur valeur. Nommer permet ainsi de s'abstraire des données spécifiques pour ne garder qu'une référence à ces données.
Une donnée apparaît ainsi sous un nom : on dit que le nom fait référence à une valeur (dénote une valeur). Pour la machine, il s'agit d'une référence désignant une adresse mémoire, c'est-à-dire un emplacement précis dans la mémoire vive où est stockée une valeur bien déterminée qui est la donnée proprement dite. En informatique, un nom est associé à un moment donné à une valeur d'un certain type et une seule.
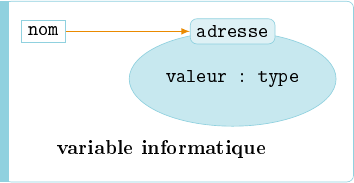
Une variable informatique est un quadruplet (nom, adresse, valeur, type) qui caractérise une donnée informatique à un instant donné.
Une variable peut ainsi être vue comme une case en mémoire vive, que le programme va repérer par une étiquette (une adresse ou un nom). Pour avoir accès au contenu de la case (la valeur de la variable), il suffit de la désigner par son étiquette : c'est-à-dire soit par son adresse en mémoire, soit par son nom. La taille de la case dépend du type de la donnée.
Les noms de variables sont des identificateurs arbitraires, de préférence assez courts tout en étant aussi explicites que possible, de manière à exprimer clairement ce que la variable est censée référencer (la sémantique de la donnée référencée par la variable).
Règles lexicales
Les noms des variables doivent en outre obéir à quelques règles lexicales simples :
Un nom de variable est une séquence de lettres (a ... z , A ... Z), de chiffres (0 ... 9) et du caractère
_(souligné), qui doit toujours commencer par une lettre ou par le caractère_.Exemples :
x,x1,x2,theta,tmp,mot,pression,longitude,_x,__name__Seules les lettres ordinaires sont autorisées. Les lettres accentuées, les cédilles, les espaces, les caractères spéciaux tels que
$,#,@, etc... sont interdits, à l'exception du caractère_(souligné).Exemples :
vitesse_angulaire,une_variable,une_autre_variableLa « casse » est significative : les caractères majuscules et minuscules sont distingués. Ainsi,
python,PythonetPYTHONsont des variables différentes.
Par convention, on écrira l'essentiel des noms de variable en caractères minuscules (y compris la première lettre). On n'utilisera les majuscules qu'à l'intérieur même du nom pour en augmenter éventuellement la lisibilité, comme dans
programmePythonouangleRotation. Une variable dont la valeur associée ne varie pas au cours du programme (on parle alors de constante) pourra être écrite entièrement en majuscule, par exemplePI(\(\pi = 3.14\)) ouROUGE(la couleur rouge).Le langage lui-même peut se réserver quelques noms comme c'est le cas pour Python (Table mots réservés en Python). Ces mots réservés ne peuvent donc pas être utilisés comme noms de variable.

| QCM | Radio | Checkbox | Total |
|---|---|---|---|
| Nombre de questions | |||
| Réponses non enregistrées | |||
| Réponses enregistrées | |||
| Taux d'enregistrement | |||
| Réponses enregistrées non validées | |||
| Réponses enregistrées validées | |||
| Taux de réussite partiel | |||
| Taux de réussite total |
Définition
Une fois nommée, il est souvent nécessaire de modifier la valeur de la donnée référencée par une variable. C'est le rôle de l'instruction d'affectation.
L'affectation est l'instruction qui associe une valeur à un nom de variable.

Associer nom et valeur d'une variable
L'instruction d'affectation est notée = en Python : nom = valeur.
Le nom de la variable à modifier est placé dans le membre de gauche du signe
=, la valeur qu'on veut lui attribuer dans le membre de droite.
Ainsi, les deux membres du signe = ne jouent pas le même rôle.
Le membre de droite de l'affectation est d'abord évalué sans être modifié.
Puis la valeur obtenue est affectée à la variable dont le nom est donné dans
le membre de gauche de l'affectation. Cette opération ne modifie
que le membre de gauche de l'affectation.
Evaluer le membre de droite
Le membre de droite d'une affectation peut être une constante ou une expression évaluable.
Cas d'une constante
La constante peut être d'un type quelconque : entier, réel, booléen, chaîne de caractères, tableau, matrice, dictionnaire... comme le suggèrent les exemples ci-dessous.
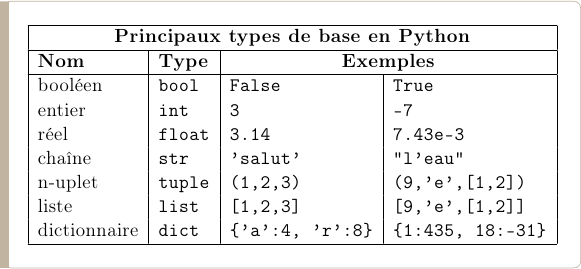
En Python, la valeur que l'on affecte à une variable impose dynamiquement
le type de la variable (Table Principaux types de base en Python). Ainsi,
si l'on affecte la valeur 3.14 à la variable x : x = 3.14,
celle-ci dénote alors un réel (type float en Python); si par contre,
on lui affecte la valeur 'salut': x = 'salut',
elle dénote alors une chaîne de caractères (type str en Python).
Cas d'une expression
L'expression peut être n'importe quelle
expression évaluable telle qu'une opération logique :
True or False and not True,
une opération arithmétique : 3 + 2*9 - 6*7,
un appel de fonction : sin(x) ou
toute autre combinaison évaluable :
(x != y) and (z + t >= y) or (sin(x) < 0).
L'expression du membre de droite peut faire intervenir la variable
du membre de gauche comme dans i = i+1. Dans cet exemple, on évalue
d'abord le membre de droite i+1 puis on attribue la valeur obtenue au
membre de gauche i; ainsi, à la fin de cette affectation,
la valeur de i a été augmentée de 1 :
on dit que i a été incrémenté de 1 et on parle
d'incrémentation
de la variable i.
Le langage Python propose un opérateur d'incrémentation +=
et d'autres opérateurs d'affectation
qui peuvent toujours se ramener
à l'utilisation de l'opérateur =, l'opérateur d'affectation de base.
Une instruction pas si simple que ça
L'affectation a donc pour effet de réaliser plusieurs opérations en mémoire :
0/0 Expression versus instruction
- créer et mémoriser une valeur particulière,
- créer et mémoriser un nom de variable,
- établir un lien (par un système interne de pointeurs) entre le nom de la variable et l'emplacement mémoire de la valeur correspondante,
- attribuer un type déterminé à la variable.
| QCM | Radio | Checkbox | Total |
|---|---|---|---|
| Nombre de questions | |||
| Réponses non enregistrées | |||
| Réponses enregistrées | |||
| Taux d'enregistrement | |||
| Réponses enregistrées non validées | |||
| Réponses enregistrées validées | |||
| Taux de réussite partiel | |||
| Taux de réussite total |
Séquences d'affectations
Une bonne manière de s'assurer que l'on a compris une notion algorithmique est de savoir lire un algorithme qui met en œuvre cette notion : lire un algorithme, c'est l'exécuter dans sa tête. On parle alors d'« empathie numérique » au sens où cela nécessite de « se mettre à la place de » l'ordinateur pour exécuter pas à pas les instructions qui composent l'algorithme.
Empathie numérique
Exemples
Lire pour programmerDéterminer « à la main » les valeurs des variables
a,b,qetraprès la séquence d'affectations suivante :a = 19 b = 6 q = 0 r = a r = r - b q = q + 1 r = r - b q = q + 1 r = r - b q = q + 1
A la fin de l'algorithme, l'instruction
print a,b,q,raffiche ?Déterminer « à la main » les valeurs des variables
a,betraprès la séquence d'affectations suivante :a = 12 b = 18 r = a%b a = b b = r r = a%b a = b b = r r = a%b a = b b = r
A la fin de l'algorithme, l'instruction
print a,b,raffiche ?
Indication
Textes à trous
| Bouton | Action |
|---|---|
| Initialiser toutes les zones de saisie | |
| Afficher cette aide | |
| Afficher le bilan de l'exercice |
| Clavier | Action |
|---|---|
| Enter | Valider la zone de saisie |
| F1 | Afficher une aide technique |
| F2 | Afficher une aide pédagogique |
| Ctrl-A | Tout sélectionner |
| Ctrl-C | Copier la sélection dans le presse-papier |
| Ctrl-V | Copier le presse-papier dans la sélection |
| Ctrl-X | Couper la sélection et la copier dans le presse-papier |
| Ctrl-Z | Annuler la modification |
| Maj-Ctrl-Z | Rétablir la modification |
| Question | Bilan |
|---|---|
| Nombre de trous | |
| Réponses non validées | |
| Réponses validées | |
| Taux de validation | |
| Réponses validées non attendues | |
| Réponses validées attendues | |
| Taux de réussite partiel | |
| Taux de réussite total |
Méthode
Pour déterminer les valeurs de variables après une séquence d'instructions, il faut suivre instruction après instruction (pas à pas) l'évolution des valeurs des variables concernées.
Il s'agit donc de suivre l'évolution des valeurs de \(r\) variables \(v_1, v_2, \ldots, v_r\) qui interviennent dans une séquence de \(n\) instructions \(i_1, i_2, \ldots, i_n\).
Pour suivre pas à pas (instruction par instruction) l'évolution des variables, on dresse un tableau où chaque ligne \(k\) correspond à une instruction \(i_k\) et chaque colonne \(j\) à une variable \(v_j\). Pour chaque instruction \(i_k\), on indique la valeur \(x_{k,j}\) que prend chaque variable \(v_j\) après exécution de l'instruction \(i_k\).
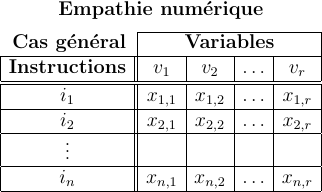
Si une variable n'a pas encore été initialisée au moment où on exécute
une instruction, on lui donne pour valeur le ? indiquant ainsi
qu'on ne connaît pas encore sa valeur.
On trouve dans la dernière ligne \(n\) du tableau, les valeurs
finales \(x_{n,1}, x_{n,2}, \ldots, x_{n,r}\) des \(r\) variables
\(v_1, v_2, \ldots, v_r\).
Ainsi, cette méthode de l'empathie numérique donne les résultats suivants pour les deux exemples précédents :
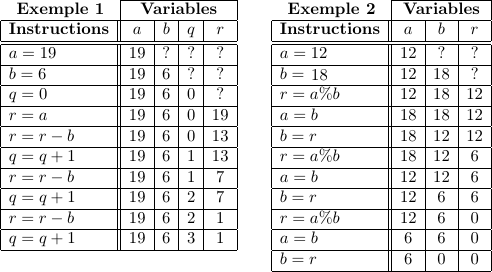
Vérification
Lorsque le code est une donnée de l'énoncé, comme c'est le cas dans les 2 exercices précédents, une technique de vérification « évidente » consiste à le faire exécuter directement par l'interpréteur Python.
Pour suivre pas à pas l'exécution de la séquence d'affectations tel que le préconise la méthode de l'empathie numérique, nous reprenons le code proposé et, après chaque instruction, nous affichons les valeurs des variables qui interviennent dans ce code.
L'exécution par Python des séquences précédentes donne bien les mêmes résultats que ceux que nous avons obtenus « à la main ».
Un grand classique
Version 1
Un apprenti informaticien à qui on demandait d'échanger (swap) les valeurs
de 2 variables x et y proposa la suite d'instructions suivante:
x = 10
y = 20
x = y
y = x
Il eut la désagréable surprise de constater que les valeurs des variables
n'étaient pas permutées après cette séquence d'affectations.
En effet, les variables sont respectivement initialisées par les
instructions x = 10 et y = 20.
L'affectation x = y conduit à évaluer y puis à attribuer la valeur
de y (20) à x : x vaut maintenant 20.
La deuxième affectation y = x commence par évaluer x puis à attribuer
la valeur de x (20) à y : y vaut maintenant 20.
Après ces 2 affectations, les valeurs de x et y sont donc identiques
(et égales à 20) et non permutées!
python : affectation-swap-1.py
Le problème de cette version vient du fait que la valeur initiale (10) de x
n'est plus référencée et donc... qu'on ne peut plus y faire référence.
Version 2
Pour effectuer la permutation, l'apprenti informaticien aurait pu utiliser
une variable temporaire tmp pour référencer la valeur initiale de x
et exécuter la séquence d'instructions suivante:
x = 10
y = 20
tmp = x
x = y
y = tmp
La première affectation (tmp = x) permet de stocker la valeur initiale
de x (10), la deuxième (x = y) attribue à x la valeur de y (20)
et la troisième (y = tmp) attribue à y la valeur de tmp,
c'est-à-dire la valeur initiale de x (10).
Ainsi, les valeurs finales de x et y (20 et 10) sont bien permutées
par rapport aux valeurs initiales (10 et 20).
python : affectation-swap-2.py
Version 3
En Python, les n-uplets permettent d'écrire plus simplement la permutation
de deux variables : x, y = y, x:
x = 10
y = 20
x, y = y, x
On commence par évaluer le membre de droite, soit la paire y,x qui vaut 20,10;
puis on attribue cette valeur au membre de gauche, soit à la paire x,y qui
vaut donc après affectation 20,10. Ainsi, le premier élément x de la paire
x,y vaut maintenant 20 et le second argument y vaut 10.
Les valeurs de x et de y ont dont bien été échangées par l'affectation
x, y = y, x.
python : affectation-swap-3.py
Généralisation
On peut utiliser la même technique (version 2 ou version 3) pour échanger des valeurs entre plus de 2 variables comme l'illustrent les 2 exercices suivants.
2 Décalages1. Permutation à 3 variables
3 variables
1. Décalage à droite
Remettre les 5 instructions suivantes dans le bon ordre
pour obtenir un algorithme qui opère un décalage à droite
des valeurs des 3 variables u, v, w.
- Avant permutation à droite :
u, v, w = 1, 2, 3- Après permutation à droite :
u, v, w = 3, 1, 2
u, v, w = 1, 2, 3tmp = ww = vv = uu = tmp
| /0/: | On commence par initialiser les variables. |
|---|---|
| /1/: | Après l'initialisation des variables, on sauvegarde une des valeurs initiales dans une variable temporaire. |
En utilisant les n-uplets de Python, on aurait pu écrire plus directement:
u, v, w = 1, 2, 3
u, v, w = w, u, v
2. Permutation à 5 variables
5 variables
1. Décalage à gauche
Remettre les 7 instructions suivantes dans le bon ordre
pour obtenir un algorithme qui opère un décalage à gauche
des valeurs des 5 variables u, v, x, y, z.
- Avant permutation :
u, v, x, y, z = 1, 2, 3, 4, 5- Après permutation :
u, v, x, y, z = 2, 3, 4, 5, 1
u, v, x, y, z = 1, 2, 3, 4, 5tmp = uu = vv = xx = yy = zz = tmp
| /0/: | On commence par initialiser les variables. |
|---|---|
| /1/: | Après l'initialisation des variables, on sauvegarde une des valeurs initiales dans une variable temporaire. |
En utilisant les n-uplets de Python, on aurait pu écrire plus directement:
u, v, x, y, z = 1, 2, 3, 4, 5
u, v, x, y, z = v, x, y, z, u
Les exemples précédents de séquences d'affectation illustrent la possibilité de réaliser des calculs plus ou moins compliqués à l'aide d'une séquence d'affectations bien choisies. Mais ce sont les alternatives et les itérations qui permettront d'aborder des algorithmes plus complexes, tout en améliorant l'expressivité des programmes.