Fichier de rejeu Close
Indication Close
A propos de... Close
Commentaire Close
Algorithmique - Cours
- Objectif 4: définition
- Objectif 5: appels
- Objectif 6: récursivité
Téléchargements

Aide
Récursivité
Définir et utiliser ses propres fonctions récursives dans le cadre du langage Python.
Les éléments de cours sont développés dans les 2 premières sections, les exercices associés dans la dernière section.
Appels récursifs
Définitions
La suite des nombres \(u_n\) de Fibonacci est définie par la relation de récurrence suivante :
La relation de récurrence exprime le nombre \(u_n\) à l'ordre n en fonction des nombres \(u_{n-1}\) et \(u_{n-2}\), respectivement à l'ordre \((n-1)\) et \((n-2)\). Ainsi, on définit \(u_n\) directement en fonction de \(u_{n-1}\) et de \(u_{n-2}\). Cette écriture est très compacte et très expressive; en particulier, elle ne fait pas intervenir de boucle comme dans le code de la fonction déjà rencontré dans la définition d'une fonction.
Il serait donc intéressant de définir la fonction
fibonacci de manière aussi simple dans le langage
algorithmique qu'en mathématiques. Cela nécessite de pouvoir définir
une fonction en l'appelant elle-même : on parle alors de
récursivité
ou de récursion.
1. Version itérative
def fibonacci(n) :
u, u1, u2 = 1, 1, 1
for i in range(2,n+1) :
u = u1 + u2
u1, u2 = u, u1
return u
On retrouve ici la version itérative déjà proposée comme exemple de définition d'une fonction.
2. Version récursive
def fibonacci(n) :
if n <= 1 :
u = 1
else :
u = fibonacci(n-1) + fibonacci(n-2)
return u
Cette version est dite « récursive » parce que
dans le corps de la fonction fibonacci, on appelle la fonction
fibonacci elle-même, et on l'appelle même 2 fois.
Cette version récursive est la traduction directe
de la formulation mathématique.
Une fonction est dite récursive si elle s'appelle elle-même : on parle alors d'appel récursif de la fonction.
Dans la version récursive, pour calculer fibonacci(5),
on calcule d'abord fibonacci(4) et fibonacci(3).
Pour calculer fibonacci(4),
on calcule fibonacci(3) et fibonacci(2).
Pour calculer fibonacci(3), on calcule fibonacci(2) et fibonacci(1)...
Le déroulement du processus est arborescent comme le montre
la figure ci-dessous.
On remarque
que les branches de l'arbre se divise en deux à chaque niveau
(sauf en bas de l'arbre, ie. à droite sur la figure),
ce qui traduit le fait que la fonction fibonacci s'appelle elle-même deux fois
à chaque fois qu'elle est invoquée avec \(n > 1\).
Dans cet arbre, on constate par exemple que
le calcul de fibonacci(3) est développé intégralement 2 fois :
une fois pour le
calul de fibonacci(4) et une fois pour lui-même.
En fait, il n'est pas très difficile de montrer que le nombre
de fois où la fonction calcule fibonacci(1) ou fibonacci(0)
(ie. le nombre de feuilles dans l'arbre) est précisément
\(u_n\) (fibonacci(n)).
Or la valeur de \(u_n\) croît de manière exponentielle avec \(n\);
ainsi, avec cette version récursive, le processus de calcul de fibonacci(n)
prend un temps qui croît de façon exponentielle avec \(n\).
Dans la version itérative, on ne passe que \((n-1)\) fois dans la boucle.
Ainsi, le processus de calcul itératif de fibonacci(n)
prend un temps qui croît de manière linéaire avec \(n\).
La différence entre les temps de calcul requis par les 2 méthodes,
l'une linéaire en \(n\) et l'autre augmentant aussi vite que \(u_n\)
lui-même, est donc énorme même pour de petites valeurs de \(n\).
Par exemple, pour \(n = 50\),
il faudra 50 unités de temps pour la méthode itérative contre 20365011074
(plus de 20 milliards unités de temps !)
pour la méthode récursive. La version itérative sera donc préférée
à la version récursive dans ce cas là : « il n'y a pas photo » !
Il ne faudrait pas conclure à l'inutilité des processus récursifs en arbre.
Pour les processus opérant sur des structures de données hiérarchiques et
non plus sur des nombres, la récursivité en arbre est un outil naturel et
puissant.
Même pour les calculs numériques, les processus récursifs en arbre
peuvent être utiles à la compréhension et à la conception d'algorithmes.
Par exemple, bien que la version récursive de fibonacci soit beaucoup moins
efficace que la version itérative, elle s'obtient presque directement,
étant à peine plus qu'une traduction en Python de la définition mathématiques
des nombres de Fibonacci.
En revanche, pour formuler la version itérative, il fallait avoir remarqué
que le calcul pouvait être revu sous la forme d'une itération avec 3 variables;
ce qui est bien moins direct et moins intuitif que la version récursive.
Grands classiques
Factorielle
La fonction factorielle qui calcule le produit des \(n\) premiers entiers positifs \(\displaystyle \left(n! = \prod_{k=1}^n k\right)\) est simplement définie par la relation de récurrence :
1. Version itérative
def factorielle(n) :
u = 1
for i in range(2,n+1):
u = i * u
return u
On retrouve ici la version itérative bien connue.
2. Version récursive
def factorielle(n) :
if n <= 1 :
u = 1
else :
u = n * factorielle(n-1)
return u
Cette version est dite « récursive » parce que
dans le corps de la fonction factorielle, on appelle la fonction
factorielle elle-même.
Cette version récursive est la traduction directe
de la formulation mathématique.
Dans la version récursive, le processus nécessite que l'interpréteur garde une trace des multiplications à réaliser plus tard. Le processus croît puis décroît : la croissance se produit lorsque le processus construit une chaîne d'opérations différées (ici, une chaîne de multiplications différées) et la décroissance intervient lorsqu'on peut évaluer les multiplications. Ainsi, la quantité d'information qu'il faut mémoriser pour effectuer plus tard les opérations différées croît linéairement avec \(n\) : on parle de processus récursif linéaire.
 python : recursivite-factorielle-1.py
python : recursivite-factorielle-1.py
L'interprétation d'une fonction récursive passe donc par une phase
d'expansion dans lesquels les appels récursifs sont « empilés » jusqu'à
arriver à un appel de la fonction pour lequel une condition d'arrêt sera
vérifiée, puis par une phase de contraction dans laquelle les résultats
des appels précédemment empilés sont utilisés.
Par contre, dans la version itérative, le processus de calcul ne croît ni
ne décroît : à chaque étape, seules les valeurs courantes des variables
u et i sont nécessaires (il n'y a pas d'opérations différées)
et le temps requis pour calculer \(n!\) augmente linéairement avec \(n\)
(on passe \((n-2)\) fois dans la boucle).
Tours de Hanoï
Les « tours de Hanoï » est un jeu imaginé par le mathématicien français Édouard Lucas (1842-1891). Il consiste à déplacer \(n\) disques de diamètres différents d'une tour de « départ » à une tour d'« arrivée » en passant par une tour « intermédiaire » et ceci en un minimum de coups, tout en respectant les règles suivantes :
- on ne peut déplacer qu'un disque à la fois,
- on ne peut placer un disque que sur un autre disque plus grand que lui ou sur une tour vide.
Dans l'état initial, les \(n\) disques sont placés sur la tour « départ ». Dans l'état final, tous les disques se retrouvent placés dans le même ordre sur la tour « arrivée ».
On cherche donc à définir une procédure
hanoi(n,depart,intermediaire,arrivee) qui devra déplacer
n disques de la tour depart à la tour arrivee
en utilisant la tour intermediaire comme tour de
transit.
Numérotons \(1,2,3,\ldots,n\) les \(n\) disques du plus
petit (numéro \(1\)) au plus grand (numéro \(n\)). A un moment donné,
dans la suite des opérations à effectuer, il faudra déplacer le disque
numéro \(n\) (le plus grand, placé initialement en dessous de la
pile de disques) de la tour « départ » à la tour « arrivée ».
Pour pouvoir effectuer ce déplacement, il faut d'une part qu'il n'y ait plus
aucun disque sur le disque \(n\) et d'autre part que la tour « arrivée »
soit vide;
en conséquence, il faut que tous les autres disques (de \(1\) à \((n-1)\)) soient
sur la tour « intermédiaire ». Pour atteindre cet état
intermédiaire (noté a sur la figure ci-dessous), il faut donc déplacer les \((n-1)\) premiers disques de la tour
« départ » à la tour « intermédiaire » en utilisant la tour « arrivée » comme
tour de transit : ce déplacement correspond à l'appel
hanoi(n-1,depart,arrivee,intermediaire). Une fois réalisé ce déplacement
des \((n-1)\) premiers disques, le disque \(n\) peut être déplacé de la tour « départ »
à la tour « arrivée » (état intermédiaire b sur la figure ci-dessous).
Il ne reste plus qu'à déplacer les \((n-1)\) premiers disques de la tour
« intermédiaire » à la tour « arrivée » en utilisant la tour « départ » comme
tour de transit; ces derniers déplacements correspondent
à l'appel hanoi(n-1,intermediaire,depart,arrivee).
On en déduit l'implémentation de la procédure hanoi ci-dessous
où le déplacement y est traduit par un simple affichage du type :
déplacer disque 3 de la tour « départ » à la tour « arrivée ».
python : recursivite-hanoi.pyOutputpython : recursivite-hanoi-scope.py
L'exécution d'un appel à la procédure hanoi s'apparente ici encore
à un processus récursif en arbre : les 7 déplacements effectués lors
de l'appel hanoi(3,'d','i','a') sont numérotés dans leur ordre d'apparition
sur la figure ci-dessous (les appels à la fonction hanoi
pour \(n = 0\) ne font rien : instruction pass).
Mais toutes les fonctions récursives ne
conduisent pas nécessairement à un processus récursif en arbre
comme l'exemple de la fonction factorielle le montre.
Méthode par récurrence
Exemples
Les exemples des fonctions factorielle et fibonacci présentent
certaines similarités :
les nombres \(n!\) et \(fibo(n)\) sont les éléments de suites numériques définies par récurrence : une suite définie par récurrence est une suite définie par son premier terme et par une relation de récurrence, qui définit chaque terme à partir du précédent ou des précédents lorsqu'ils existent.
suite factorielle fibonacci premier(s) terme(s) \(u_0 = 1\) \(u_0 = u_1 = 1\) relation de récurrence \(u_n = nu_{n-1}\) \(u_n = u_{n-1} + u_{n-2}\) les algorithmes récursifs les concernant commencent par tester le premier terme :
algorithme factorielle fibonacci premier(s) terme(s) \(0! = 1\)
if n <= 1 : u = 1\(u_0 = u_1 = 1\)
if n <= 1 : u = 1Pour ce premier terme, la valeur de du résultat est connue : il n'y a pas besoin de faire un appel récursif.
puis, s'il ne s'agit pas du premier terme, ces algorithmes font un appel récursif correspondant à la relation de récurrence de leur définition respective :
algorithme factorielle fibonacci relation de récurrence \(n! = n (n-1)!\)
else : u = n * factorielle(n-1)\(u_n = u_{n-1} + u_{n-2}\)
else : u = fibonacci(n-1) + fibonacci(n-2)L'appel récursif peut être simple comme pour la fonction
factorielleou multiple comme pour la fonctionfibonacci.Dans tous les cas, c'est le traitement du cas particulier que constitue le premier terme de la suite qui permet d'arrêter la chaîne des appels récursifs (
fappellefqui appellefqui appellefqui appelle ...). Il faut donc que l'appel récursif « se rapproche » progressivement du cas particulier. C'est bien le cas des fonctionsfactorielleetfibonacci:
algorithme factorielle fibonacci relation de récurrence \(n! = n (n-1)!\) \(u_n = u_{n-1} + u_{n-2}\) évolution de la récursivité au fur et à mesure qu'on appelle n * factorielle(n-1), \(n\) diminue et sa valeur tend vers 0 qui est le cas particulier connu (\(0! = 1\))au fur et à mesure qu'on appelle u = fibonacci(n-1) + fibonacci(n-2), \(n\) diminue et sa valeur tend vers 1 ou 0 qui sont les cas particuliers connus (\(u_0 = u_1 = 1\))
Méthode
La méthode par récurrence s'inspire des exemples précédents pour définir la structure d'une fonction récursive.
- Dans un premier temps, on identifie le (ou les) cas particulier(s) pour le(s)quel(s) on connaît une solution au problème.
- Dans un deuxième temps, on précise la relation de récurrence qui fera progresser l'algorithme vers le(s) cas particulier(s); ce qui arrêtera la chaîne des appels récursifs.
La structure d'une fonction récursive est donc du type:
def f(x) :
# cas particulier(s)
if x == val :
# traitement direct du cas particulier
# pas d'appel récursif
# appel(s) récursif(s)
else :
# traitement de(s) appel(s) récursif(s)
# relation de récurrence
Ainsi en va-t-il bien sûr pour les fonctions factorielle et fibonacci :
méthode par récurrence factorielle fibonacci cas particulier(s) appel(s) récursif(s)
Et la fonction hanoi(n,gauche,milieu,droite) précédemment rencontrée
présente également cette même structure :
méthode par récurrence hanoi cas particulier appels récursifs
Formes de récursivité
On distingue classiquement 4 grandes formes de récursivité : simple, imbriquée, multiple et croisée.
Un appel récursif est dit simple si la fonction ne contient qu'un seul appel récursif à elle-même.
Un exemple classique de récursivité simple est celui de la fonction factorielle définie mathématiquement par :
\[\left\{\begin{array}{llll} 0! &=& 1 & \\ n! &=& n\cdot (n-1)! & \forall n \in \mathbb{N}^* \end{array}\right.\]python : recursivite-simple.pyOutputpython : recursivite-simple.py
Un appel récursif est dit imbriqué si l'appel récursif a comme argument un autre appel récursif à la même fonction.
Un exemple classique de récursivité imbriquée est celui de la fonction de MacCarthy définie mathématiquement par :
\[\left\{\begin{array}{llll} f(n) &=& n - 10 & \{n \in \mathbb{N}|\ n > 100\}\\ f(n) &=& f(f(n+11)) & \{n \in \mathbb{N}|\ n \leq 100\} \end{array}\right.\]python : recursivite-imbriquee.pyOutputpython : recursivite-imbriquee.py
Un appel récursif est dit multiple si la fonction contient plusieurs appels récursifs à elle-même.
Un exemple classique de récursivité multiple est celui de la fonction de Fibonacci définie mathématiquement par :
\[\left\{\begin{array}{llll} f(0) &=& 1 & \\ f(1) &=& 1 & \\ f(n) &=& f(n-1) + f(n-2) & \{n \in \mathbb{N}|\ n > 1\} \end{array}\right.\]python : recursivite-multiple.pyOutputpython : recursivite-multiple.py
Les tours de Hanoï sont un autre exemple bien connu de récursivité multiple.
Un appel récursif est dit croisé si 2 fonctions récursives s'appellent mutuellement.
Un exemple classique de récursivité croisée est celui des fonctions de parité
even (pair) et odd (impair) définies mathématiquement par :
\[\left\{\begin{array}{llll} even(0) &=& 1 & \\ even(n) &=& odd(n-1) & \forall n \in \mathbb{N}^* \end{array}\right.\]\[\left\{\begin{array}{llll} odd(0) &=& 0 & \\ odd(n) &=& even(n-1) & \forall n \in \mathbb{N}^* \end{array}\right.\]python : recursivite-croisee.pyOutputpython : recursivite-croisee.py
Récursion versus Itération
Processus récursif ou processus itératif
Lorsqu'on parle de fonction récursive, on fait référence à une
caractéristique syntaxique : la fonction, dans sa propre définition,
fait réfèrence à elle-même (elle s'appelle elle-même).
Mais lorsqu'on parle de processus récursif, linéaire ou en arbre,
on s'intéresse au déroulement du processus, et non à la syntaxe de
l'écriture de la fonction.
Ainsi, une fonction peut avoir une définition récursive mais correspondre à
un processus itératif : c'est le cas de la nouvelle version de la fonction
factorielle ci-dessous.
def factorielle(n): u = factIter(n,1,1) return u def factIter(n,i,fact): if i < n: return factIter(n,i+1,fact*(i+1)) else : return fact
La nouvelle fonction factorielle appelle une fonction
auxiliaire factIter dont la définition est syntaxiquement récursive
(factIter s'appelle elle-même). Cette fonction à 3 arguments : l'entier n
dont il faut calculer la factorielle, un compteur i initialisé à 1
au premier appel de factIter par factorielle et incrémenté à chaque
nouvel appel, et un nombre fact initialisé à 1 et multiplié
par la nouvelle valeur du compteur à chaque nouvel appel.
 python : recursivite-factorielle-2.py
python : recursivite-factorielle-2.py
Le déroulement
d'un appel à factIter montre qu'ainsi, à chaque étape, la relation
(i! == fact) est toujours vérifiée. La fonction factIter
arrête de s'appeler elle-même lorsque (i == n) et on a alors
(fact == i! == n!) qui est la valeur recherchée. Ainsi, à chaque étape,
nous n'avons besoin que des valeurs courantes du compteur i
et du produit fact,
exactement comme dans la version itérative de la fonction factorielle :
il n'y a plus de chaîne d'opérations différées comme dans la version récursive
de factorielle. Le processus mis en jeu ici est un processus itératif,
bien que la définition de factIter soit récursive.
Dans la fonction factIter, le résultat de l'appel récursif est
retourné par la fonction : on parle alors de récursivité terminale
(ou récursivité à droite).
L'exécution d'un tel appel termine l'exécution de la fonction.
Un appel récursif terminal est un appel récursif dont le résultat est celui retourné par la fonction.
En d'autres termes, si dans le corps d'une fonction, un appel récursif est placé de telle façon que son exécution n'est jamais suivi par l'exécution d'une autre instruction de la fonction, cet appel est dit récursif à droite. Si ce n'est pas le cas, on parle de récursivité non terminale ou de récursivité à gauche.
Un appel récursif non terminal est un appel récursif dont le résultat n'est pas celui retourné par la fonction.
Dérécursivation
Quel que soit le problème à résoudre, on a le choix entre l'écriture
d'une fonction itérative et celle d'une fonction récursive.
Si le problème admet une structure récurrente naturelle,
le programme récursif est alors une simple adaptation de la structure
choisie. C'est le cas des fonctions factorielle et
fibonacci par exemple.
L'approche récursive présente cependant des inconvénients :
certains langages n'admettent pas la récursivité (comme le langage machine !)
et elle est souvent coûteuse en mémoire comme en temps d'exécution.
On peut pallier ces inconvénients en transformant la fonction récursive
en fonction itérative : c'est toujours possible.
Récursivité terminale
2 Du récursif terminal à l'itératif1. Version récursive
Considérons une fonction f à récursivité terminale:
def f(x):
if cond:
return stop
else:
instructions
return f(g(x))
return
x représente ici la liste des arguments de la fonction,
cond une condition portant sur x,
instructions un bloc d'instructions qui constituent
le traitement de base de la fonction f et qui ne contient pas d'appel
récursif à f,
g(x) une transformation des arguments et stop
l'instruction de terminaison (clause d'arrêt) de la récurrence.
2. Version itérative
La version récursive est équivalente à la fonction itérative suivante:
def f(x):
while not cond:
instructions
x = g(x)
return stop
Illustrons cette transformation à l'aide de la fonction qui calcule le pgcd
de 2 entiers:
def pgcd(a,b):
if b == 0 :
return a
else:
pass
return pgcd(b,a%b)
On a les correspondances suivantes :
fpgcdxa,bcondb == 0return stopreturn ainstructions passg(x)b,a%b
d'où la version itérative du pgcd:
def pgcd(a,b):
while not (b == 0):
pass
a,b = b,a%b
return a
La méthode générique précédente ne s'applique qu'à la récursivité terminale. Ceci étant, la plupart des compilateurs aujourd'hui reconnaissent une récursivité terminale et savent la transformer automatiquement en boucle. Ce n'est pas aussi simple avec une récursivité non terminale.
Récursivité non terminale
Une méthode générale existe pour transformer une fonction récursive quelconque en une fonction itérative équivalente. En particulier, elle est mise en œuvre dans les compilateurs car le langage machine n'admet pas la récursivité. Cette méthode générale fait appel à la notion de pile pour sauvegarder le contexte des appels récursifs.
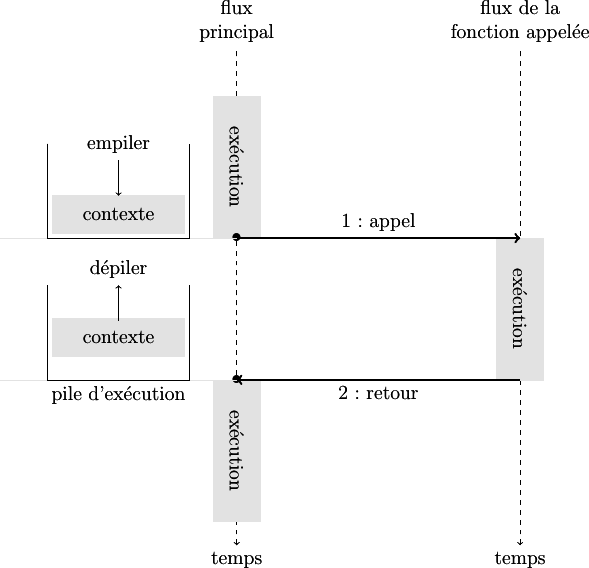
Pile d'exécution
Un programme est un flux d'instructions exécutées séquentiellement.
Lors de l'appel d'une fonction, ce flux est interrompu le temps de l'exécution de cette fonction, avant de reprendre à l'endroit où le programme s'est arrêté. A l'interruption, le processeur sauvegarde un certain nombre de données qui forment le contexte de l'appel. Ce contexte est stocké dans une pile : la pile d'exécution. Au retour de la fonction, le contexte est dépilé pour être rétabli et permettre la poursuite de l'exécution du programme.
Lors de l’exécution d’une fonction récursive, chaque appel récursif conduit à un empilement du contexte dans la pile d’exécution. Lorsque se produit la condition d’arrêt de la récursivité, les différents contextes sont progressivement dépilés pour poursuivre l’exécution de la fonction.
Illustrons le fonctionnement de la pile d'exécution avec l'exemple des tours de Hanoï.
Version itérative des tours de Hanoï
Nous allons simuler le fonctionnement d'une pile d'exécution.
On commence par créer la pile d'exécution, représentée ici par une liste:
pile = []
On définit le contexte appelant par un n-uplet
(n,gauche,milieu,droite,"appel")
composé des 4 paramètres d'entrée de la fonction et d'un dernier
paramètre "appel", une simple chaîne de caractères
qui rappelle qu'il s'agit de l'appel de la fonction:
contexte = (n,gauche,milieu,droite,"appel")
On empile ce contexte dans la pile d'exécution:
pile.append(contexte)
Tant que la pile d'exécution n'est pas vide:
while pile != [] :
on exécute alors l'algorithme suivant :
On récupère le contexte en dépilant la pile:
(n,gauche,milieu,droite,etat) = pile.pop()S'il y a des disques à déplacer (
if n > 0 :) on teste s'il s'agit d'un appel (etat == "appel") ou d'un retour ("retour") de fonction:if (etat == "appel") : # 2.1 else : # 2.2
- 2.1 S'il s'agit d'un appel (
etat == "appel"), on commence parempiler l'état courant en attendant le retour de la fonction:
pile.append((n,gauche,milieu,droite,"retour"))puis on empile le premier appel récursif:
pile.append((n-1,gauche,droite,milieu,"appel"))- 2.2 S'il s'agit d'un retour (
etat == "retour") de la fonction,on poursuit l'exécution de l'algorithme par le déplacement du disque
ndegaucheàdroite:deplacer(n,gauche,droite)puis par le deuxième appel récursif:
pile.append((n-1,milieu,gauche,droite,'appel'))
On obtient ainsi une version itérative des tours de Hanoï qui n'aurait
pas été simple à trouver sans passer par la version récursive.
Le programme suivant permet d'illustrer les 2 exécutions : la récursive
(hanoi_recursif) et l'itérative (hanoi_iteratif).
python : recursivite-hanoi-iteratif.pyOutput