Contexte informatique

Définition

Le terme informatique est un néologisme proposé en 1962 par Philippe Dreyfus (informaticien français né en 1930) pour caractériser le traitement automatique de l'information : il est construit sur la contraction de l'expression « information automatique ». Il s'agit d'une traduction de l'allemand « informatik » proposé dès 1957 par Karl Steinbuch (informaticien allemand, 1917-2005). Ce terme a été accepté par l'Académie française en avril 1966, et l'informatique devint alors officiellement la science du traitement automatique de l'information, où l'information est considérée comme le support des connaissances humaines et des communications dans les domaines techniques, économiques et sociaux.

Le mot « informatique » n'a pas vraiment d'équivalent aux Etats-Unis où l'on parle de Computing Science (science du calcul) alors que Informatics est admis par les Britanniques et informática par les Espagnols.

L'informatique traite de deux aspects complémentaires : les programmes immatériels (logiciel, software) qui décrivent un traitement à réaliser et les machines (matériel, hardware) qui exécutent ce traitement. Le matériel est donc l'ensemble des éléments physiques (microprocesseur, mémoire, écran, clavier, disques durs...) utilisés pour traiter les données. Dans ce contexte, l'ordinateur est un terme générique qui désigne un équipement informatique permettant de traiter des informations selon des séquences d'instructions (les programmes) qui constituent le logiciel. Le terme « ordinateur » a été proposé en 1955 par Jacques Perret (philologue français, 1906-1992) en réponse à une demande d'IBM France qui estimait le mot « calculateur » (computer) bien trop restrictif en regard des possibilités de ces machines.

Ordinateur

Un ordinateur n'est rien d'autre qu'une machine effectuant des opérations simples sur des séquences de signaux électriques. Ces séquences de signaux obéissent à une logique binaire du type « tout ou rien » (« vrai ou faux ») et peuvent donc être considérés comme des suites de nombres ne prenant jamais que les deux valeurs 0 (faux, false) et 1 (vrai, true) : les chiffres binaires (bit : binary digit). Un ordinateur est donc incapable de traiter autre chose que des nombres binaires et toute information d'un autre type doit être convertie, ou codée, en format binaire. C'est vrai non seulement pour les données que l'on souhaite traiter (les nombres, les textes, les images, les sons, les vidéos, etc...), mais aussi pour les programmes, c'est-à-dire les séquences d'instructions que l'on va fournir à la machine pour lui dire ce qu'elle doit faire avec ces données.

Dès 1936, Alan Turing (mathématicien anglais, 1912-1954) imagine une machine universelle conceptuelle capable d'exécuter tout algorithme : la machine de Turing. Le premier calculateur électromécanique à base de relais conforme à la machine de Turing, le Z3 conçu par Konrad Zuse (ingénieur allemand, 1910-1995), date de 1941. Quant au premier calculateur entièrement électronique à base de tubes à vide conforme à la machine de Turing, l'ENIAC (Electronic Numerical Integrator Analyser and Computer) conçu par Presper Eckert (ingénieur américain, 1919-1995) et John Mauchly (physicien américain, 1907-1980), il voit le jour en 1946.

Z3 (1941)	ENIAC (1946)

Les premiers micro-ordinateurs apparaissent dans les années 1970-1980 :

Micral (1973)	Commodore PET 2001 (1977)	Apple II (1977)	Sinclair ZX81 (1981)	IBM PC (1981)	Apple Macintosh (1984)

Aujourd'hui, les ordinateurs conforme à la machine de Turing avec l'architecture de Von Neumann prennent de nombreuses formes :

bureau	portable	tablette	console de jeux	smartphone	montre

L'architecture matérielle d'un ordinateur repose sur le modèle de Von Neumann (physicien hongrois, 1903-1957) qui distingue classiquement 4 parties :

• l'unité arithmétique et logique, ou unité de traitement, effectue les opérations de base ;
• l'unité de contrôle séquence les opérations.
• La mémoire contient à la fois les données et le programme qui dira à l'unité de contrôle quels calculs faire sur ces données; elle se divise entre mémoire vive volatile (programmes et données en cours de fonctionnement) et mémoire de masse permanente (programmes et données de base de la machine) ;
• les entrées-sorties sont des dispositifs permettant de communiquer avec le monde extérieur (écran, clavier, souris, réseau...).

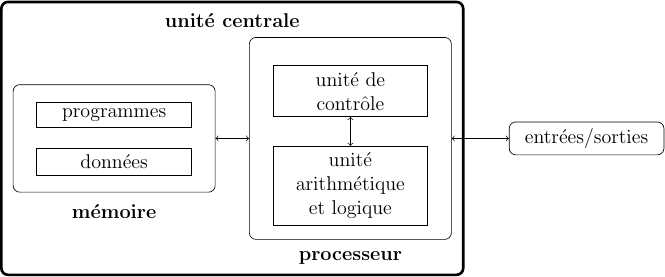
Les 2 premières parties sont souvent rassemblées au sein d'une même structure : le processeur (la « puce »). Le processeur et la mémoire constituent l'unité centrale d'un ordinateur. La carte-mère est le support de l'unité centrale et des ports de connexion de l'ordinateur.

Processeur	Mémoire	Carte-mère

Périphériques

Les périphériques sont des dispositifs matériels qui permettent à l'ordinateur de communiquer avec l'extérieur.

• Les périphériques d'entrée envoient des informations vers l'ordinateur : clavier, souris, tablette graphique, micro, caméra, scanneur, manette de jeu, lecteur CD (Compact Disc), lecteur DVD (Digital Versatile Disc)...
• Les périphériques de sortie récupèrent des informations issus de l'ordinateur : écran, haut-parleur, imprimante, graveur CD/DVD...
• Les périphériques d'entrée-sortie fonctionnent dans les deux sens : écran tactile, imprimante-scanneur, lecteur-graveur CD/DVD...
• Les périphériques de stockage jouent le rôle de mémoire permanente en conservant des informations issues de la mémoire de l'ordinateur : disque dur interne ou externe, clé USB (Universal Serial Bus), disque CD/DVD, carte mémoire SD (Secure Digital), carte mémoire SIM (Subscriber Identity Module)...
• Les périphériques réseau permettent de transmettre les informations sur de très longues distances le plus souvent selon un protocole ethernet sur paires torsadées, fibres optiques ou sans fil (wifi) : modem, commutateur (switch), routeur, concentrateur (hub)...

Les périphériques sont connectés à l'ordinateur ou entre eux via différents ports de connexion selon le périphérique :

Connecteur	Port	Cable	Périphériques
Audio			haut-parleurs, microphones, casques
DVI Digital Visual Interface			écrans
Ethernet			périphériques réseau
HDMI High Definition Multimedia Interface			périphériques multimédias numériques
USB Universal Serial Bus			clés USB, disques durs, souris, claviers, caméras, imprimantes...
VGA Video Graphics Array			écrans et vidéoprojecteurs analogiques

Définition

Exemple : Mode d'emploi d'un télécopieur

Extrait du mode d’emploi d’un télécopieur concernant l’envoi d’un document :

1. Insérer le document dans le chargeur automatique.
2. Composer le numéro de fax du destinataire à l'aide du pavé numérique.
3. Enfoncer la touche « envoi » pour lancer l'émission.

Ce mode d'emploi précise comment envoyer un fax. Il est composé d'une suite ordonnée d'instructions (insérer..., composer..., enfoncer...) qui manipulent des données (document, chargeur automatique, numéro de fax, pavé numérique, touche « envoi ») pour réaliser la tâche désirée (envoi d'un document). Chacun a déjà été confronté à de tels documents pour faire fonctionner un appareil et donc, consciemment ou non, a déjà exécuté un algorithme (ie. exécuter la suite d'instructions dans l'ordre annoncé par le mode d'emploi).

Le mot algorithme vient du nom simplifié (Al-Khawarizmi) et latinisé (algoritmi) d’un mathématicien Perse, Abu Abdallah Muhammed Ibn Mussa Al-Khawarizmi, né vers 783 et mort vers 850 à Bagdad.

Dans ce dialogue, la réponse de l'autochtone est la description d'une suite ordonnée d'instructions (allez tout droit, prenez à gauche, prenez la troisième à droite) qui manipulent des données (carrefour, rues) pour réaliser la tâche désirée (aller à la gare). Ici encore, chacun a déjà été confronté à ce genre de situation et donc, consciemment ou non, a déjà construit un algorithme dans sa tête (ie. définir la suite d'instructions pour réaliser une tâche). Mais quand on définit un algorithme, celui-ci ne doit contenir que des instructions compréhensibles par celui qui devra l'exécuter (des humains dans les 2 exemples précédents).

C’est le mathématicien anglais Alan Turing (1912-1954) qui formalisa le premier calculateur programmable avec sa machine abstraite, dite machine de Turing, ainsi que les concepts d’algorithme et de calculabilité à l’origine de la science des algorithmes : l’algorithmique.

Propriétés

L'algorithmique s'intéresse à l'art de construire des algorithmes ainsi qu'à caractériser leurs principales propriétés : validité, robustesse, réutilisabilité, complexité ou efficacité.

Validité

En premier lieu, on se posera toujours la question suivante : est-on certain que l’algorithme proposé réponde au problème pour lequel il a été conçu initialement ? En d’autres termes : est-il valide ?

Si l'on reprend l'exemple de l'algorithme de recherche du chemin de la gare, l'étude de sa validité consiste à s'assurer qu'on arrive effectivement à la gare en exécutant scrupuleusement les instructions dans l'ordre annoncé.

Robustesse

Dans tous les cas, un algorithme ne répondra au problème pour lequel il a été conçu que s’il vérifie certaines conditions d’utilisation : il n’est effectivement valide que sous ces conditions. Que se passe-t-il alors si ces conditions ne sont pas respectées ? En d’autres termes : est-il suffisamment robuste ?

Dans l’exemple du touriste égaré, la question de la robustesse de l’algorithme se pose par exemple si le chemin proposé a été pensé pour un piéton, alors que le touriste égaré est en voiture et que la « troisième à droite » est en sens interdit.

Réutilisabilité

Un algorithme, valide et robuste, peut n’avoir été conçu que pour rendre compte d’un problème particulier de manière tout à fait ad hoc, sans possibilité de généralisation. En d’autres termes : est-il réutilisable ?

L’algorithme de recherche du touriste égaré est-il réutilisable tel quel pour se rendre à la mairie ? A priori non, sauf si la mairie est juste à côté de la gare.

Complexité

L’algorithme peut être à priori valide, robuste et réutilisable, mais nécessiter des ressources (trop ?) importantes pour s’exécuter dans son contexte normal d’utilisation. Ces ressources peuvent concerner le temps mis, l’espace occupé ou l’énergie dépensée pour s’exécuter. En d’autres termes : quelle est sa complexité ?

Si le touriste égaré est un piéton, la complexité de l’algorithme de recherche de chemin peut se compter en nombre de pas pour arriver à la gare.

Efficacité

En dernier lieu, et seulement lorsque l’algorithme proposé a été validé, rendu robuste et réutilisable pour une complexité raisonnable, peut-on l’optimiser soit en diminuant sa complexité, soit en améliorant son contexte d’exécution ? En d’autres termes : quelle est son efficacité ?

Si notre touriste égaré est un piéton, n’existerait-il pas un raccourci piétonnier qui lui permette d’arriver plus vite à la gare ?

L’algorithmique permet ainsi de passer d’un problème à résoudre à un algorithme qui décrit la démarche de résolution du problème de manière valide et robuste, plus ou moins réutilisable, plus ou moins complexe et plus ou moins efficace selon son contexte d’exécution. La programmation a alors pour rôle de traduire cet algorithme dans un langage « compréhensible » par l’ordinateur afin qu’il puisse exécuter l’algorithme automatiquement.

Définition

Un algorithme exprime la structure logique d’un programme informatique et de ce fait est indépendant du langage de programmation utilisé. Par contre, la traduction de l’algorithme dans un langage particulier dépend du langage choisi et sa mise en œuvre dépend également de la plateforme d’exécution. L'exécution automatique du programme sur une machine réelle fournit un résultat qui correspond à la mise en œuvre du programme qui est lui-même la traduction dans un langage particulier d'un algorithme censé répondre au problème posé.

La programmation d’un ordinateur consiste à lui « expliquer » en détail ce qu’il doit faire, en sachant qu’il ne « comprend » pas le langage humain, mais qu’il peut seulement effectuer un traitement automatique sur des séquences de 0 et de 1. Un programme n’est rien d’autre qu’une suite d’instructions, encodées en respectant de manière très stricte un ensemble de conventions fixées à l’avance par un langage informatique. La machine décode alors ces instructions en associant à chaque « mot » du langage informatique une action précise. Le programme que nous écrivons dans le langage informatique à l’aide d’un éditeur (une sorte de traitement de texte spécialisé) est appelé programme source (ou code source).

Le seul « langage » que l’ordinateur puisse véritablement « comprendre » est donc très éloigné de ce que nous utilisons nous-mêmes. C’est une suite de 0 et de 1 (les bits, binary digit) traités par groupes de 8 (les octets, byte), 16, 32 ou 64.

Traduction

Pour « parler » à un ordinateur, il nous faudra donc utiliser des systèmes de traduction automatiques, capables de convertir en nombres binaires des suites de caractères formant des mots-clés (anglais en général) qui seront plus significatifs pour nous. Le système de traduction proprement dit s’appellera interpréteur ou bien compilateur, suivant la méthode utilisée pour effectuer la traduction. On appellera langage de programmation un ensemble de mots-clés (choisis arbitrairement) associé à un ensemble de règles très précises indiquant comment on peut assembler ces mots pour former des « phrases » que l’interpréteur ou le compilateur puisse traduire en langage machine (code binaire).

Compilation

La compilation consiste à traduire la totalité du code source en une fois. Le compilateur lit toutes les lignes du programme source et produit une nouvelle suite de codes appelé programme objet (ou code objet). Celui-ci peut désormais être exécuté indépendamment du compilateur et être conservé tel quel dans un fichier (« fichier exécutable »). Le code objet généré est spécifique du processeur qui exécutera le programme. Les langages Ada, C, Cobol et Fortran sont des exemples de langages compilés.

Interprétation

L’interprétation consiste à traduire chaque ligne du programme source en quelques instructions du langage machine, qui sont ensuite directement exécutées au fur et à mesure (« au fil de l’eau ») par le processeur. Aucun programme objet n’est généré. L’interpréteur doit être utilisé chaque fois que l’on veut faire fonctionner le programme : il se comporte comme le processeur d'une machine fictive (ou virtuelle) qui saurait exécuter directement les instructions du code source.

Les langages JavaScript, Lisp, Lua, Perl, Php, Prolog, Ruby et Sql sont des exemples de langages interprétés.

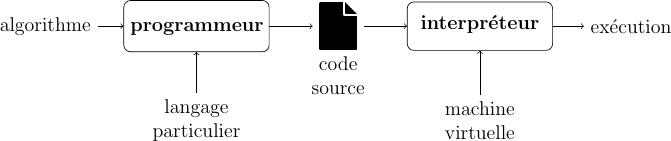
L’interprétation est idéale lorsque l’on est en phase d’apprentissage du langage, ou en cours d’expérimentation sur un projet. Avec cette technique, on peut en effet tester immédiatement toute modification apportée au programme source, sans passer par une phase de compilation qui demande toujours du temps. Mais lorsqu’un projet comporte des fonctionnalités complexes qui doivent s’exécuter rapidement, la compilation est préférable : un programme compilé fonctionnera toujours plus vite que son homologue interprété, puisque dans cette technique l’ordinateur n’a plus à (re)traduire chaque instruction en code binaire avant qu’elle puisse être exécutée.

Semi-compilation

Certains langages tentent de combiner les deux techniques afin d’en tirer le meilleur de chacune. C’est le cas des langages Python et Java par exemple. De tels langages commencent par compiler le code source pour produire un code intermédiaire, similaire à un langage machine (mais pour une machine virtuelle), que l’on appelle « bytecode », lequel sera ensuite transmis à un interpréteur pour l’exécution finale. Le bytecode utilise un jeu d'instruction d'une machine fictive (ou virtuelle). Il est conçu pour faire abstraction du jeu d'instruction final qui sera utilisé pour exécuter le programme sur le processeur de la machine réelle. Cette technique a été utilisée la première fois pour le langage Pascal dans les années 1970 (P-code) puis popularisée en 1995 par la machine virtuelle Java. Du point de vue de l’ordinateur, le bytecode est très facile à interpréter en langage machine. Cette interprétation est alors beaucoup plus rapide que celle d’un code source même si elle l'est moins que celle d’un véritable code machine, mais elle est satisfaisante pour de très nombreux programmes.

Le fait de disposer en permanence d’un interpréteur permet de tester immédiatement n’importe quel petit morceau de programme. On pourra donc vérifier rapidement le bon fonctionnement de chaque composant d’une application au fur et à mesure de sa construction.