Fichier de rejeu Close
Indication Close
A propos de... Close
Commentaire Close
Algorithmique - Cours
- Objectif 1: affectation
- Objectif 2: alternative
- Objectif 3: itération
Téléchargements
Aide
Itération
Présenter l'itération conditionnelle et la mettre en œuvre dans le cadre du langage Python.
Les éléments de cours sont développés dans les 3 premières sections, les exercices associés dans la dernière section.
Définition
Le plus grand commun diviseur de 2 entiers \(a\) et \(b\) peut se calculer en appliquant la relation de récurrence \(\mathrm{pgcd}(a,b) = \mathrm{pgcd}(b,a\%b)\) jusqu'à ce que le reste (\(a\%b\)) soit nul.
Ainsi, pour calculer le pgcd de \(a=12\) et de \(b=18\), on applique 3 fois de suite cette relation :
\(\mathrm{pgcd}(12,18) = \mathrm{pgcd}(18,12) = \mathrm{pgcd}(12,6) = \mathrm{pgcd}(6,0) = 6\).
L'algorithme correspondant fait donc apparaître 3 fois de suite les mêmes instructions après l'initialisation des variables \(a\) et \(b\) :
r = a%b
a, b = b, r
Si nous voulons maintenant calculer le pgcd de 44 et 5648, il nous faudra répéter 5 fois la même séquence d'instructions :
\(\mathrm{pgcd}(44,5648) = \mathrm{pgcd}(5648,44) = \mathrm{pgcd}(44,16) = \mathrm{pgcd}(16,12) = \mathrm{pgcd}(12,4) = \mathrm{pgcd}(4,0) = 4\).
Ce nouvel exemple soulève au moins 2 questions :
- Comment éviter de répéter explicitement plusieurs fois de suite la même séquence d'instructions ?
- Comment éviter de savoir à l'avance combien de fois il faut répéter la séquence pour obtenir le bon résultat ?
De nouvelles instructions de contrôle de flux sont introduites pour répondre à ces questions : les instructions itératives. On parle également de boucles, de répétitions ou encore d'itérations.
Boucle « while »
L'instruction while (tant que) permet de répéter plusieurs fois une
même instruction : le bloc d'instructions blocWhile est exécuté tant que
la condition est vérifiée. On arrête dès que la condition est fausse;
on dit alors qu'on « sort » de la boucle.
1 2 3 4 | instruction1
while condition :
blocWhile
instruction3
|
On commence par tester la condition; si elle
est vérifiée, on exécute le bloc d'instructions blocWhile
(encore appelé le « corps » de la boucle) puis on reteste la condition :
la condition est ainsi évaluée avant chaque exécution du corps
de la boucle; si la condition est à nouveau vérifiée on ré-exécute le bloc
d'instructions blocWhile (on dit qu'on « repasse » dans la boucle)
et ainsi de suite jusqu'à ce que la condition devienne fausse,
auquel cas on « sort » de la boucle.
L'itération conditionnelle est une instruction de contrôle du flux d'instructions qui permet sous condition préalable de répéter zéro ou plusieurs fois la même instruction.
Exemples
Le calcul du pgcd de 2 entiers peut se simplifier de la manière suivante :
while b != 0 : r = a%b a, b = b, r
python : iteration-pgcd.pyOutputOn cherche à écrire un algorithme qui affiche la table de multiplication d'un nombre \(n\) quelconque.
Exemple : \(n = 9\):
0 * 9 = 0 1 * 9 = 9 2 * 9 = 18 3 * 9 = 27 4 * 9 = 36 5 * 9 = 45 6 * 9 = 54 7 * 9 = 63 8 * 9 = 72 9 * 9 = 81
Cet affichage peut être obtenu par l'algorithme suivant :
python : iteration-table-multiplication-9.pyOutputDans une itération conditionnelle, la condition doit évoluer au cours des différents passages dans la boucle afin de pouvoir sortir de la boucle. C'est le cas de la boucle
whilede l'exemple ci-dessus; à chaque passage dans la boucle, le multiplicateuriest incrémenté : ainsi, partant de la valeur initialei = 0,ideviendra nécessairement égal à 10 après 10 passages dans la boucle.
Deux cas extrêmes
En ce qui concerne le nombre de passages dans la boucle, deux cas extrèmes peuvent se produire :
la condition n'est pas vérifiée la première fois : on ne passe alors jamais dans la boucle.
Exemple :
x = 4 y = 0 while x < 0 : y = y + x
xest positif; la conditionx < 0n'est donc pas vérifiée la première fois : on ne rentre pas dans la boucle.la condition n'est jamais fausse : on ne sort jamais de la boucle; on dit qu'on a affaire à une boucle « sans fin » ou à une boucle « infinie ».
Exemple :
x = 4 y = 0 while y >= 0 : y = y + x
yest initialement nul : on rentre dans la boucle; l'instruction du corps de la boucle ne peut qu'incrémenterypuisquexest positif (x = 4) :ysera donc toujours positif et on ne sortira jamais de la boucle.Le cas de la boucle « sans fin » est évidemment dû le plus souvent à une erreur involontaire qu'il faut savoir détecter assez vite pour éviter un programme qui « tourne » indéfiniment sans s'arrêter.
Empathie numérique
La maîtrise de l'algorithmique requiert deux qualités complémentaires :
- il faut avoir une certaine intuition, car aucun algorithme ne permet de savoir a priori quelles instructions permettront d'obtenir le résultat recherché. C'est là qu'intervient la forme « d'intelligence » requise pour l'algorithmique : la « créativité » de l'informaticien. Il y a des gens qui possèdent au départ davantage cette intuition que les autres. Cependant, les réflexes, cela s'acquiert (voir plus loin la méthode de l'invariant pour aider à construire des boucles) Et ce qu'on appelle l'intuition n'est finalement que de l'expérience accumulée, tellement répétée que le raisonnement, au départ laborieux, finit par devenir « spontané ».
- il faut être méthodique et rigoureux. En effet, chaque fois qu'on écrit une série d'instructions que l'on croit justes, il faut systématiquement se mettre mentalement à la place de la machine qui va les exécuter (sur papier ou dans sa tête) afin de vérifier si le résultat obtenu est bien celui que l'on voulait (méthode de l'empathie numérique déjà rencontrée ici et là). Cette opération ne requiert pas d'intuition. Mais elle reste néanmoins indispensable si l'on ne veut pas écrire des algorithmes à l'« aveuglette ». Et petit à petit, à force de pratique, on fera de plus en plus souvent l'économie de cette étape : l'expérience fera qu'on « verra » le résultat produit par les instructions, au fur et à mesure qu'on les écrira. Naturellement, cet apprentissage est long, et demande des heures de travail patient. Aussi, dans un premier temps, il faut éviter de sauter les étapes : la vérification méthodique, pas à pas, de chacun des algorithmes représente plus de la moitié du travail à accomplir... et le gage de progrès.
Exemples
Lire pour programmerDéterminer « à la main » les valeurs des variables
a,b,qetraprès la séquence d'affectations suivante :a, b = 19, 6 q, r = 0, a while r >= b : q = q + 1 r = r - b
A la fin de l'algorithme, l'instruction
print a,b,q,raffiche ?Déterminer « à la main » les valeurs des variables
a,betraprès la séquence d'affectations suivante :a, b = 12, 18 while b != 0 : r = a%b a, b = b, r
A la fin de l'algorithme, l'instruction
print a,b,raffiche ?
Indication
Textes à trous
| Bouton | Action |
|---|---|
| Initialiser toutes les zones de saisie | |
| Afficher cette aide | |
| Afficher le bilan de l'exercice |
| Clavier | Action |
|---|---|
| Enter | Valider la zone de saisie |
| F1 | Afficher une aide technique |
| F2 | Afficher une aide pédagogique |
| Ctrl-A | Tout sélectionner |
| Ctrl-C | Copier la sélection dans le presse-papier |
| Ctrl-V | Copier le presse-papier dans la sélection |
| Ctrl-X | Couper la sélection et la copier dans le presse-papier |
| Ctrl-Z | Annuler la modification |
| Maj-Ctrl-Z | Rétablir la modification |
| Question | Bilan |
|---|---|
| Nombre de trous | |
| Réponses non validées | |
| Réponses validées | |
| Taux de validation | |
| Réponses validées non attendues | |
| Réponses validées attendues | |
| Taux de réussite partiel | |
| Taux de réussite total |
Méthode
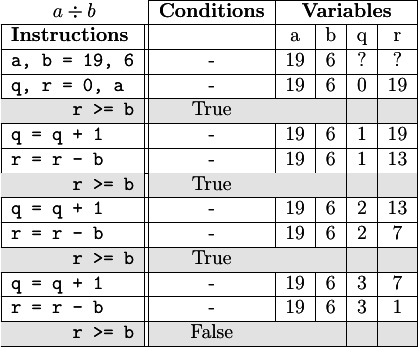
Pour déterminer les valeurs de variables après une séquence d’instructions, il faut suivre instruction après instruction (pas à pas) l’évolution des valeurs des variables concernées. Comme dans le cas de l'alternative, on insère une colonne « Conditions » avant celles des variables du problème.
Lorsqu'on rencontre une itération conditionnelle, on note la condition dans la
colonne des instructions
et on précise sa valeur (True ou False) dans la colonne « Conditions ».
Les lignes immédiatement suivantes du tableau correspondent aux instructions
du blocWhile si la condition est vraie, à celles qui suivent l'instruction
while condition : blocWhile si elle est fausse.
| Exemple 1 | Exemple 2 | ||||
|
|
Vérification
Lorsque le code est une donnée de l'énoncé, comme c'est le cas dans les 2 exemples précédents, une technique de vérification « évidente » consiste à le faire exécuter directement par l'interpréteur Python.
Pour suivre pas à pas l'exécution de la séquence d'affectations tel que le préconise la méthode de l'empathie numérique, nous reprenons le code proposé et, après chaque instruction, nous affichons les valeurs des conditions et des variables qui interviennent dans ce code.
L'exécution par Python des séquences précédentes donne bien les mêmes résultats que ceux que nous avons obtenus « à la main ».
Méthode de l'invariant
Un algorithme est un mécanisme qui fait passer un « système » d'un « état » initial (ou situation initiale, ou précondition) à un « état » final (ou situation finale, ou postcondition, ou but). Le couple (état initial, état final) est appelé spécification de l'algorithme. L'algorithmique vise ainsi à construire rationnellement des algorithmes à partir de leur spécification.
Cas introductif
On dispose d'une planche, d'un marteau et d'un clou (état initial) et on veut que le clou soit enfoncé dans la planche jusqu'à la tête (état final).
Le travail à réaliser consiste donc à planter légèrement le clou à la main de façon qu'il tienne seul, puis à taper sur la tête du clou avec le marteau tant que la tête ne touche pas la planche. Le nombre de coups nécessaire est à priori inconnu.
Le raisonnement qui permet de passer d'une compréhension intuitive d'un tel énoncé à l'algorithme n'est pas toujours facile à concevoir. Dans le cas d'une boucle on pourra systématiser la conception de l'algorithme autour de 4 étapes :
- Déterminer un invariant (ou hypothèse de récurrence) du système : « Le clou est planté dans la planche ».
- Déterminer la condition d'arrêt de la boucle : « La tête touche la planche ».
- Proposer une progression qui rapproche de la condition d'arrêt tout en conservant l'invariant : « Frapper un coup de marteau de façon à enfoncer un peu plus le clou ».
- L'initialisation de la boucle doit instaurer l'invariant : « Planter légèrement le clou à la main ».
Il faut noter que les étapes 1 et 2 définissent des situations
tandis que les étapes 3 et 4 concernent des actions.
Dans cette section, on notera les situations entre crochets ([]) pour les
distinguer des actions.
La recherche d'un invariant est l'étape clé autour de laquelle s'articule la conception des boucles. La conjonction de l'invariant et de la condition d'arrêt conduit logiquement au but recherché :
[« invariant » and « condition d'arrêt »]\(\Rightarrow\)[« but »]La condition d'arrêt seule n'implique pas le but : un clou posé sur la planche la pointe en l'air a bien la tête qui touche la planche, mais il n'est pas planté dans la planche.
La progression doit :
conserver l'invariant (pas de coup de marteau qui déplanterait le clou !). Plus précisément, la progression est un fragment d'algorithme défini par les situations initiale et finale suivantes :
- état initial :
[« invariant » and not « condition d'arrêt »] - état final :
[« invariant »]
Dans l'exemple du clou, étant donnée la précondition
[« le clou est planté dans la planche » and « la tête ne touche pas la planche »], et la postcondition[« le clou est enfoncé dans la planche »], une solution à la progression est« frapper un coup de marteau ».[« invariant » and not « condition d'arrêt »] « progression » [« invariant »]
- état initial :
faire effectivement progresser vers le but pour faire en sorte que la condition d'arrêt soit atteinte au bout d'un temps fini. Ici il est nécessaire de faire décroître la hauteur du clou au dessus de la planche.
L'initialisation doit instaurer l'invariant. Plus précisément, elle doit, partant de la précondition, atteindre l'invariant.
[« précondition »] « initialisation » [« invariant »]
Pour enfoncer un clou dans une planche, on exécutera ainsi l'algorithme suivant :
# état initial [« on dispose d'une planche d'un marteau, d'un clou »] # initialisation de la boucle « Planter légèrement le clou à la main » # invariant instauré par l'initialisation [« le clou est planté dans la planche »] # boucle « while not condition d'arrêt » while not [« la tête du clou touche la planche »] : # progression « frapper un coup de marteau sur la tête du clou » # invariant conservé par la progression [« le clou est planté dans la planche »] # état final [« le clou est enfoncé dans la planche »]
Cas général
D'une manière plus générale, les 4 étapes de construction d'une boucle sont les suivantes :
- Invariant : proposer une situation générale décrivant le problème posé (hypothèse de récurrence). C'est cette étape qui est la plus délicate car elle exige de faire preuve d'intuition.
- Condition d'arrêt : à partir de la situation générale imaginée en [1], on doit formuler la condition qui permet d'affirmer que l'algorithme a terminé son travail. La situation dans laquelle il se trouve alors est appelée situation finale. La condition d'arrêt fait sortir de la boucle.
- Progression : se « rapprocher » de la situation finale, tout en faisant le nécessaire pour conserver à chaque étape une situation générale analogue à celle retenue en [1]. La progression conserve l'invariant.
- Initialisation : initialiser les variables introduites dans l'invariant pour que celui-ci soit vérifié avant d'entrer dans la boucle. L'initialisation « instaure » l'invariant.
Une fois les 4 étapes précédentes menées à leur terme, l'algorithme recherché aura la structure finale suivante :
[« situation initiale »] « initialisation » [« invariant »] while not [« condition d'arrêt »] : « progression » [« invariant »] [« situation finale »]
Quand on sort de la boucle, la situation finale attendue est atteinte.
Dans la pratique, on ne garde que les instructions :
« initialisation » while [not « condition d'arrêt »] : « progression »
Un des problèmes, pour l'apprenti informaticien, est que la boucle finale ainsi obtenue ne fait pas apparaître explicitement l'invariant dans le code. L'invariant est une aide conceptuelle pour construire la boucle, mais pas pour l'exécuter.
Un invariant de boucle est une expression booléenne vérifiée avant l'entrée dans la boucle et qui reste vraie après chaque passage dans la boucle.
Cette façon de procéder permet de « prouver » la validité de l'algorithme
au fur et à mesure de son élaboration. En effet la situation générale
choisie en [1] est en fait l'invariant qui caractérise la boucle while.
Cette situation est satisfaite au départ grâce à l'initialisation de l'étape
[4]; elle reste vraie à chaque itération (étape [3]).
Ainsi lorsque la condition d'arrêt (étape [2])
est atteinte cette situation nous permet d'affirmer que le problème est résolu.
C'est également en analysant l'étape [3] qu'on peut prouver la terminaison
de l'algorithme : il faut vérifier à chaque passage dans la boucle
que la progression rapproche le système de la condition d'arrêt.
Applications
Reprenons les exemples de la division entière et du pgcd.
Division entière
- état initial : on dispose de 2 entiers \(a\) et \(b\).
- état final : les entiers \(q\) et \(r\) sont respectivement le quotient et le reste de la division entière \(a\div b\) (\(a = bq + r\) avec \(r < b\)).
Le quotient \(q\) s'obtient en soustrayant le diviseur \(b\) au dividande \(a\) autant de fois que possible jusqu'à ce qu'il ne reste plus qu'un reste \(r\) inférieur au diviseur \(b\).
| Méthode de l'invariant | Division entière |
| initialisation | x,y,q,r = a,b,0,a |
| invariant | à chaque étape : \(x = yq + r\) |
| condition d'arrêt | r < y |
| progression | q,r = q+1,r-y |
| boucle | x, y, q, r = a, b, 0, a
while not r < y :
q = q + 1
r = r - y
|
Plus grand commun diviseur
- état initial : on dispose de 2 entiers \(a\) et \(b\).
- état final : l'entier \(d\) est le pgcd de \(a\) et \(b\).
Le plus grand commun diviseur de 2 entiers \(a\) et \(b\) peut se calculer en appliquant la relation de récurrence \(\mathrm{pgcd}(a,b) = \mathrm{pgcd}(b,a\%b)\) jusqu'à ce que le reste (\(a\%b\)) soit nul :
\(\mathrm{pgcd}(a,b) = \mathrm{pgcd}(b,a\%b) = \mathrm{pgcd}(a\%b,b\%(a\%b)) = \cdots = \mathrm{pgcd}(d,0) = d\)
| Méthode de l'invariant | Plus grand commun diviseur |
| initialisation | x,y = a,b |
| invariant | à chaque étape : \(d = pgcd(x,y)\) |
| condition d'arrêt | y == 0 |
| progression | pgcd(x,y) = pgcd(y,x%y) : x,y = y,x%y |
| boucle | x, y = a, b
while not y == 0 :
x, y = y, x%y
|
Imbrications de boucles
De la même manière que l'on peut cascader des alternatives simples, on peut encapsuler une boucle dans une autre boucle.
Nous avons déjà affiché une table de multiplication dans un exemple précédent grâce à l'algorithme suivant :
# affichage d'une table
i = 0
while i < 10:
print i, '*', n, '=', i*n
i = i + 1
Nous voulons maintenant afficher les 9 premières tables de multiplication en réutilisant l'algorithme d'affichage d'une seule table. Il nous suffit pour cela de répéter 9 fois l'algorithme d'affichage d'une table en incrémentant le multiplicande $n$ à chaque itération :
# affichage des 9 tables
n = 1
while n <= 9:
# affichage d'une table
i = 0
while i < 10:
print i, '*', n, '=', i*n
i = i + 1
# passage à la table suivante
n = n + 1
On initialise n à 1 (on commence par la table de multiplication de 1),
puis on entre dans la boucle qui fera varier n de 1 à 9 (while n <= 9).
On exécute l'algorithme d'affichage d'une table et à la sortie de
cet algorithme, on n'oublie pas d'incrémenter n (n = n + 1) pour passer
à la table suivante. Et ainsi de suite jusqu'à la table de 9.
Quand n == 9, son incrémentation
lui affecte la valeur 10, ce qui rend fausse la condition de la boucle
(n <= 9) : on sort alors de la boucle extérieure.
Blocs d'instructions
Cet exemple d'instruction composée pose explicitement le problème de la
définition d'un bloc d'instructions : où commence et où termine un bloc
d'instructions ?
En effet, l'instruction n = n + 1 fait-elle partie du bloc de la boucle
intérieure (while i < 10:) ou du bloc de la boucle extérieure
(while n <= 9:) ?
Les instructions composées ont toujours la même structure :
une ligne d'en-tête terminée par un double point (:), suivie
d'une ou de plusieurs instructions indentées (décalées à droite)
sous cette ligne d'en-tête:
ligne d'en-tête :
première instruction du bloc
...
dernière instruction du bloc
C'est le cas des instructions conditionnelles et des instructions itératives :
| instruction | instruction conditionnelle | instruction itérative |
| ligne d'en-tête |
|
while condition : |
| exemple | if x < 0 :
x = x + 1
print x
elif x == 0 :
print x
else :
x = x - 1
print x
|
x = 10
while x > 0 :
x = x - 1
print x
|
S'il y a plusieurs instructions indentées sous la ligne d'en-tête, elles doivent l'être exactement au même niveau (décalage de 4 caractères espace, par exemple). Ces instructions indentées constituent ce qu'on appellera désormais un bloc d'instructions. Un bloc d'instructions est une suite d'instructions formant un ensemble logique (une macro-instruction), qui n'est exécuté que dans certaines conditions définies dans la ligne d'en-tête.
Dans l'exemple des tables de multiplication, les deux lignes
d'instructions indentées sous la ligne contenant l'instruction while i < 10 :
constituent un même bloc logique : ces deux lignes ne sont exécutées
que si la condition testée avec l'instruction while est vérifiée,
c'est-à-dire si le multiplicateur i est tel que 1 <= i < 10.
Grands classiques
Table de vérité
La table de vérité d'un circuit logique à \(n\) entrées
\((e_1,e_2,\ldots,e_n)\) et \(r\) sorties
\((s_1,s_2,\ldots,s_r)\) peut être calculée à l'aide
de \(n\) boucles imbriquées.
En effet, chaque entrée \(e_i\) peut prendre les valeurs 0 (False)
ou 1 (True), ce qui correspond à \(2^n\) combinaisons possibles entre
les \(n\) entrées.
Une première boucle va permettre d'explorer les 2 valeurs possibles
pour la première entrée \(e_1\). Puis pour chacune de ces 2 valeurs,
la deuxième boucle va permettre d'explorer les 2 valeurs possibles
pour la deuxième entrée \(e_2\). Et ainsi de suite jusqu'à la dernière
entrée \(e_n\), étape à laquelle on pourra effectivement calculer
les sorties \(s_j\) pour une combinaison donnée des valeurs
en entrée \((e_1,e_2,\ldots,e_n)\).
Pour chacune des boucles, on applique la méthode de l'invariant :
Méthode de l'invariant exploration des valeurs de l'entrée \(e_i\) initialisation e_i = 0invariant à chaque étape \(k\) : \(e_{i_k} = \{0,1\}[k]\) : \(e_{i_0} = \{0,1\}[0] = 0\) et \(e_{i_1} = \{0,1\}[1] = 1\) condition d'arrêt e_i > 1progression e_i = e_i + 1boucle
A titre d'exemples, considérons successivement le cas de la négation à une entrée et une sortie : \(s = \overline{e}\), de la disjonction à deux entrées et une sortie : \(s = e_1 + e_2\) et de la porte logique « non-et » à trois entrées et une sortie : \(s = \overline{e_1\cdot e_2\cdot e_3}\).
\(s = \overline{e}\)
1 entrée \(\Rightarrow 2^1 = 2\) combinaisons parcourues à l'aide d'une seule boucle :
python : iteration-negation.pyOutput\(s = e_1 + e_2\)
2 entrées \(\Rightarrow 2^2 = 4\) combinaisons parcourues à l'aide de 2 boucles imbriquées :
python : iteration-disjonction.pyOutput\(s = \overline{e_1\cdot e_2\cdot e_3}\)
3 entrées \(\Rightarrow 2^3 = 8\) combinaisons parcourues à l'aide de 3 boucles imbriquées :
python : iteration-non-et-3.pyOutput
Motifs en quinconce
Un motif en quinconce est formé de \(n\times m\) figures géométriques
disposées en quinconce comme l'indique la figure ci-dessous où le motif est un
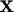incliné à 30° (
) :
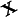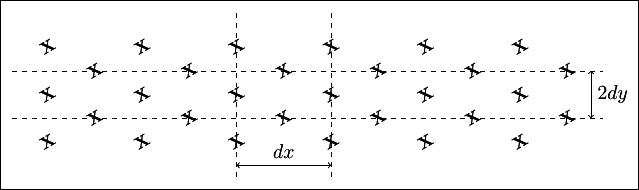
Pour dessiner un tel motif, on va dessiner les lignes de motifs les unes après les autres (de la ligne numéro 0 à la ligne de numéro \(m-1\)) en décalant l'origine de la ligne de \((dx/2)\) une ligne sur deux.
Méthode de l'invariant dessiner les lignes initialisation ligne, xl, yl = 0, x0, y0invariant à chaque étape, (xl,yl)représente l'origine de la lignecondition d'arrêt ligne == mprogression passer à la ligne suivante en recalculant la nouvelle origine boucle
Pour dessiner une ligne de motifs, on se déplace de colonne en colonne (de la colonne numéro 0 à la colonne de numéro \(n-1\)) pour dessiner le motif au niveau de chaque colonne.
Méthode de l'invariant dessiner les colonnes initialisation colonne, xc, yc = 0, xl, ylinvariant à chaque étape, (xc,yc)représente l'origine de la colonnecondition d'arrêt colonne == nprogression passer à la colonne suivante en recalculant la nouvelle origine boucle
Il ne reste plus qu'à dessiner le motif en (xc,yc).
On déplace la tortue t jusqu'en (xc,yc) sans dessiner
puis on trace le motif:
t.up()
t.goto(xc,yc)
t.down()
A titre d'exemples, considérons successivement le stère de bois et le nid d'abeille.
Stère de bois
Ici, la figure géométrique est un cercle
que l'on dessine simplement avec la méthode circlede la tortue Logo:t.circle(rayon)
python : iteration-stere-bois.pyOutputNid d'abeilles
Ici la figure géométrique est un hexagone régulier
que l'on dessine lui-même avec une boucle de « suivi de trajectoire »:c = 0 while c < 6 : t.forward(d) t.left(360./6)
python : iteration-nid-abeilles.pyOutput