tester si x est de type bool ou si x est membre de la liste [0,1]:
```
ok = isBoolean(x)
```
tester si x est de type int ou de type float:
```
ok = isNumber(x)
```
tester si t est de type str, tuple ou list:
```
ok = isSequence(x)
```
tester si les éléments de la séquence t sont de même type:
```
ok = isHomogeneousSequence(t)
```
tester si t est une matrice \(n \times n\):
```
ok = isMatrix(t,n,m)
```

Définir les 5 fonctions précédentes : isBoolean, isNumber, isSequence, isHomogeneousSequence et isMatrix.
On vérifiera un à un les différents tests.

Votre réponse :

AAV4_APP: Résultat

Utiliser l'interpréteur Python ci-dessous pour programmer les fonctions demandées.

python : essai.py

Output

Interpréteur

Menu	Action
	Ré-initialiser les sorties
	Faire apparaître le menu d'aide
	Interpréter le programme

Editeur

Menu	Raccouci	Action
	`Ctrl+N`	Initialiser l'éditeur
	`Ctrl+O`	Charger le contenu d'un fichier dans l'éditeur
	`Ctrl+S`	Sauvegarder le contenu de l'éditeur dans un fichier
	`Ctrl+P`	Imprimer le contenu de l'éditeur
	`Ctrl+Z`	Annuler la dernière modification
	`Maj+Ctrl+Z`	Rétablir la modification précedente
	`Ctrl+F`	Chercher une expression dans l'éditeur
	`Maj+Ctrl+F`	Chercher et remplacer une expression par une autre
	`F10`	Ouvrir une documentation du langage

Raccourci	Action
`F1`	Afficher cette aide
`Tab`	Indenter la sélection
`Maj+Tab`	Désindenter la sélection
`Ctrl+A`	Sélectionner le contenu de l'éditeur
`Ctrl+C`	Copier la sélection dans le presse-papier
`Ctrl+V`	Remplacer la sélection par le contenu du presse-papier
`Ctrl+X`	Supprimer la sélection et la copier dans le presse-papier
`Maj+Ctrl+R`	Chercher et remplacer une expression par une autre dans tout l'éditeur

AAV4_APP: Vérification

Appliquer cette technique au résultat proposé.

Si cette technique nécessite d'être implémentée en Python, le faire dans l'interpréteur Python ci-dessus (cf. Résultat), sinon développer la technique de vérification dans l'éditeur de texte ci-dessous.

Zone de saisie de texte

Clavier	Action
`F1`	Afficher une aide technique
`F2`	Afficher une aide pédagogique
`Ctrl-A`	Tout sélectionner
`Ctrl-C`	Copier la sélection dans le presse-papier
`Ctrl-V`	Copier le presse-papier dans la sélection
`Ctrl-X`	Couper la sélection et la copier dans le presse-papier
`Ctrl-Z`	Annuler la modification
`Maj-Ctrl-Z`	Rétablir la modification

Menu	Action
	Ré-initialiser les sorties
	Faire apparaître le menu d'aide
	Valider la zone de saisie
	Initialiser la zone de saisie
	Charger le contenu d'un fichier dans la zone de saisie
	Sauvegarder le contenu de la zone de saisie dans un fichier
	Imprimer le contenu de la zone de saisie

Une solution possible :

AAV4_APP: Répondre explicitement à la question posée

Les fonctions demandées sont définies ci-dessous :

python : appels-type-types.py

# -*- coding: utf-8 -*-

# définitions
def isBoolean(x) :
    u"""
    ok = isBoolean(x)
    True si x est de type bool ou x dans [0,1],
    False sinon.
    """
    return type(x) is bool or x in [0,1]

def isNumber(x) :
    """
    ok = isNumber(x)
    True si x est de type int ou de type float,
    False sinon.
    """
    return type(x) is int or type(x) is float

def isSequence(t) :
    u"""
    ok = isSequence(t)
    True si t est de type str ou de type tuple ou de type list,
    False sinon.
    """
    return type(t) is str or type(t) is tuple or type(t) is list

def isHomogeneousSequence(t) :
    u"""
    ok = isHomogeneousSequence(t)
    True si les éléments de la séquence t sont de même type,
    False sinon.
    """

if type(t) is str :
        ok = True
    elif type(t) is tuple or type(t) is list :
        ok = True
        i = 1
        while i < len(t) and ok :
            if type(t[i]) != type(t[0]) :
                ok = False
            i = i + 1
    else :
        ok = False
    return ok

def isMatrix(t,n,m) :
    u"""
    ok = isMatrix(t,n,m)
    True si t est une matrice homogène de n lignes et m colonnes,
    False sinon.
    """
    assert type(t) is list
    assert isHomogeneousSequence(t)
    assert type(n) is int and n > 0
    assert type(m) is int and m > 0
    if n != len(t) :
        ok = False
    elif type(t[0]) is list :
        if m != len(t[0]) :
            ok = False
        else :
            i = 1
            ok = True
            while i < len(t) and ok :
                if m != len(t[i]) :
                    ok = False
                else :
                    i = i + 1
    else :
        ok = False

return ok

# vérification
if __name__ == "__main__" :
    # vérification 1
    booleans = [True,False,0,1,2,'True','False']
    for b in booleans :
        print 'v1 :',b,isBoolean(b)
    print

# vérification 2
    import math
    numbers = [True,False,0,1,2,'12','3,14',45.1,2.e-6,math.pi,math.sin(math.pi/2)]
    for n in numbers :
        print 'v2 :',n,isNumber(n)
    print

# vérification 3
    sequences = ["",(),[],"hello",(1),(1,),[[[]]],([1,2,3])]
    for s in sequences :
        print 'v3 :',s,isSequence(s)
    print

# vérification 4
    sequences = ["",(),[],"hello",(1),(1,),[[[]]],([1,2,3])]
    sequences += [[[1,(1,2)],["e",[1,"r"]]],[1,2.2,'e'],([1,2],['e','r'],['e',3])]
    for s in sequences :
        print 'v4 :',s,isHomogeneousSequence(s)
    print

# vérification 5
    n, m = 3, 2
    obj = [[1,2,3], [[1,2,3],[3,2,1]], [[2,1],[3,2],[4,2]], [[1,[2]],[[2],1],[[1],[2]]] ]
    for t in obj :
        print 'v5 :',t,n,m,isMatrix(t,n,m)

Output

Interpréteur

Menu	Action
	Ré-initialiser les sorties
	Faire apparaître le menu d'aide
	Interpréter le programme

Editeur

Menu	Raccouci	Action
	`Ctrl+N`	Initialiser l'éditeur
	`Ctrl+O`	Charger le contenu d'un fichier dans l'éditeur
	`Ctrl+S`	Sauvegarder le contenu de l'éditeur dans un fichier
	`Ctrl+P`	Imprimer le contenu de l'éditeur
	`Ctrl+Z`	Annuler la dernière modification
	`Maj+Ctrl+Z`	Rétablir la modification précedente
	`Ctrl+F`	Chercher une expression dans l'éditeur
	`Maj+Ctrl+F`	Chercher et remplacer une expression par une autre
	`F10`	Ouvrir une documentation du langage

Raccourci	Action
`F1`	Afficher cette aide
`Tab`	Indenter la sélection
`Maj+Tab`	Désindenter la sélection
`Ctrl+A`	Sélectionner le contenu de l'éditeur
`Ctrl+C`	Copier la sélection dans le presse-papier
`Ctrl+V`	Remplacer la sélection par le contenu du presse-papier
`Ctrl+X`	Supprimer la sélection et la copier dans le presse-papier
`Maj+Ctrl+R`	Chercher et remplacer une expression par une autre dans tout l'éditeur

AAV4_APP: Choisir et appliquer une technique de vérification

Des vérifications par jeux de tests sont proposées dans l'énoncé:

# vérification 1
booleans = [True,False,0,1,2,'True','False']
for b in booleans :
    print 'v1 :',b,isBoolean(b)
print

# vérification 2
import math
numbers = [True,False,0,1,2,'12','3,14',45.1,2.e-6,math.pi,math.sin(math.pi/2)]
for n in numbers :
    print 'v2 :',n,isNumber(n)
print

# vérification 3
sequences = ["",(),[],"hello",(1),(1,),[[[]]],([1,2,3])]
for s in sequences :
    print 'v3 :',s,isSequence(s)
print

# vérification 4
sequences = ["",(),[],"hello",(1),(1,),[[[]]],([1,2,3])]
sequences += [[[1,(1,2)],["e",[1,"r"]]],[1,2.2,'e'],([1,2],['e','r'],['e',3])]
for s in sequences :
    print 'v4 :',s,isHomogeneousSequence(s)
print

# vérification 5
n, m = 3, 2
obj = [[1,2,3], [[1,2,3],[3,2,1]], [[2,1],[3,2],[4,2]], [[1,[2]],[[2],1],[[1],[2]]] ]
for t in obj :
    print 'v5 :',t,n,m,isMatrix(t,n,m)

Opérateurs booléens dérivés

Définir la fonction xor(a,b) qui correspond à l'opérateur logique « ou exclusif ».
En utilisant la fonction précédente, définir la fonction circuit(a,b,c) qui retourne les sorties s et t du circuit logique ci-dessous.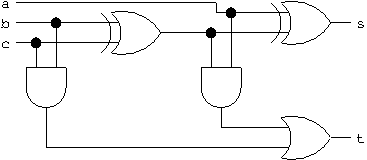
En utilisant la fonction précédente, définir une fonction table() qui affiche la table de vérité du circuit précédent. Les entrées-sorties seront représentées par des 0 et des 1 (non par False ou True).

opérateurs booléens

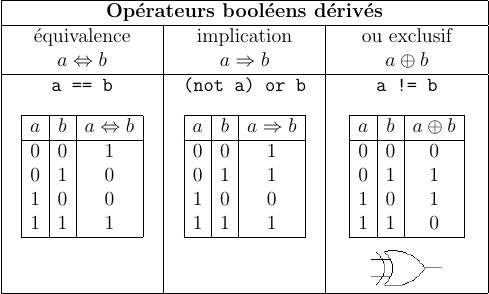
Votre réponse :

AAV4_APP: Résultat

Utiliser l'interpréteur Python ci-dessous pour programmer les fonctions demandées.

python : essai.py

Output

Interpréteur

Menu	Action
	Ré-initialiser les sorties
	Faire apparaître le menu d'aide
	Interpréter le programme

Editeur

Menu	Raccouci	Action
	`Ctrl+N`	Initialiser l'éditeur
	`Ctrl+O`	Charger le contenu d'un fichier dans l'éditeur
	`Ctrl+S`	Sauvegarder le contenu de l'éditeur dans un fichier
	`Ctrl+P`	Imprimer le contenu de l'éditeur
	`Ctrl+Z`	Annuler la dernière modification
	`Maj+Ctrl+Z`	Rétablir la modification précedente
	`Ctrl+F`	Chercher une expression dans l'éditeur
	`Maj+Ctrl+F`	Chercher et remplacer une expression par une autre
	`F10`	Ouvrir une documentation du langage

Raccourci	Action
`F1`	Afficher cette aide
`Tab`	Indenter la sélection
`Maj+Tab`	Désindenter la sélection
`Ctrl+A`	Sélectionner le contenu de l'éditeur
`Ctrl+C`	Copier la sélection dans le presse-papier
`Ctrl+V`	Remplacer la sélection par le contenu du presse-papier
`Ctrl+X`	Supprimer la sélection et la copier dans le presse-papier
`Maj+Ctrl+R`	Chercher et remplacer une expression par une autre dans tout l'éditeur

AAV4_APP: Vérification

Appliquer cette technique au résultat proposé.

Zone de saisie de texte

Clavier	Action
`F1`	Afficher une aide technique
`F2`	Afficher une aide pédagogique
`Ctrl-A`	Tout sélectionner
`Ctrl-C`	Copier la sélection dans le presse-papier
`Ctrl-V`	Copier le presse-papier dans la sélection
`Ctrl-X`	Couper la sélection et la copier dans le presse-papier
`Ctrl-Z`	Annuler la modification
`Maj-Ctrl-Z`	Rétablir la modification

Menu	Action
	Ré-initialiser les sorties
	Faire apparaître le menu d'aide
	Valider la zone de saisie
	Initialiser la zone de saisie
	Charger le contenu d'un fichier dans la zone de saisie
	Sauvegarder le contenu de la zone de saisie dans un fichier
	Imprimer le contenu de la zone de saisie

Une solution possible :

AAV4_APP: Répondre explicitement à la question posée

Les fonctions demandées sont définies ci-dessous :

python : appels-type-boolean.py

# -*- coding: utf-8 -*-

# définitions
def xor(a,b) :
    u"""
    x = xor(a,b)
    résultat de l'opération logique « ou exclusif » entre les booléens a et b.
    """
    assert type(a) is bool or a in [0,1]
    assert type(b) is bool or b in [0,1]
    return a != b

def circuit(a,b,c) :
    u"""
    s,t = circuit(a,b,c)
    sorties du circuit logique donnée en figure dans l'énoncé.
    """
    assert type(a) is bool or a in [0,1]
    assert type(b) is bool or b in [0,1]
    assert type(c) is bool or c in [0,1]
    u = xor(b,c)
    s = xor(a,u)
    t = (b and c) or (a and u)
    return s,t

def table() :
    u"""
    affiche la table de vérité du circuit donnée en figure dans l'énoncé
    les entrées et les sorties sont affichées sous forme d'entiers 0 et 1
    et non sous forme de booléens True et False.
    """
    for a in [0,1] :
        for b in [0,1] :
            for c in [0,1] :
                s,t = circuit(a,b,c)
                print a,b,c,int(s),int(t)
    return

# vérification
if __name__ == "__main__" :
    table()

Output

Interpréteur

Menu	Action
	Ré-initialiser les sorties
	Faire apparaître le menu d'aide
	Interpréter le programme

Editeur

Menu	Raccouci	Action
	`Ctrl+N`	Initialiser l'éditeur
	`Ctrl+O`	Charger le contenu d'un fichier dans l'éditeur
	`Ctrl+S`	Sauvegarder le contenu de l'éditeur dans un fichier
	`Ctrl+P`	Imprimer le contenu de l'éditeur
	`Ctrl+Z`	Annuler la dernière modification
	`Maj+Ctrl+Z`	Rétablir la modification précedente
	`Ctrl+F`	Chercher une expression dans l'éditeur
	`Maj+Ctrl+F`	Chercher et remplacer une expression par une autre
	`F10`	Ouvrir une documentation du langage

Raccourci	Action
`F1`	Afficher cette aide
`Tab`	Indenter la sélection
`Maj+Tab`	Désindenter la sélection
`Ctrl+A`	Sélectionner le contenu de l'éditeur
`Ctrl+C`	Copier la sélection dans le presse-papier
`Ctrl+V`	Remplacer la sélection par le contenu du presse-papier
`Ctrl+X`	Supprimer la sélection et la copier dans le presse-papier
`Maj+Ctrl+R`	Chercher et remplacer une expression par une autre dans tout l'éditeur

AAV4_APP: Choisir et appliquer une technique de vérification

Ce circuit correspond à un additionneur à 3 entrées \(a\), \(b\), \(c\) et 2 sorties \(s\), \(t\) tel que le nombre binaire \((ts)_2\) est la somme binaire \((a+b+c)_2\) des 3 entrées :

Par un simple calcul « à la main », on trouve que cet additionneur « 3 bits » a pour table de vérité :

\(\displaystyle \begin{array}{ccc|cc} a & b & c & s & t \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 1 & 0 \\ 0 & 1 & 0 & 1 & 0 \\ 0 & 1 & 1 & 0 & 1 \\ 1 & 0 & 0 & 1 & 0 \\ 1 & 0 & 1 & 0 & 1 \\ 1 & 1 & 0 & 0 & 1 \\ 1 & 1 & 1 & 1 & 1 \end{array}\)

Le programme Python obtient bien la même table de vérité.

Codage/décodage d'un nombre

Définir la fonction codage(n,b,k) qui code en base \(b\) un entier \(n\) sur \(k\) chiffres.
Définir la fonction decodage(c,b) qui décode en base 10 le code \(c\) d'un entier codé en base \(b\).
Vérifier que :
1. decodage(codage(n,b,k),b) == n
2. codage(decodage(c,b),b,len(c)) == c

Votre réponse :

AAV4_APP: Résultat

Utiliser l'interpréteur Python ci-dessous pour programmer les fonctions demandées.

python : essai.py

Output

Interpréteur

Menu	Action
	Ré-initialiser les sorties
	Faire apparaître le menu d'aide
	Interpréter le programme

Editeur

Menu	Raccouci	Action
	`Ctrl+N`	Initialiser l'éditeur
	`Ctrl+O`	Charger le contenu d'un fichier dans l'éditeur
	`Ctrl+S`	Sauvegarder le contenu de l'éditeur dans un fichier
	`Ctrl+P`	Imprimer le contenu de l'éditeur
	`Ctrl+Z`	Annuler la dernière modification
	`Maj+Ctrl+Z`	Rétablir la modification précedente
	`Ctrl+F`	Chercher une expression dans l'éditeur
	`Maj+Ctrl+F`	Chercher et remplacer une expression par une autre
	`F10`	Ouvrir une documentation du langage

Raccourci	Action
`F1`	Afficher cette aide
`Tab`	Indenter la sélection
`Maj+Tab`	Désindenter la sélection
`Ctrl+A`	Sélectionner le contenu de l'éditeur
`Ctrl+C`	Copier la sélection dans le presse-papier
`Ctrl+V`	Remplacer la sélection par le contenu du presse-papier
`Ctrl+X`	Supprimer la sélection et la copier dans le presse-papier
`Maj+Ctrl+R`	Chercher et remplacer une expression par une autre dans tout l'éditeur

AAV4_APP: Vérification

Appliquer cette technique au résultat proposé.

Zone de saisie de texte

Clavier	Action
`F1`	Afficher une aide technique
`F2`	Afficher une aide pédagogique
`Ctrl-A`	Tout sélectionner
`Ctrl-C`	Copier la sélection dans le presse-papier
`Ctrl-V`	Copier le presse-papier dans la sélection
`Ctrl-X`	Couper la sélection et la copier dans le presse-papier
`Ctrl-Z`	Annuler la modification
`Maj-Ctrl-Z`	Rétablir la modification

Menu	Action
	Ré-initialiser les sorties
	Faire apparaître le menu d'aide
	Valider la zone de saisie
	Initialiser la zone de saisie
	Charger le contenu d'un fichier dans la zone de saisie
	Sauvegarder le contenu de la zone de saisie dans un fichier
	Imprimer le contenu de la zone de saisie

Une solution possible :

AAV4_APP: Répondre explicitement à la question posée

Les fonctions demandées sont définies ci-dessous :

python : appels-type-number-1.py

# -*- coding: utf-8 -*-

# définitions
def codage(n,b,k) :
    u"""
    code = codage(n,b,k)
    liste des chiffres de la base b qui représente l'entier décimal n
    codé sur k chiffres.
    """
    assert type(n) is int and n >= 0
    assert type(b) is int and b > 1
    assert type(k) is int and k > 0
    assert n < b**k
    i, code = 0, []
    while i < k :
        code.append(0)
        i = i + 1

q, r = n, n%b
    i, code[k-1] = 0, r
    while q != 0 and i < k-1 :
        q = q/b
        r = q%b
        i = i + 1
        code[k-1-i] = r
    return code

def decodage(c,b) :
    u"""
    n = decodage(c,b)
    entier décimal qui représente la liste c de chiffre en base b.
    """
    assert type(c) is list and len(c) > 0
    assert type(b) is int and b > 1
    i, n = 0, c[len(c)-1]
    while i < len(c)-1 :
        i = i + 1
        n = n + c[len(c)-1-i]*b**i
    return n

# vérification
if __name__ == "__main__" :
    import random, sys
    n = random.randint(0,200)
    b = random.randint(2,16)
    k = random.randint(1,16)
    while b**k <= n : k = random.randint(1,16)
    code = codage(n,b,k)
    verif1 = (n == decodage(code,b))
    print 'v1 :',n,b,k,code,verif1

b = random.randint(2,16)
    k = random.randint(1,10)
    while b**k >= sys.maxsize : k = random.randint(1,10)
    i, code = 0, []
    while i < k :
        code.append(random.randint(0,b-1))
        i = i + 1
    n = decodage(code,b)
    verif2 = (code == codage(n,b,len(code)))
    print 'v2 :',n,b,k,code,verif2

Output

Interpréteur

Menu	Action
	Ré-initialiser les sorties
	Faire apparaître le menu d'aide
	Interpréter le programme

Editeur

Menu	Raccouci	Action
	`Ctrl+N`	Initialiser l'éditeur
	`Ctrl+O`	Charger le contenu d'un fichier dans l'éditeur
	`Ctrl+S`	Sauvegarder le contenu de l'éditeur dans un fichier
	`Ctrl+P`	Imprimer le contenu de l'éditeur
	`Ctrl+Z`	Annuler la dernière modification
	`Maj+Ctrl+Z`	Rétablir la modification précedente
	`Ctrl+F`	Chercher une expression dans l'éditeur
	`Maj+Ctrl+F`	Chercher et remplacer une expression par une autre
	`F10`	Ouvrir une documentation du langage

Raccourci	Action
`F1`	Afficher cette aide
`Tab`	Indenter la sélection
`Maj+Tab`	Désindenter la sélection
`Ctrl+A`	Sélectionner le contenu de l'éditeur
`Ctrl+C`	Copier la sélection dans le presse-papier
`Ctrl+V`	Remplacer la sélection par le contenu du presse-papier
`Ctrl+X`	Supprimer la sélection et la copier dans le presse-papier
`Maj+Ctrl+R`	Chercher et remplacer une expression par une autre dans tout l'éditeur

AAV4_APP: Choisir et appliquer une technique de vérification

Des vérifications par jeux de tests sont proposées dans l'énoncé:

import random, sys

# vérification 1
n = random.randint(0,200)
b = random.randint(2,16)
k = random.randint(1,16)
while b**k <= n : k = random.randint(1,16)
code = codage(n,b,k)
verif1 = (n == decodage(code,b))
print 'v1 :',n,b,k,code,verif1

# vérification 2
b = random.randint(2,16)
k = random.randint(1,10)
while b**k >= sys.maxsize : k = random.randint(1,10)
i, code = 0, []
while i < k :
    code.append(random.randint(0,b-1))
    i = i + 1
n = decodage(code,b)
verif2 = (code == codage(n,b,len(code)))
print 'v2 :',n,b,k,code,verif2

Palindrome

Définir la fonction inverse(s,d,f) qui retourne une copie de la chaîne de caractères s dans laquelle la sous-chaîne entre les rangs d inclus et f exclu a été inversée.

Exemples :
- inverse("bonjour",2,5) \(\rightarrow\) "boojnur"
- inverse("bonjour",0,4) \(\rightarrow\) "jnobour"
En utilisant la fonction précédente, définir la fonction palindrome(s) qui teste si la chaîne de caractères s est un palindrome.

Votre réponse :

AAV4_APP: Résultat

Utiliser l'interpréteur Python ci-dessous pour programmer les fonctions demandées.

python : essai.py

Output

Interpréteur

Menu	Action
	Ré-initialiser les sorties
	Faire apparaître le menu d'aide
	Interpréter le programme

Editeur

Menu	Raccouci	Action
	`Ctrl+N`	Initialiser l'éditeur
	`Ctrl+O`	Charger le contenu d'un fichier dans l'éditeur
	`Ctrl+S`	Sauvegarder le contenu de l'éditeur dans un fichier
	`Ctrl+P`	Imprimer le contenu de l'éditeur
	`Ctrl+Z`	Annuler la dernière modification
	`Maj+Ctrl+Z`	Rétablir la modification précedente
	`Ctrl+F`	Chercher une expression dans l'éditeur
	`Maj+Ctrl+F`	Chercher et remplacer une expression par une autre
	`F10`	Ouvrir une documentation du langage

Raccourci	Action
`F1`	Afficher cette aide
`Tab`	Indenter la sélection
`Maj+Tab`	Désindenter la sélection
`Ctrl+A`	Sélectionner le contenu de l'éditeur
`Ctrl+C`	Copier la sélection dans le presse-papier
`Ctrl+V`	Remplacer la sélection par le contenu du presse-papier
`Ctrl+X`	Supprimer la sélection et la copier dans le presse-papier
`Maj+Ctrl+R`	Chercher et remplacer une expression par une autre dans tout l'éditeur

AAV4_APP: Vérification

Appliquer cette technique au résultat proposé.

Zone de saisie de texte

Clavier	Action
`F1`	Afficher une aide technique
`F2`	Afficher une aide pédagogique
`Ctrl-A`	Tout sélectionner
`Ctrl-C`	Copier la sélection dans le presse-papier
`Ctrl-V`	Copier le presse-papier dans la sélection
`Ctrl-X`	Couper la sélection et la copier dans le presse-papier
`Ctrl-Z`	Annuler la modification
`Maj-Ctrl-Z`	Rétablir la modification

Menu	Action
	Ré-initialiser les sorties
	Faire apparaître le menu d'aide
	Valider la zone de saisie
	Initialiser la zone de saisie
	Charger le contenu d'un fichier dans la zone de saisie
	Sauvegarder le contenu de la zone de saisie dans un fichier
	Imprimer le contenu de la zone de saisie

Une solution possible :

AAV4_APP: Répondre explicitement à la question posée

Les fonctions demandées sont définies ci-dessous :

python : appels-type-string.py

Output

Interpréteur

Menu	Action
	Ré-initialiser les sorties
	Faire apparaître le menu d'aide
	Interpréter le programme

Editeur

Menu	Raccouci	Action
	`Ctrl+N`	Initialiser l'éditeur
	`Ctrl+O`	Charger le contenu d'un fichier dans l'éditeur
	`Ctrl+S`	Sauvegarder le contenu de l'éditeur dans un fichier
	`Ctrl+P`	Imprimer le contenu de l'éditeur
	`Ctrl+Z`	Annuler la dernière modification
	`Maj+Ctrl+Z`	Rétablir la modification précedente
	`Ctrl+F`	Chercher une expression dans l'éditeur
	`Maj+Ctrl+F`	Chercher et remplacer une expression par une autre
	`F10`	Ouvrir une documentation du langage

Raccourci	Action
`F1`	Afficher cette aide
`Tab`	Indenter la sélection
`Maj+Tab`	Désindenter la sélection
`Ctrl+A`	Sélectionner le contenu de l'éditeur
`Ctrl+C`	Copier la sélection dans le presse-papier
`Ctrl+V`	Remplacer la sélection par le contenu du presse-papier
`Ctrl+X`	Supprimer la sélection et la copier dans le presse-papier
`Maj+Ctrl+R`	Chercher et remplacer une expression par une autre dans tout l'éditeur

AAV4_APP: Choisir et appliquer une technique de vérification

Des vérifications par jeux de tests sont proposées dans l'énoncé:
```
mots = ["oui","non","kayak","bonjour","laval","mon nom"]
for m in mots :
    print m,palindrome(m)
```

Piles

Dans de nombreux cas, les seules opérations à effectuer sur les listes sont des insertions et des suppressions aux extrémités de la liste. C'est le cas en particulier des piles (stack).

Exemple : pile d'assiettes

Dans une pile d'assiettes, on ajoute des assiettes au sommet de la pile, et on les récupère dans l'ordre inverse, en commençant par la dernière ajoutée.

Définition : pile

Une pile est une séquence dans laquelle on ne peut ajouter et ne supprimer un élément qu'à une seule extrémité : le « sommet » de la pile.

Dans le cas des piles, on ajoute (on empile) et on supprime (on dépile) à une seule extrémité. Une pile est ainsi basée sur le principe « dernier arrivé, premier sorti » (structure Lifo : Last In, First Out) : le dernier élément ajouté au sommet de la pile sera le premier à être récupéré.

Les principales opérations nécessaires pour une pile sont ainsi :

créer une pile vide p:
p = Stack()
tester si la pile p est vide:
ok = empty(p)
accéder au sommet x de la pile p:
x = top(p)
empiler un élément x au sommet de la pile p:
push(p,x)
dépiler l'élément x qui se trouve au sommet de la pile p:
x = pop(p)
sérialiser une pile p sous la forme d'une chaîne de caractères s ("[e1,e2...]"):
s = toString(p)

Définir les 6 fonctions précédentes concernant les piles : Stack, empty, top, push, pop et toString. Une pile sera implémentée par une liste.
Vérifier que :
1. empty(Stack()) == True
2. top(p) == pop(p) et que pop(p) != top(p);
3. x == pop(p) juste après avoir empiler x sur la pile p (push(p,x));
4. p est inchangée après l'opération push(p,pop(p)).

Votre réponse :

AAV4_APP: Résultat

Utiliser l'interpréteur Python ci-dessous pour programmer les fonctions demandées.

python : essai.py

Output

Interpréteur

Menu	Action
	Ré-initialiser les sorties
	Faire apparaître le menu d'aide
	Interpréter le programme

Editeur

Menu	Raccouci	Action
	`Ctrl+N`	Initialiser l'éditeur
	`Ctrl+O`	Charger le contenu d'un fichier dans l'éditeur
	`Ctrl+S`	Sauvegarder le contenu de l'éditeur dans un fichier
	`Ctrl+P`	Imprimer le contenu de l'éditeur
	`Ctrl+Z`	Annuler la dernière modification
	`Maj+Ctrl+Z`	Rétablir la modification précedente
	`Ctrl+F`	Chercher une expression dans l'éditeur
	`Maj+Ctrl+F`	Chercher et remplacer une expression par une autre
	`F10`	Ouvrir une documentation du langage

Raccourci	Action
`F1`	Afficher cette aide
`Tab`	Indenter la sélection
`Maj+Tab`	Désindenter la sélection
`Ctrl+A`	Sélectionner le contenu de l'éditeur
`Ctrl+C`	Copier la sélection dans le presse-papier
`Ctrl+V`	Remplacer la sélection par le contenu du presse-papier
`Ctrl+X`	Supprimer la sélection et la copier dans le presse-papier
`Maj+Ctrl+R`	Chercher et remplacer une expression par une autre dans tout l'éditeur

AAV4_APP: Vérification

Appliquer cette technique au résultat proposé.

Zone de saisie de texte

Clavier	Action
`F1`	Afficher une aide technique
`F2`	Afficher une aide pédagogique
`Ctrl-A`	Tout sélectionner
`Ctrl-C`	Copier la sélection dans le presse-papier
`Ctrl-V`	Copier le presse-papier dans la sélection
`Ctrl-X`	Couper la sélection et la copier dans le presse-papier
`Ctrl-Z`	Annuler la modification
`Maj-Ctrl-Z`	Rétablir la modification

Menu	Action
	Ré-initialiser les sorties
	Faire apparaître le menu d'aide
	Valider la zone de saisie
	Initialiser la zone de saisie
	Charger le contenu d'un fichier dans la zone de saisie
	Sauvegarder le contenu de la zone de saisie dans un fichier
	Imprimer le contenu de la zone de saisie

Une solution possible :

AAV4_APP: Répondre explicitement à la question posée

Les fonctions demandées sont définies ci-dessous :

python : appels-type-list-1.py

# -*- coding: utf-8 -*-

# définitions
def Stack() :
    u'''
    p = Stack()
    crée une pile p vide
    '''
    return []

def empty(p) :
    u'''
    ok = empty(p)
    True si la pile p est vide, False sinon.
    '''
    assert type(p) is list
    return len(p) == 0

def top(p) :
    u'''
    x = top(p)
    sommet de la pile p non vide.
    '''
    assert type(p) is list
    assert not empty(p)
    return p[len(p)-1]

def push(p,x) :
    u'''
    push(p,x)
    empile x sur le sommet de la pile p.
    '''
    assert type(p) is list
    p.append(x)
    return

def pop(p) :
    u'''
    x = pop(p)
    dépile par le sommet la pile p non vide.
    '''
    assert type(p) is list
    assert not empty(p)
    x = top(p)
    del p[len(p)-1]
    return x

def toString(p) :
    u'''
    s = toString(p)
    chaîne représentant la file p
    '''
    assert type(p) is list
    return str(p)

# vérifications
if __name__ == "__main__" :
    # initialisation
    p = Stack()

# vérification 1
    verif1 = empty(p)
    print u'vérification 1 :',toString(p),verif1

for i in range(9) :
        push(p,i)
        print i, toString(p)

# vérification 2
    verif2 = top(p) == pop(p)
    print u'vérification 2 :',toString(p),verif2

# vérification 3
    verif3 = pop(p) != top(p)
    print u'vérification 3 :',toString(p),verif3

# vérification 4
    x = 9
    push(p,x)
    verif4 = x == pop(p)
    print u'vérification 4 :',toString(p),verif4

# vérification 5
    p1 = toString(p)
    push(p,pop(p))
    p2 = toString(p)
    verif5 = p1 == p2
    print u'vérification 5 :',toString(p),verif5

while not empty(p) :
        print pop(p),toString(p)

Output

Interpréteur

Menu	Action
	Ré-initialiser les sorties
	Faire apparaître le menu d'aide
	Interpréter le programme

Editeur

Menu	Raccouci	Action
	`Ctrl+N`	Initialiser l'éditeur
	`Ctrl+O`	Charger le contenu d'un fichier dans l'éditeur
	`Ctrl+S`	Sauvegarder le contenu de l'éditeur dans un fichier
	`Ctrl+P`	Imprimer le contenu de l'éditeur
	`Ctrl+Z`	Annuler la dernière modification
	`Maj+Ctrl+Z`	Rétablir la modification précedente
	`Ctrl+F`	Chercher une expression dans l'éditeur
	`Maj+Ctrl+F`	Chercher et remplacer une expression par une autre
	`F10`	Ouvrir une documentation du langage

Raccourci	Action
`F1`	Afficher cette aide
`Tab`	Indenter la sélection
`Maj+Tab`	Désindenter la sélection
`Ctrl+A`	Sélectionner le contenu de l'éditeur
`Ctrl+C`	Copier la sélection dans le presse-papier
`Ctrl+V`	Remplacer la sélection par le contenu du presse-papier
`Ctrl+X`	Supprimer la sélection et la copier dans le presse-papier
`Maj+Ctrl+R`	Chercher et remplacer une expression par une autre dans tout l'éditeur

AAV4_APP: Choisir et appliquer une technique de vérification

Des vérifications par jeux de tests sont proposées dans l'énoncé:

# initialisation
p = Stack()

# vérification 1
verif1 = empty(p)
print u'vérification 1 :',toString(p),verif1

for i in range(9) :
    push(p,i)
    print i, toString(p)

# vérification 2
verif2 = top(p) == pop(p)
print u'vérification 2 :',toString(p),verif2

# vérification 3
verif3 = pop(p) != top(p)
print u'vérification 3 :',toString(p),verif3

# vérification 4
x = 9
push(p,x)
verif4 = x == pop(p)
print u'vérification 4 :',toString(p),verif4

# vérification 5
p1 = toString(p)
push(p,pop(p))
p2 = toString(p)
verif5 = p1 == p2
print u'vérification 5 :',toString(p),verif5

# vérification 6
while not empty(p) :
    print pop(p),toString(p)

Files

Dans de nombreux cas, les seules opérations à effectuer sur les listes sont des insertions et des suppressions aux extrémités de la liste. C'est le cas en particulier des files (queue).

Exemple : file d'attente de voitures

A un péage, la première voiture à être entrée dans une file d'attente sera la première sortie de la file.

Définition : file

Une file est une séquence dans laquelle on ne peut ajouter un élément qu'à une seule extrémité et ne supprimer un élément qu'à l'autre extrémité : la « tête » de la file.

Dans le cas des files, on ajoute (on enfile) à une extrémité et on supprime (on défile) à l'autre extrémité. Une file est ainsi basée sur le principe « premier arrivé, premier sorti » (Fifo : First In, First Out) : le premier élément ajouté sera le premier à être récupéré en tête de file.

Les principales opérations nécessaires pour une file sont ainsi :

créer une file vide p:
p = Queue()
tester si la file p est vide:
ok = empty(p)
accéder à la tête x de la file p:
x = top(p)
enfiler un élément x en fin de la file p:
push(p,x)
défiler l'élément x de la tête de la pile p:
x = pop(p)
sérialiser une file p sous la forme d'une chaîne de caractères s ("[e1,e2...]"):
s = toString(p)

Définir les 6 fonctions précédentes concernant les files : Queue, empty, top, push, pop et toString. Une file sera implémentée par une liste.
Vérifier que :
1. empty(Queue()) == True
2. x == pop(p) and empty(p) après avoir effectué p = Queue(); push(p,x)

Votre réponse :

AAV4_APP: Résultat

Utiliser l'interpréteur Python ci-dessous pour programmer les fonctions demandées.

python : essai.py

Output

Interpréteur

Menu	Action
	Ré-initialiser les sorties
	Faire apparaître le menu d'aide
	Interpréter le programme

Editeur

Menu	Raccouci	Action
	`Ctrl+N`	Initialiser l'éditeur
	`Ctrl+O`	Charger le contenu d'un fichier dans l'éditeur
	`Ctrl+S`	Sauvegarder le contenu de l'éditeur dans un fichier
	`Ctrl+P`	Imprimer le contenu de l'éditeur
	`Ctrl+Z`	Annuler la dernière modification
	`Maj+Ctrl+Z`	Rétablir la modification précedente
	`Ctrl+F`	Chercher une expression dans l'éditeur
	`Maj+Ctrl+F`	Chercher et remplacer une expression par une autre
	`F10`	Ouvrir une documentation du langage

Raccourci	Action
`F1`	Afficher cette aide
`Tab`	Indenter la sélection
`Maj+Tab`	Désindenter la sélection
`Ctrl+A`	Sélectionner le contenu de l'éditeur
`Ctrl+C`	Copier la sélection dans le presse-papier
`Ctrl+V`	Remplacer la sélection par le contenu du presse-papier
`Ctrl+X`	Supprimer la sélection et la copier dans le presse-papier
`Maj+Ctrl+R`	Chercher et remplacer une expression par une autre dans tout l'éditeur

AAV4_APP: Vérification

Appliquer cette technique au résultat proposé.

Zone de saisie de texte

Clavier	Action
`F1`	Afficher une aide technique
`F2`	Afficher une aide pédagogique
`Ctrl-A`	Tout sélectionner
`Ctrl-C`	Copier la sélection dans le presse-papier
`Ctrl-V`	Copier le presse-papier dans la sélection
`Ctrl-X`	Couper la sélection et la copier dans le presse-papier
`Ctrl-Z`	Annuler la modification
`Maj-Ctrl-Z`	Rétablir la modification

Menu	Action
	Ré-initialiser les sorties
	Faire apparaître le menu d'aide
	Valider la zone de saisie
	Initialiser la zone de saisie
	Charger le contenu d'un fichier dans la zone de saisie
	Sauvegarder le contenu de la zone de saisie dans un fichier
	Imprimer le contenu de la zone de saisie

Une solution possible :

AAV4_APP: Répondre explicitement à la question posée

Les fonctions demandées sont définies ci-dessous :

python : appels-type-list-2.py

# -*- coding: utf-8 -*-

# définitions
def Queue() :
    u'''
    p = Queue()
    crée une file p vide
    '''
    return []

def empty(p) :
    u'''
    ok = empty(p)
    True si la file p est vide, False sinon.
    '''
    assert type(p) is list
    return len(p) == 0

def top(p) :
    u'''
    x = top(p)
    tête de la file p non vide.
    '''
    assert type(p) is list
    assert not empty(p)
    return p[len(p)-1]

def push(p,x) :
    u'''
    push(p,x)
    enfile x en fin de file p.
    '''
    assert type(p) is list
    p.insert(0,x)
    return

def pop(p) :
    u'''
    x = pop(p)
    défile par la tête la file p non vide.
    '''
    assert type(p) is list
    assert not empty(p)
    x = top(p)
    del p[len(p)-1]
    return x

def toString(p) :
    u'''
    s = toString(p)
    chaîne représentant la file p
    '''
    assert type(p) is list
    return str(p)

# vérifications
if __name__ == "__main__" :
    # initialisation
    p = Queue()

# vérification 1
    verif1 = empty(p) == True
    print u'vérification 1 :',toString(p),verif1

# vérification 2
    push(p,9)
    x = pop(p)
    verif2 = (x == 9) and empty(p)
    print toString(p),x,verif2

print toString(p)
    for i in range(9) :
        push(p,i)
        print i, toString(p)

verif3 = not empty(p)
    print u'vérification 3 :',toString(p),verif3

while not empty(p) :
        print pop(p),toString(p)

Output

Interpréteur

Menu	Action
	Ré-initialiser les sorties
	Faire apparaître le menu d'aide
	Interpréter le programme

Editeur

Menu	Raccouci	Action
	`Ctrl+N`	Initialiser l'éditeur
	`Ctrl+O`	Charger le contenu d'un fichier dans l'éditeur
	`Ctrl+S`	Sauvegarder le contenu de l'éditeur dans un fichier
	`Ctrl+P`	Imprimer le contenu de l'éditeur
	`Ctrl+Z`	Annuler la dernière modification
	`Maj+Ctrl+Z`	Rétablir la modification précedente
	`Ctrl+F`	Chercher une expression dans l'éditeur
	`Maj+Ctrl+F`	Chercher et remplacer une expression par une autre
	`F10`	Ouvrir une documentation du langage

Raccourci	Action
`F1`	Afficher cette aide
`Tab`	Indenter la sélection
`Maj+Tab`	Désindenter la sélection
`Ctrl+A`	Sélectionner le contenu de l'éditeur
`Ctrl+C`	Copier la sélection dans le presse-papier
`Ctrl+V`	Remplacer la sélection par le contenu du presse-papier
`Ctrl+X`	Supprimer la sélection et la copier dans le presse-papier
`Maj+Ctrl+R`	Chercher et remplacer une expression par une autre dans tout l'éditeur

AAV4_APP: Choisir et appliquer une technique de vérification

Des vérifications par jeux de tests sont proposées dans l'énoncé:

# initialisation
p = Queue()

# vérification 1
verif1 = empty(p) == True
print u'vérification 1 :',toString(p),verif1

# vérification 2
push(p,9)
x = pop(p)
verif2 = (x == 9) and empty(p)
print toString(p),x,verif2

# vérification 3
print toString(p)
for i in range(9) :
    push(p,i)
    print i, toString(p)

verif3 = not empty(p)
print u'vérification 3 :',toString(p),verif3

# vérification 4
while not empty(p) :
    print pop(p),toString(p)

Ensembles

Définition : ensemble

Un ensemble (set) est une collection d'éléments où chaque élément est unique.

Les principales opérations nécessaires pour un ensemble sont ainsi :

tester si x est unique dans la liste p:
ok = unique(p,x)
tester si une liste p peut être considérée comme un ensemble (ie. pas de doublons):
ok = isSet(p)
créer un ensemble vide p:
p = Set()
tester si l'ensemble p est vide:
ok = empty(p)
tester si x est élément de l'ensemble p:
ok = member(p,x)
ajouter un élément x à l'ensemble p:
insert(p,x)
L'élément ne sera pas ajouté s'il appartient déjà à l'ensemble (pas de doublons).
supprimer un élément x de l'ensemble p:
x = remove(p,x)
déterminer l'intersection de 2 ensembles p1 et p2:
p = inter(p1,p2)
déterminer l'union de 2 ensembles p1 et p2:
p = union(p1,p2)
déterminer la différence de 2 ensembles p1 et p2:
p = diff(p1,p2)
sérialiser une ensemble p sous la forme d'une chaîne de caractères s ("{e1,e2...}"):
s = toString(p)

Définir les 9 fonctions précédentes concernant les ensembles : Set, empty, member, insert, remove, inter, union, diff et toString. Un ensemble sera implémenté par une liste.
On vérifiera une à une les différentes opérations sur les ensembles.

Votre réponse :

AAV4_APP: Résultat

Utiliser l'interpréteur Python ci-dessous pour programmer les fonctions demandées.

python : essai.py

Output

Interpréteur

Menu	Action
	Ré-initialiser les sorties
	Faire apparaître le menu d'aide
	Interpréter le programme

Editeur

Menu	Raccouci	Action
	`Ctrl+N`	Initialiser l'éditeur
	`Ctrl+O`	Charger le contenu d'un fichier dans l'éditeur
	`Ctrl+S`	Sauvegarder le contenu de l'éditeur dans un fichier
	`Ctrl+P`	Imprimer le contenu de l'éditeur
	`Ctrl+Z`	Annuler la dernière modification
	`Maj+Ctrl+Z`	Rétablir la modification précedente
	`Ctrl+F`	Chercher une expression dans l'éditeur
	`Maj+Ctrl+F`	Chercher et remplacer une expression par une autre
	`F10`	Ouvrir une documentation du langage

Raccourci	Action
`F1`	Afficher cette aide
`Tab`	Indenter la sélection
`Maj+Tab`	Désindenter la sélection
`Ctrl+A`	Sélectionner le contenu de l'éditeur
`Ctrl+C`	Copier la sélection dans le presse-papier
`Ctrl+V`	Remplacer la sélection par le contenu du presse-papier
`Ctrl+X`	Supprimer la sélection et la copier dans le presse-papier
`Maj+Ctrl+R`	Chercher et remplacer une expression par une autre dans tout l'éditeur

AAV4_APP: Vérification

Appliquer cette technique au résultat proposé.

Zone de saisie de texte

Clavier	Action
`F1`	Afficher une aide technique
`F2`	Afficher une aide pédagogique
`Ctrl-A`	Tout sélectionner
`Ctrl-C`	Copier la sélection dans le presse-papier
`Ctrl-V`	Copier le presse-papier dans la sélection
`Ctrl-X`	Couper la sélection et la copier dans le presse-papier
`Ctrl-Z`	Annuler la modification
`Maj-Ctrl-Z`	Rétablir la modification

Menu	Action
	Ré-initialiser les sorties
	Faire apparaître le menu d'aide
	Valider la zone de saisie
	Initialiser la zone de saisie
	Charger le contenu d'un fichier dans la zone de saisie
	Sauvegarder le contenu de la zone de saisie dans un fichier
	Imprimer le contenu de la zone de saisie

Une solution possible :

AAV4_APP: Répondre explicitement à la question posée

Les fonctions demandées sont définies ci-dessous :

python : appels-type-list-3.py

# -*- coding: utf-8 -*-

# définitions
def unique(p,x) :
    u"""
    True si x est unique dans la liste p ou
    si x n'appartient pas à la liste p,
    False sinon.
    """
    assert type(p) is list
    n = p.count(x)
    if n > 1 :
        ok = False
    else :
        ok = True
    return ok

def isSet(p) :
    u"""
    ok = isSet(p)
    True si p est un ensemble, False sinon.
    """
    ok = True
    if type(p) is not list :
        ok = False
    else :
        i = 0
        while i < len(p) and ok :
            if not unique(p,p[i]) :
                ok = False
            else :
                i = i + 1
    return ok

def Set() :
    u"""
    p = Set()
    crée un ensemble p vide.
    """
    return []

def empty(p) :
    u"""
    ok = empty(p)
    True si l'ensemble p est vide, False sinon.
    """
    assert type(p) is list
    return len(p) == 0

def member(p,x) :
    u"""
    ok = member(p,x)
    True si x est un élément de p, False sinon.
    """
    assert isSet(p)
    return x in p

def add(p,x) :
    u"""
    ajoute l'élément x à l'ensemble p
    s'il n'est pas déjà un élément de p.
    """
    assert isSet(p)
    if x not in p : p.append(x)
    return

def remove(p,x) :
    u"""
    remove(p,x)
    supprime x de l'ensemble p.
    """
    assert isSet(p)
    p.remove(x)
    return

def inter(p1,p2) :
    u"""
    p = inter(p1,p2)
    ensemble, intersection des ensembles p1 et p2.
    """
    assert isSet(p1) and isSet(p2)
    p = Set()
    for elem in p1 :
        if elem in p2 :
            add(p,elem)
    return p

def union(p1,p2) :
    u"""
    p = union(p1,p2)
    ensemble, union des ensembles p1 et p2.
    """
    assert isSet(p1) and isSet(p2)
    p = Set()
    p = inter(p1,p2) + diff(p1,p2) + diff(p2,p1)
    return p

def diff(p1,p2) :
    u"""
    p = diff(p1,p2)
    ensemble, différence des ensembles p1 et p2.
    """
    assert isSet(p1) and isSet(p2)
    p = Set()
    for elem in p1 :
        if elem not in p2 :
            add(p,elem)
    return p

def toString(p) :
    u"""
    s = toString(p)
    chaîne représentant l'ensemble p.
    """
    assert type(p) is list
    return str(p)

# vérifications
if __name__ == "__main__" :
    # initialisation
    p1, p2 = Set(), Set()

# vérification 1
    verif1 = empty(p1) and empty(p2)
    print u'vérification 1 :',toString(p1),toString(p2),verif1

# vérification 2
    for i in range(5) :
        add(p1,i)
        add(p1,i)
        add(p2,i+3)
    verif2 = isSet(p1) and member(p1,4) and isSet(p2) and member(p2,7)
    print u'vérification 2 :',toString(p1),toString(p2),verif2

# vérification 3
    p3 = inter(p1,p2)
    p3.sort()
    verif3 = p3 == [3,4]
    print u'vérification 3 :',toString(p1),toString(p2),toString(p3),verif3

# vérification 4
    p4 = union(p1,p2)
    p4.sort()
    verif4 = p4 == [0,1,2,3,4,5,6,7]
    print u'vérification 4 :',toString(p1),toString(p2),toString(p4),verif4

# vérification 5
    p5 = diff(p1,p2)
    p5.sort()
    verif5 = p5 == [0,1,2]
    print u'vérification 5 :',toString(p1),toString(p2),toString(p5),verif5

# vérification 6
    p6 = diff(p2,p1)
    p6.sort()
    verif6 = p6 == [5,6,7]
    print u'vérification 6 :',toString(p1),toString(p2),toString(p6),verif6

# vérification 7
    for i in [5,6,7] :
        remove(p2,i)
    p2.sort()
    verif7 = p2 == p3
    print u'vérification 7 :',toString(p2),toString(p3),verif7

Output

Interpréteur

Menu	Action
	Ré-initialiser les sorties
	Faire apparaître le menu d'aide
	Interpréter le programme

Editeur

Menu	Raccouci	Action
	`Ctrl+N`	Initialiser l'éditeur
	`Ctrl+O`	Charger le contenu d'un fichier dans l'éditeur
	`Ctrl+S`	Sauvegarder le contenu de l'éditeur dans un fichier
	`Ctrl+P`	Imprimer le contenu de l'éditeur
	`Ctrl+Z`	Annuler la dernière modification
	`Maj+Ctrl+Z`	Rétablir la modification précedente
	`Ctrl+F`	Chercher une expression dans l'éditeur
	`Maj+Ctrl+F`	Chercher et remplacer une expression par une autre
	`F10`	Ouvrir une documentation du langage

Raccourci	Action
`F1`	Afficher cette aide
`Tab`	Indenter la sélection
`Maj+Tab`	Désindenter la sélection
`Ctrl+A`	Sélectionner le contenu de l'éditeur
`Ctrl+C`	Copier la sélection dans le presse-papier
`Ctrl+V`	Remplacer la sélection par le contenu du presse-papier
`Ctrl+X`	Supprimer la sélection et la copier dans le presse-papier
`Maj+Ctrl+R`	Chercher et remplacer une expression par une autre dans tout l'éditeur

AAV4_APP: Choisir et appliquer une technique de vérification

Des vérifications par jeux de tests sont proposées dans l'énoncé:

# initialisation
p1, p2 = Set(), Set()

# vérification 1
verif1 = empty(p1) and empty(p2)
print u'vérification 1 :',toString(p1),toString(p2),verif1

# vérification 2
for i in range(5) :
    add(p1,i)
    add(p1,i)
    add(p2,i+3)
verif2 = isSet(p1) and member(p1,4) and isSet(p2) and member(p2,7)
print u'vérification 2 :',toString(p1),toString(p2),verif2

# vérification 3
p3 = inter(p1,p2)
p3.sort()
verif3 = p3 == [3,4]
print u'vérification 3 :',toString(p1),toString(p2),toString(p3),verif3

# vérification 4
p4 = union(p1,p2)
p4.sort()
verif4 = p4 == [0,1,2,3,4,5,6,7]
print u'vérification 4 :',toString(p1),toString(p2),toString(p4),verif4

# vérification 5
p5 = diff(p1,p2)
p5.sort()
verif5 = p5 == [0,1,2]
print u'vérification 5 :',toString(p1),toString(p2),toString(p5),verif5

# vérification 6
p6 = diff(p2,p1)
p6.sort()
verif6 = p6 == [5,6,7]
print u'vérification 6 :',toString(p1),toString(p2),toString(p6),verif6

# vérification 7
for i in [5,6,7] :
    remove(p2,i)
p2.sort()
verif7 = p2 == p3
print u'vérification 7 :',toString(p2),toString(p3),verif7

Fleurs polygonales

Définir une fonction qui dessine une fleur à pétales polygonaux. Pour cela, on pourra décomposer le problème en 2 fonctions :

polygone(t,m,d) : la tortue t dessine un polygone régulier de m côtés de longueur d.

fleur(t,n,m,d) : la tortue t dessine une fleur composée de n pétales sous forme de n polygones réguliers de m cotés de longueur d tournés les uns par rapport aux autres de 360/n.

aide Python

Module turtle

Ce module permet de simuler la tortue Logo.

Exemple:

import turtle

t = turtle.Turtle()
s = turtle.Screen()
t.forward(100)
t.left(360./7)
s.exitonclick()

Classes :

Screen, Turtle

Méthodes :

Screen : addshape, bgcolor, bye, clear, clearscreen, delay, done, exitonclick, getshapes, listen, mainloop, onclick, onkey, onscreenclick, ontimer, register_shape, reset, resetscreen, setup, setworldcoordinates, tracer, turtles, update, window_height, window_width
Turtle : back, backward, begin_fill, bk, circle, clear, clone, color, degrees, delay, distance, done, dot, down, end_fill, fd, fill, fillcolor, forward, getpen, getscreen, getturtle, heading, hideturtle, home, ht, isdown, isvisible, left, lt, mainloop, onclick, ondrag, onrelease, pd, pencolor, pendown, pensize, penup, pos, position, pu, radians, reset, right, rt, seth, setheading, setpos, setposition, setundobuffer, setx, sety, shape, showturtle, speed, st, stamp, towards, tracer, undo, undobufferentries, up, update, width, window_height, window_width, write, xcor, ycor

Documentation officielle :

module turtle

Module random

Ce module permet de générer des nombres pseudo-aléatoires.

Exemple:

import random

n = random.randint(0,100)
e = random.choice([1,2,3,4,5,6])
p = random.random()

Fonctions :: choice, randint, random, randrange, seed, shuffle, uniform
Documentation officielle :: module random

Module math

Ce module permet de manipuler les principales fonctions mathématiques.

Exemple:

import math

pi = math.pi
y = math.log(math.sin(math.pi/2))

Constantes :: pi, e
Fonctions :: acos, acosh, asin, asinh, atan, atan2, atanh, ceil, copysign, cos, cosh, degrees, exp, fabs, factorial, floor, hypot, isnan, log, log10, pow, radians, sin, sinh, sqrt, tan, tanh, trunc
Documentation officielle :: module math

Votre réponse :

AAV4_APP: Résultat

Utiliser l'interpréteur Python ci-dessous pour programmer l'algorithme demandé.

python : essai.py

Output

Interpréteur

Menu	Action
	Ré-initialiser les sorties
	Faire apparaître le menu d'aide
	Interpréter le programme

Editeur

Menu	Raccouci	Action
	`Ctrl+N`	Initialiser l'éditeur
	`Ctrl+O`	Charger le contenu d'un fichier dans l'éditeur
	`Ctrl+S`	Sauvegarder le contenu de l'éditeur dans un fichier
	`Ctrl+P`	Imprimer le contenu de l'éditeur
	`Ctrl+Z`	Annuler la dernière modification
	`Maj+Ctrl+Z`	Rétablir la modification précedente
	`Ctrl+F`	Chercher une expression dans l'éditeur
	`Maj+Ctrl+F`	Chercher et remplacer une expression par une autre
	`F10`	Ouvrir une documentation du langage

Raccourci	Action
`F1`	Afficher cette aide
`Tab`	Indenter la sélection
`Maj+Tab`	Désindenter la sélection
`Ctrl+A`	Sélectionner le contenu de l'éditeur
`Ctrl+C`	Copier la sélection dans le presse-papier
`Ctrl+V`	Remplacer la sélection par le contenu du presse-papier
`Ctrl+X`	Supprimer la sélection et la copier dans le presse-papier
`Maj+Ctrl+R`	Chercher et remplacer une expression par une autre dans tout l'éditeur

AAV4_APP: Vérification

Appliquer cette technique au résultat proposé.

Zone de saisie de texte

Clavier	Action
`F1`	Afficher une aide technique
`F2`	Afficher une aide pédagogique
`Ctrl-A`	Tout sélectionner
`Ctrl-C`	Copier la sélection dans le presse-papier
`Ctrl-V`	Copier le presse-papier dans la sélection
`Ctrl-X`	Couper la sélection et la copier dans le presse-papier
`Ctrl-Z`	Annuler la modification
`Maj-Ctrl-Z`	Rétablir la modification

Menu	Action
	Ré-initialiser les sorties
	Faire apparaître le menu d'aide
	Valider la zone de saisie
	Initialiser la zone de saisie
	Charger le contenu d'un fichier dans la zone de saisie
	Sauvegarder le contenu de la zone de saisie dans un fichier
	Imprimer le contenu de la zone de saisie

Une solution possible :

AAV4_APP: Répondre explicitement à la question posée

Les fonctions demandées sont définies ci-dessous :

python : appels-logo-2.py

Output

Interpréteur

Menu	Action
	Ré-initialiser les sorties
	Faire apparaître le menu d'aide
	Interpréter le programme

Editeur

Menu	Raccouci	Action
	`Ctrl+N`	Initialiser l'éditeur
	`Ctrl+O`	Charger le contenu d'un fichier dans l'éditeur
	`Ctrl+S`	Sauvegarder le contenu de l'éditeur dans un fichier
	`Ctrl+P`	Imprimer le contenu de l'éditeur
	`Ctrl+Z`	Annuler la dernière modification
	`Maj+Ctrl+Z`	Rétablir la modification précedente
	`Ctrl+F`	Chercher une expression dans l'éditeur
	`Maj+Ctrl+F`	Chercher et remplacer une expression par une autre
	`F10`	Ouvrir une documentation du langage

Raccourci	Action
`F1`	Afficher cette aide
`Tab`	Indenter la sélection
`Maj+Tab`	Désindenter la sélection
`Ctrl+A`	Sélectionner le contenu de l'éditeur
`Ctrl+C`	Copier la sélection dans le presse-papier
`Ctrl+V`	Remplacer la sélection par le contenu du presse-papier
`Ctrl+X`	Supprimer la sélection et la copier dans le presse-papier
`Maj+Ctrl+R`	Chercher et remplacer une expression par une autre dans tout l'éditeur

AAV4_APP: Choisir et appliquer une technique de vérification

Des vérifications par jeux de tests sont proposées dans l'énoncé.

Le tracé de fleurs doit rendre compte de ce qu'est une fleur à pétales polygonaux:
```
import turtle
t = turtle.Turtle()
t.speed(10)
fleur(t,12,6,40)
```

Code de César

Le code de César est une méthode de cryptage très simple utilisée par Jules César dans ses correspondances secrètes.

Le texte crypté s'obtient en remplaçant chaque lettre du texte original par une lettre à distance fixe, toujours du même côté, dans l'ordre de l'alphabet. Dans un décalage à droite, on reprend au début de l'alphabet pour les dernières lettres de l'alphabet : ...x,y,z,a,b,c... Dans un décalage à gauche, on reprend à la fin de l'alphabet pour les premières lettres : ...c,b,a,z,y,x...

Exemples :

texte original décalage traduction

hal 1 ibm

kzbuoiorgzxgjaizout -6 etvoicilatraduction

nzopopufwpdnpdlc -11 codedejulescesar

ljvsluhapvuhslkpunluplbyzkliylza 19 ecolenationaledingenieursdebrest

Définir la fonction cesar(t,d) qui propose la traduction du texte original t lorsqu'on connaît le décalage d. On n'utilisera que les 26 lettres minuscules abcdef...xyz de l'alphabet.
Vérifier en appliquant 2 fois de suite la fonction cesar pour retrouver le texte original.

rappels sur le chiffrement

Chiffre de César

Le code de César est une méthode de cryptage où le texte crypté s'obtient en remplaçant chaque lettre du texte original par une lettre à distance fixe, toujours du même côté, dans l'ordre de l'alphabet. Dans un décalage à droite, on reprend au début de l'alphabet pour les dernières lettres de l'alphabet : ...x,y,z,a,b,c... Dans un décalage à gauche, on reprend à la fin de l'alphabet pour les premières lettres : ...c,b,a,z,y,x...
Chiffre de Trithemius

Johannes Trithemius (abbé bénédictin allemand, 1462-1516) proposa une amélioration du code de César où chaque lettre du texte original est décalée de 1 par rapport à la lettre précédente.

Ainsi, pour le texte original « bonjour », si la première lettre « b » est décalée de 3, la deuxième lettre « o » sera décalée de 4 (3+1), la troisième lettre « n » de 5 (4+1) et ainsi de suite jusqu’à la dernière lettre « r » qui sera finalement décalée de 9 (3+1+1+1+1+1+1).
Chiffre de Vigenère

Blaise de Vigenère (diplomate français, 1523-1596) proposa une amélioration du chiffre de Trithemius où chaque lettre t[i] du texte original t est décalée de k[i%len(k)] lettres si k est la clé de chiffrement. Les 26 lettres abc...yz sont numérotées de 0 (a) à 25 (z).

Ainsi, pour le texte original « bonjour » et la clé « azerty », la première lettre « b » sera décalée de 0 (la première lettre de la clé : « a » vaut 0), la deuxième lettre « o » sera décalée de 25 (la deuxième lettre de la clé : « z » vaut 25), la troisième lettre « n » de 4 (la troisième lettre de la clé : « e » vaut 4) et ainsi de suite jusqu’à la septième et dernière lettre « r » qui sera finalement décalée de 0 (k[i%len(k)] = k[6%6] = k[0] : « a » vaut 0).

Votre réponse :

AAV4_APP: Résultat

Utiliser l'interpréteur Python ci-dessous pour programmer l'algorithme demandé.

python : essai.py

Output

Interpréteur

Menu	Action
	Ré-initialiser les sorties
	Faire apparaître le menu d'aide
	Interpréter le programme

Editeur

Menu	Raccouci	Action
	`Ctrl+N`	Initialiser l'éditeur
	`Ctrl+O`	Charger le contenu d'un fichier dans l'éditeur
	`Ctrl+S`	Sauvegarder le contenu de l'éditeur dans un fichier
	`Ctrl+P`	Imprimer le contenu de l'éditeur
	`Ctrl+Z`	Annuler la dernière modification
	`Maj+Ctrl+Z`	Rétablir la modification précedente
	`Ctrl+F`	Chercher une expression dans l'éditeur
	`Maj+Ctrl+F`	Chercher et remplacer une expression par une autre
	`F10`	Ouvrir une documentation du langage

Raccourci	Action
`F1`	Afficher cette aide
`Tab`	Indenter la sélection
`Maj+Tab`	Désindenter la sélection
`Ctrl+A`	Sélectionner le contenu de l'éditeur
`Ctrl+C`	Copier la sélection dans le presse-papier
`Ctrl+V`	Remplacer la sélection par le contenu du presse-papier
`Ctrl+X`	Supprimer la sélection et la copier dans le presse-papier
`Maj+Ctrl+R`	Chercher et remplacer une expression par une autre dans tout l'éditeur

AAV4_APP: Vérification

Appliquer cette technique au résultat proposé.

Zone de saisie de texte

Clavier	Action
`F1`	Afficher une aide technique
`F2`	Afficher une aide pédagogique
`Ctrl-A`	Tout sélectionner
`Ctrl-C`	Copier la sélection dans le presse-papier
`Ctrl-V`	Copier le presse-papier dans la sélection
`Ctrl-X`	Couper la sélection et la copier dans le presse-papier
`Ctrl-Z`	Annuler la modification
`Maj-Ctrl-Z`	Rétablir la modification

Menu	Action
	Ré-initialiser les sorties
	Faire apparaître le menu d'aide
	Valider la zone de saisie
	Initialiser la zone de saisie
	Charger le contenu d'un fichier dans la zone de saisie
	Sauvegarder le contenu de la zone de saisie dans un fichier
	Imprimer le contenu de la zone de saisie

Une solution possible :

AAV4_APP: Répondre explicitement à la question posée

Les fonctions demandées sont définies ci-dessous :

python : appels-jeux-1.py

Output

Interpréteur

Menu	Action
	Ré-initialiser les sorties
	Faire apparaître le menu d'aide
	Interpréter le programme

Editeur

Menu	Raccouci	Action
	`Ctrl+N`	Initialiser l'éditeur
	`Ctrl+O`	Charger le contenu d'un fichier dans l'éditeur
	`Ctrl+S`	Sauvegarder le contenu de l'éditeur dans un fichier
	`Ctrl+P`	Imprimer le contenu de l'éditeur
	`Ctrl+Z`	Annuler la dernière modification
	`Maj+Ctrl+Z`	Rétablir la modification précedente
	`Ctrl+F`	Chercher une expression dans l'éditeur
	`Maj+Ctrl+F`	Chercher et remplacer une expression par une autre
	`F10`	Ouvrir une documentation du langage

Raccourci	Action
`F1`	Afficher cette aide
`Tab`	Indenter la sélection
`Maj+Tab`	Désindenter la sélection
`Ctrl+A`	Sélectionner le contenu de l'éditeur
`Ctrl+C`	Copier la sélection dans le presse-papier
`Ctrl+V`	Remplacer la sélection par le contenu du presse-papier
`Ctrl+X`	Supprimer la sélection et la copier dans le presse-papier
`Maj+Ctrl+R`	Chercher et remplacer une expression par une autre dans tout l'éditeur

AAV4_APP: Choisir et appliquer une technique de vérification

Des vérifications par jeux de tests sont proposées dans l'énoncé:

tests = [('hal',1,'ibm'),
         ('kzbuoiorgzxgjaizout',-6,'etvoicilatraduction'),
         ('nzopopufwpdnpdlc',-11,'codedejulescesar'),
         ('ljvsluhapvuhslkpunluplbyzkliylza',19,'ecolenationaledingenieursdebrest'),
         ('',-158,''),
         ('pareil',0,'pareil')]
for (e1,e2,s1) in tests :
    r = cesar(e1,e2)
    verif1 = (r == s1)
    s = cesar(cesar(e1,e2),-e2)
    verif2 = (e1 == s)
    print e1,e2,r,s,verif1,verif2

Le double appel cesar(cesar(t,d),-d) redonne bien le texte original t.

Chiffre de Trithemius

Johannes Trithemius (abbé bénédictin allemand, 1462-1516) proposa une amélioration du code de César où chaque lettre du texte original est décalée de 1 par rapport à la lettre précédente.

Ainsi, pour le texte original « bonjour », si la première lettre « b » est décalée de 3, la deuxième lettre « o » sera décalée de 4 (3+1), la troisième lettre « n » de 5 (4+1) et ainsi de suite jusqu'à la dernière lettre « r » qui sera finalement décalée de 9 (3+1+1+1+1+1+1).

Exemples :

texte original décalage initial décalage à chaque étape traduction

hal 1 1 ico

kbfawsafwrrchakducd -6 -2 etvoicilatraduction

nwigcamhvdoingpk -11 3 codedetrithemius

lndebofcvfizoloxgdfsrrlmrglmgxpu 19 -4 ecolenationaledingenieursdebrest

Définir la fonction trithemius(t,d,s) qui propose la traduction du texte original t en appliquant un décalage initial de d lettres et en ajoutant s lettres à chaque étape. On n'utilisera que les 26 lettres minuscules abcdef...xyz de l'alphabet.
Vérifier en appliquant 2 fois de suite la fonction trithemius pour retrouver le texte original.

rappels sur le chiffrement

Chiffre de César

Le code de César est une méthode de cryptage où le texte crypté s'obtient en remplaçant chaque lettre du texte original par une lettre à distance fixe, toujours du même côté, dans l'ordre de l'alphabet. Dans un décalage à droite, on reprend au début de l'alphabet pour les dernières lettres de l'alphabet : ...x,y,z,a,b,c... Dans un décalage à gauche, on reprend à la fin de l'alphabet pour les premières lettres : ...c,b,a,z,y,x...
Chiffre de Trithemius

Johannes Trithemius (abbé bénédictin allemand, 1462-1516) proposa une amélioration du code de César où chaque lettre du texte original est décalée de 1 par rapport à la lettre précédente.

Ainsi, pour le texte original « bonjour », si la première lettre « b » est décalée de 3, la deuxième lettre « o » sera décalée de 4 (3+1), la troisième lettre « n » de 5 (4+1) et ainsi de suite jusqu’à la dernière lettre « r » qui sera finalement décalée de 9 (3+1+1+1+1+1+1).
Chiffre de Vigenère

Blaise de Vigenère (diplomate français, 1523-1596) proposa une amélioration du chiffre de Trithemius où chaque lettre t[i] du texte original t est décalée de k[i%len(k)] lettres si k est la clé de chiffrement. Les 26 lettres abc...yz sont numérotées de 0 (a) à 25 (z).

Ainsi, pour le texte original « bonjour » et la clé « azerty », la première lettre « b » sera décalée de 0 (la première lettre de la clé : « a » vaut 0), la deuxième lettre « o » sera décalée de 25 (la deuxième lettre de la clé : « z » vaut 25), la troisième lettre « n » de 4 (la troisième lettre de la clé : « e » vaut 4) et ainsi de suite jusqu’à la septième et dernière lettre « r » qui sera finalement décalée de 0 (k[i%len(k)] = k[6%6] = k[0] : « a » vaut 0).

Votre réponse :

AAV4_APP: Résultat

Utiliser l'interpréteur Python ci-dessous pour programmer l'algorithme demandé.

python : essai.py

Output

Interpréteur

Menu	Action
	Ré-initialiser les sorties
	Faire apparaître le menu d'aide
	Interpréter le programme

Editeur

Menu	Raccouci	Action
	`Ctrl+N`	Initialiser l'éditeur
	`Ctrl+O`	Charger le contenu d'un fichier dans l'éditeur
	`Ctrl+S`	Sauvegarder le contenu de l'éditeur dans un fichier
	`Ctrl+P`	Imprimer le contenu de l'éditeur
	`Ctrl+Z`	Annuler la dernière modification
	`Maj+Ctrl+Z`	Rétablir la modification précedente
	`Ctrl+F`	Chercher une expression dans l'éditeur
	`Maj+Ctrl+F`	Chercher et remplacer une expression par une autre
	`F10`	Ouvrir une documentation du langage

Raccourci	Action
`F1`	Afficher cette aide
`Tab`	Indenter la sélection
`Maj+Tab`	Désindenter la sélection
`Ctrl+A`	Sélectionner le contenu de l'éditeur
`Ctrl+C`	Copier la sélection dans le presse-papier
`Ctrl+V`	Remplacer la sélection par le contenu du presse-papier
`Ctrl+X`	Supprimer la sélection et la copier dans le presse-papier
`Maj+Ctrl+R`	Chercher et remplacer une expression par une autre dans tout l'éditeur

AAV4_APP: Vérification

Appliquer cette technique au résultat proposé.

Zone de saisie de texte

Clavier	Action
`F1`	Afficher une aide technique
`F2`	Afficher une aide pédagogique
`Ctrl-A`	Tout sélectionner
`Ctrl-C`	Copier la sélection dans le presse-papier
`Ctrl-V`	Copier le presse-papier dans la sélection
`Ctrl-X`	Couper la sélection et la copier dans le presse-papier
`Ctrl-Z`	Annuler la modification
`Maj-Ctrl-Z`	Rétablir la modification

Menu	Action
	Ré-initialiser les sorties
	Faire apparaître le menu d'aide
	Valider la zone de saisie
	Initialiser la zone de saisie
	Charger le contenu d'un fichier dans la zone de saisie
	Sauvegarder le contenu de la zone de saisie dans un fichier
	Imprimer le contenu de la zone de saisie

Une solution possible :

AAV4_APP: Répondre explicitement à la question posée

Les fonctions demandées sont définies ci-dessous :

python : appels-jeux-2.py

# -*- coding: utf-8 -*-

# définitions
def trithemius(t,d,s) :
    u"""
    traduction = trithemius(t,d,s)
    traduction du texte t selon la méthode de Trithemius
    en appliquant un décalage initial de d lettres
    et en ajoutant s lettres à chaque étape.
    """
    assert type(t) is str
    assert type(d) is int
    debut, fin = ord('a'), ord('z')
    i, traduction = 0, ""
    while i < len(t) :
        c = t[i]
        code = (ord(c)-debut + d)%(fin-debut+1) + debut
        traduction = traduction + chr(code)
        d = d + s
        i = i + 1
    return traduction

# vérification
tests = [('hal',1,1,'ico'),
         ('kbfawsafwrrchakducd',-6,-2,'etvoicilatraduction'),
         ('nwigcamhvdoingpk',-11,3,'codedetrithemius'),
         ('lndebofcvfizoloxgdfsrrlmrglmgxpu',19,-4,'ecolenationaledingenieursdebrest'),
         ('',-158,-2,''),
         ('pareil',0,0,'pareil')]
for (e1,e2,e3,s1) in tests :
    r = trithemius(e1,e2,e3)
    verif1 = (r == s1)
    s = trithemius(trithemius(e1,e2,e3),-e2,-e3)
    verif2 = (e1 == s)
    print e1,e2,e3,r,s,verif1,verif2

Output

Interpréteur

Menu	Action
	Ré-initialiser les sorties
	Faire apparaître le menu d'aide
	Interpréter le programme

Editeur

Menu	Raccouci	Action
	`Ctrl+N`	Initialiser l'éditeur
	`Ctrl+O`	Charger le contenu d'un fichier dans l'éditeur
	`Ctrl+S`	Sauvegarder le contenu de l'éditeur dans un fichier
	`Ctrl+P`	Imprimer le contenu de l'éditeur
	`Ctrl+Z`	Annuler la dernière modification
	`Maj+Ctrl+Z`	Rétablir la modification précedente
	`Ctrl+F`	Chercher une expression dans l'éditeur
	`Maj+Ctrl+F`	Chercher et remplacer une expression par une autre
	`F10`	Ouvrir une documentation du langage

Raccourci	Action
`F1`	Afficher cette aide
`Tab`	Indenter la sélection
`Maj+Tab`	Désindenter la sélection
`Ctrl+A`	Sélectionner le contenu de l'éditeur
`Ctrl+C`	Copier la sélection dans le presse-papier
`Ctrl+V`	Remplacer la sélection par le contenu du presse-papier
`Ctrl+X`	Supprimer la sélection et la copier dans le presse-papier
`Maj+Ctrl+R`	Chercher et remplacer une expression par une autre dans tout l'éditeur

AAV4_APP: Choisir et appliquer une technique de vérification

Des vérifications par jeux de tests sont proposées dans l'énoncé:

tests = [('hal',1,1,'ico'),
         ('kbfawsafwrrchakducd',-6,-2,'etvoicilatraduction'),
         ('nwigcamhvdoingpk',-11,3,'codedetrithemius'),
         ('lndebofcvfizoloxgdfsrrlmrglmgxpu',19,-4,'ecolenationaledingenieursdebrest'),
         ('',-158,-2,''),
         ('pareil',0,0,'pareil')]
for (e1,e2,e3,s1) in tests :
    r = trithemius(e1,e2,e3)
    verif1 = (r == s1)
    s = trithemius(trithemius(e1,e2,e3),-e2,-e3)
    verif2 = (e1 == s)
    print e1,e2,e3,r,s,verif1,verif2

Le double appel trithemius(trithemius(t,d,s),-d,-s) redonne bien le texte original t.

Chiffre de Vigenère

Blaise de Vigenère (diplomate français, 1523-1596) proposa une amélioration du chiffre de Trithemius où chaque lettre t[i] du texte original t est décalée de k[i%len(k)] lettres si k est la clé de chiffrement. Les 26 lettres abc...yz sont numérotées de 0 (a) à 25 (z).

Ainsi, pour le texte original « bonjour » et la clé « azerty », la première lettre « b » sera décalée de 0 (la première lettre de la clé : « a » vaut 0), la deuxième lettre « o » sera décalée de 25 (la deuxième lettre de la clé : « z » vaut 25), la troisième lettre « n » de 4 (la troisième lettre de la clé : « e » vaut 4) et ainsi de suite jusqu'à la septième et dernière lettre « r » qui sera finalement décalée de 0 (k[i%len(k)] = k[6%6] = k[0] : « a » vaut 0).

Exemples :

texte original clé traduction

hal enibook lnt

agnnuoyhnlqmpkyganz enibook etvoicilatraduction

gblfrsfmtmosfo enibook codedevigenere

apgkqzqpvgmmxuzvffqzyahjrpqrnrks enibook ecolenationaledingenieursdebrest

bonjour azerty bnrahsr

Définir la fonction vigenere(t,k,s) qui propose la traduction du texte original t selon la méthode de Vigenère en utilisant la clé k dans le sens s (+1 ou -1). On n'utilisera que les 26 lettres minuscules abcdef...xyz de l'alphabet.
Vérifier en appliquant 2 fois de suite la fonction vigenere pour retrouver le texte original.

rappels sur le chiffrement

Chiffre de César

Le code de César est une méthode de cryptage où le texte crypté s'obtient en remplaçant chaque lettre du texte original par une lettre à distance fixe, toujours du même côté, dans l'ordre de l'alphabet. Dans un décalage à droite, on reprend au début de l'alphabet pour les dernières lettres de l'alphabet : ...x,y,z,a,b,c... Dans un décalage à gauche, on reprend à la fin de l'alphabet pour les premières lettres : ...c,b,a,z,y,x...
Chiffre de Trithemius

Johannes Trithemius (abbé bénédictin allemand, 1462-1516) proposa une amélioration du code de César où chaque lettre du texte original est décalée de 1 par rapport à la lettre précédente.

Ainsi, pour le texte original « bonjour », si la première lettre « b » est décalée de 3, la deuxième lettre « o » sera décalée de 4 (3+1), la troisième lettre « n » de 5 (4+1) et ainsi de suite jusqu’à la dernière lettre « r » qui sera finalement décalée de 9 (3+1+1+1+1+1+1).
Chiffre de Vigenère

Blaise de Vigenère (diplomate français, 1523-1596) proposa une amélioration du chiffre de Trithemius où chaque lettre t[i] du texte original t est décalée de k[i%len(k)] lettres si k est la clé de chiffrement. Les 26 lettres abc...yz sont numérotées de 0 (a) à 25 (z).

Ainsi, pour le texte original « bonjour » et la clé « azerty », la première lettre « b » sera décalée de 0 (la première lettre de la clé : « a » vaut 0), la deuxième lettre « o » sera décalée de 25 (la deuxième lettre de la clé : « z » vaut 25), la troisième lettre « n » de 4 (la troisième lettre de la clé : « e » vaut 4) et ainsi de suite jusqu’à la septième et dernière lettre « r » qui sera finalement décalée de 0 (k[i%len(k)] = k[6%6] = k[0] : « a » vaut 0).

Votre réponse :

AAV4_APP: Résultat

Utiliser l'interpréteur Python ci-dessous pour programmer l'algorithme demandé.

python : essai.py

Output

Interpréteur

Menu	Action
	Ré-initialiser les sorties
	Faire apparaître le menu d'aide
	Interpréter le programme

Editeur

Menu	Raccouci	Action
	`Ctrl+N`	Initialiser l'éditeur
	`Ctrl+O`	Charger le contenu d'un fichier dans l'éditeur
	`Ctrl+S`	Sauvegarder le contenu de l'éditeur dans un fichier
	`Ctrl+P`	Imprimer le contenu de l'éditeur
	`Ctrl+Z`	Annuler la dernière modification
	`Maj+Ctrl+Z`	Rétablir la modification précedente
	`Ctrl+F`	Chercher une expression dans l'éditeur
	`Maj+Ctrl+F`	Chercher et remplacer une expression par une autre
	`F10`	Ouvrir une documentation du langage

Raccourci	Action
`F1`	Afficher cette aide
`Tab`	Indenter la sélection
`Maj+Tab`	Désindenter la sélection
`Ctrl+A`	Sélectionner le contenu de l'éditeur
`Ctrl+C`	Copier la sélection dans le presse-papier
`Ctrl+V`	Remplacer la sélection par le contenu du presse-papier
`Ctrl+X`	Supprimer la sélection et la copier dans le presse-papier
`Maj+Ctrl+R`	Chercher et remplacer une expression par une autre dans tout l'éditeur

AAV4_APP: Vérification

Appliquer cette technique au résultat proposé.

Zone de saisie de texte

Clavier	Action
`F1`	Afficher une aide technique
`F2`	Afficher une aide pédagogique
`Ctrl-A`	Tout sélectionner
`Ctrl-C`	Copier la sélection dans le presse-papier
`Ctrl-V`	Copier le presse-papier dans la sélection
`Ctrl-X`	Couper la sélection et la copier dans le presse-papier
`Ctrl-Z`	Annuler la modification
`Maj-Ctrl-Z`	Rétablir la modification

Menu	Action
	Ré-initialiser les sorties
	Faire apparaître le menu d'aide
	Valider la zone de saisie
	Initialiser la zone de saisie
	Charger le contenu d'un fichier dans la zone de saisie
	Sauvegarder le contenu de la zone de saisie dans un fichier
	Imprimer le contenu de la zone de saisie

Une solution possible :

AAV4_APP: Répondre explicitement à la question posée

Les fonctions demandées sont définies ci-dessous :

python : appels-jeux-3.py

# -*- coding: utf-8 -*-

# définitions
def vigenere(t,k,s) :
    u"""
    traduction = vigenere(t,k,s)
    traduction du texte t selon la méthode de Vigenère
    en utilisant la clé k dans le sens s (+1 ou -1).
    """
    assert type(t) is str
    assert type(k) is str
    assert type(s) is int
    assert s == 1 or s == -1
    debut, fin = ord('a'), ord('z')
    i, traduction = 0, ""
    while i < len(t) :
        c = t[i]
        ck = k[i%len(k)]
        code = (ord(c)-debut + s*(ord(ck)-debut))%(fin-debut+1) + debut
        traduction = traduction + chr(code)
        i = i + 1
    return traduction

# vérification
tests = [('hal','enibook',1,'lnt'),
         ('agnnuoyhnlqmpkyganz','enibook',1,'etvoicilatraduction'),
         ('gblfrsfmtmosfo','enibook',-1,'codedevigenere'),
         ('apgkqzqpvgmmxuzvffqzyahjrpqrnrks','enibook',1,'ecolenationaledingenieursdebrest'),
         ('','enibook',1,''),
         ('pareil','enibook',1,'tnzfwz')]
for (e1,e2,e3,s1) in tests :
    r = vigenere(e1,e2,e3)
    verif1 = (r == s1)
    s = vigenere(vigenere(e1,e2,e3),e2,-e3)
    verif2 = (e1 == s)
    print e1,e2,e3,r,s,verif1,verif2

Output

Interpréteur

Menu	Action
	Ré-initialiser les sorties
	Faire apparaître le menu d'aide
	Interpréter le programme

Editeur

Menu	Raccouci	Action
	`Ctrl+N`	Initialiser l'éditeur
	`Ctrl+O`	Charger le contenu d'un fichier dans l'éditeur
	`Ctrl+S`	Sauvegarder le contenu de l'éditeur dans un fichier
	`Ctrl+P`	Imprimer le contenu de l'éditeur
	`Ctrl+Z`	Annuler la dernière modification
	`Maj+Ctrl+Z`	Rétablir la modification précedente
	`Ctrl+F`	Chercher une expression dans l'éditeur
	`Maj+Ctrl+F`	Chercher et remplacer une expression par une autre
	`F10`	Ouvrir une documentation du langage

Raccourci	Action
`F1`	Afficher cette aide
`Tab`	Indenter la sélection
`Maj+Tab`	Désindenter la sélection
`Ctrl+A`	Sélectionner le contenu de l'éditeur
`Ctrl+C`	Copier la sélection dans le presse-papier
`Ctrl+V`	Remplacer la sélection par le contenu du presse-papier
`Ctrl+X`	Supprimer la sélection et la copier dans le presse-papier
`Maj+Ctrl+R`	Chercher et remplacer une expression par une autre dans tout l'éditeur

AAV4_APP: Choisir et appliquer une technique de vérification

Des vérifications par jeux de tests sont proposées dans l'énoncé:

tests = [('hal','enibook',1,'lnt'),
         ('agnnuoyhnlqmpkyganz','enibook',1,'etvoicilatraduction'),
         ('gblfrsfmtmosfo','enibook',-1,'codedevigenere'),
         ('apgkqzqpvgmmxuzvffqzyahjrpqrnrks','enibook',1,'ecolenationaledingenieursdebrest'),
         ('','enibook',1,''),
         ('pareil','enibook',1,'tnzfwz')]
for (e1,e2,e3,s1) in tests :
    r = vigenere(e1,e2,e3)
    verif1 = (r == s1)
    s = vigenere(vigenere(e1,e2,e3),e2,-e3)
    verif2 = (e1 == s)
    print e1,e2,e3,r,s,verif1,verif2

Le double appel vigenere(vigenere(t,k,s),k,-s) redonne bien le texte original t.

Ensembles « en compréhension »

En mathématiques un sous-ensemble d'un ensemble \(E\) peut être défini « en compréhension » par \(\{x \in E | P(x) \}\) : le sous-ensemble des éléments \(x\) de \(E\) vérifiant la propriété \(P\).

Exemples :

sous-ensemble définition en compréhension

entiers impairs \(\{n \in \mathbb{N} | n \mod 2 = 1 \}\)

entiers pairs \(\{n \in \mathbb{N} | n \mod 2 = 0 \}\)

entiers carrés parfaits non nuls \(\{n \in \mathbb{N} | \exists y \in \mathbb{N}\ (y > 0 \mathrm{\ et\ } x = y^2)\}\)

entiers relatifs dans \([-4,+4]\) \(\{n \in \mathbb{N} | -4 \leq n \leq +4 \}\)

points \((x,y)\) du plan situés sur une droite de pente \(a\) et d'ordonnée à l'origine \(b\) \(\{(x,y) \in \mathbb{R}^2 | y = ax + b \}\)

En utilisant les listes « en compréhension » de Python, définir les opérations ensemblistes suivantes :

l'intersection de 2 ensembles p1 et p2:
p = inter(p1,p2)
la différence de 2 ensembles p1 et p2:
p = diff(p1,p2)
puis:
p = diff(p2,p1)
l'union de 2 ensembles p1 et p2:
p = union(p1,p2)

aide Python

Certains langages comme Python proposent des listes « en compréhension », des listes dont les éléments sont définis par filtrage du contenu d'une autre liste. En Python, la syntaxe est la suivante:

[f(x) for x in E if P(x)]

Cette expression est une liste qui contient les éléments f(x) où x est un élément de E qui vérifient la propriété P:

# E : liste des 10 premiers entiers
>>> E = range(10)
>>> E
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

# liste inchangée (le test ``if P(x)`` est facultatif)
>>> [x for x in E]
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

# liste des carrés des éléments de E
>>> [x*x for x in E]
[0, 1, 4, 9, 16, 25, 36, 49, 64, 81]

# liste des nombres pairs dans E
>>> [x for x in E if x%2 == 0]
[0, 2, 4, 6, 8]

# liste des carrés des nombres pairs dans E
>>> [x*x for x in E if x%2 == 0]
[0, 4, 16, 36, 64]

# liste des nombres positifs multiples de 4 dans E
>>> [x for x in E if x > 0 and x%4 == 0]
[4, 8]

Votre réponse :

AAV4_APP: Résultat

Utiliser l'interpréteur Python ci-dessous pour programmer l'algorithme demandé.

python : essai.py

Output

Interpréteur

Menu	Action
	Ré-initialiser les sorties
	Faire apparaître le menu d'aide
	Interpréter le programme

Editeur

Menu	Raccouci	Action
	`Ctrl+N`	Initialiser l'éditeur
	`Ctrl+O`	Charger le contenu d'un fichier dans l'éditeur
	`Ctrl+S`	Sauvegarder le contenu de l'éditeur dans un fichier
	`Ctrl+P`	Imprimer le contenu de l'éditeur
	`Ctrl+Z`	Annuler la dernière modification
	`Maj+Ctrl+Z`	Rétablir la modification précedente
	`Ctrl+F`	Chercher une expression dans l'éditeur
	`Maj+Ctrl+F`	Chercher et remplacer une expression par une autre
	`F10`	Ouvrir une documentation du langage

Raccourci	Action
`F1`	Afficher cette aide
`Tab`	Indenter la sélection
`Maj+Tab`	Désindenter la sélection
`Ctrl+A`	Sélectionner le contenu de l'éditeur
`Ctrl+C`	Copier la sélection dans le presse-papier
`Ctrl+V`	Remplacer la sélection par le contenu du presse-papier
`Ctrl+X`	Supprimer la sélection et la copier dans le presse-papier
`Maj+Ctrl+R`	Chercher et remplacer une expression par une autre dans tout l'éditeur

AAV4_APP: Vérification

Appliquer cette technique au résultat proposé.

Zone de saisie de texte

Clavier	Action
`F1`	Afficher une aide technique
`F2`	Afficher une aide pédagogique
`Ctrl-A`	Tout sélectionner
`Ctrl-C`	Copier la sélection dans le presse-papier
`Ctrl-V`	Copier le presse-papier dans la sélection
`Ctrl-X`	Couper la sélection et la copier dans le presse-papier
`Ctrl-Z`	Annuler la modification
`Maj-Ctrl-Z`	Rétablir la modification

Menu	Action
	Ré-initialiser les sorties
	Faire apparaître le menu d'aide
	Valider la zone de saisie
	Initialiser la zone de saisie
	Charger le contenu d'un fichier dans la zone de saisie
	Sauvegarder le contenu de la zone de saisie dans un fichier
	Imprimer le contenu de la zone de saisie

Une solution possible :

AAV4_APP: Répondre explicitement à la question posée

Les fonctions demandées sont définies ci-dessous :

python : appels-prop-1.py

Output

Interpréteur

Menu	Action
	Ré-initialiser les sorties
	Faire apparaître le menu d'aide
	Interpréter le programme

Editeur

Menu	Raccouci	Action
	`Ctrl+N`	Initialiser l'éditeur
	`Ctrl+O`	Charger le contenu d'un fichier dans l'éditeur
	`Ctrl+S`	Sauvegarder le contenu de l'éditeur dans un fichier
	`Ctrl+P`	Imprimer le contenu de l'éditeur
	`Ctrl+Z`	Annuler la dernière modification
	`Maj+Ctrl+Z`	Rétablir la modification précedente
	`Ctrl+F`	Chercher une expression dans l'éditeur
	`Maj+Ctrl+F`	Chercher et remplacer une expression par une autre
	`F10`	Ouvrir une documentation du langage

Raccourci	Action
`F1`	Afficher cette aide
`Tab`	Indenter la sélection
`Maj+Tab`	Désindenter la sélection
`Ctrl+A`	Sélectionner le contenu de l'éditeur
`Ctrl+C`	Copier la sélection dans le presse-papier
`Ctrl+V`	Remplacer la sélection par le contenu du presse-papier
`Ctrl+X`	Supprimer la sélection et la copier dans le presse-papier
`Maj+Ctrl+R`	Chercher et remplacer une expression par une autre dans tout l'éditeur

AAV4_APP: Choisir et appliquer une technique de vérification

Une simple vérification par calcul « à la main » suffira ici:

e1, e2 = [1,2,5,6,7], [0,2,3,4,6,8]
print u'intersection     :',inter(e1,e2)
print u'différence e1-e2 :',diff(e1,e2)
print u'différence e2-e1 :',diff(e2,e1)
print u'union            :',union(e1,e2)

texte original	décalage	traduction
`hal`	1	`ibm`
`kzbuoiorgzxgjaizout`	-6	`etvoicilatraduction`
`nzopopufwpdnpdlc`	-11	`codedejulescesar`
`ljvsluhapvuhslkpunluplbyzkliylza`	19	`ecolenationaledingenieursdebrest`

texte original	décalage initial	décalage à chaque étape	traduction
`hal`	1	1	`ico`
`kbfawsafwrrchakducd`	-6	-2	`etvoicilatraduction`
`nwigcamhvdoingpk`	-11	3	`codedetrithemius`
`lndebofcvfizoloxgdfsrrlmrglmgxpu`	19	-4	`ecolenationaledingenieursdebrest`

texte original	clé	traduction
`hal`	`enibook`	`lnt`
`agnnuoyhnlqmpkyganz`	`enibook`	`etvoicilatraduction`
`gblfrsfmtmosfo`	`enibook`	`codedevigenere`
`apgkqzqpvgmmxuzvffqzyahjrpqrnrks`	`enibook`	`ecolenationaledingenieursdebrest`
`bonjour`	`azerty`	`bnrahsr`

sous-ensemble	définition en compréhension
entiers impairs	\(\{n \in \mathbb{N} \| n \mod 2 = 1 \}\)
entiers pairs	\(\{n \in \mathbb{N} \| n \mod 2 = 0 \}\)
entiers carrés parfaits non nuls	\(\{n \in \mathbb{N} \| \exists y \in \mathbb{N}\ (y > 0 \mathrm{\ et\ } x = y^2)\}\)
entiers relatifs dans \([-4,+4]\)	\(\{n \in \mathbb{N} \| -4 \leq n \leq +4 \}\)
points \((x,y)\) du plan situés sur une droite de pente \(a\) et d'ordonnée à l'origine \(b\)	\(\{(x,y) \in \mathbb{R}^2 \| y = ax + b \}\)

Fichier de rejeu Close

Indication Close

A propos de... Close

Commentaire Close

Algorithmique - Cours

Téléchargements

Aide

En-tête

Pied de page

Appels - Exercices de programmation

Votre réponse :

Interpréteur

Editeur

Zone de saisie de texte

Une solution possible :

Interpréteur

Editeur

Votre réponse :

Interpréteur

Editeur

Zone de saisie de texte

Une solution possible :

Interpréteur

Editeur

Votre réponse :

Interpréteur

Editeur

Zone de saisie de texte

Une solution possible :

Interpréteur

Editeur

Votre réponse :

Interpréteur

Editeur

Zone de saisie de texte

Une solution possible :

Interpréteur

Editeur

Votre réponse :

Interpréteur

Editeur

Zone de saisie de texte

Une solution possible :

Interpréteur

Editeur

Votre réponse :

Interpréteur

Editeur

Zone de saisie de texte

Une solution possible :

Interpréteur

Editeur

Votre réponse :

Interpréteur

Editeur

Zone de saisie de texte

Une solution possible :

Interpréteur

Editeur

Votre réponse :

Interpréteur

Editeur

Zone de saisie de texte

Une solution possible :

Interpréteur

Editeur

Votre réponse :

Interpréteur

Editeur

Zone de saisie de texte

Une solution possible :

Interpréteur

Editeur

Votre réponse :

Interpréteur

Editeur

Zone de saisie de texte

Une solution possible :

Interpréteur

Editeur