Fichier de rejeu Close
Indication Close
A propos de... Close
Commentaire Close
Systèmes d'Information
- Notions mathématiques
- Calcul relationnel
- Algèbre relationnelle
- Langage de requêtes
- Arbre de requêtes
- QCM
- Dépendances fonctionnelles
- Décomposition de relations
- Inférence logique
- Normalisation
- Aux pays des bières
- Modélisation
- Exercices
© Your Copyright
Aide
Recherche d’information
Cette partie du cours a pour objectif de présenter la formulation générale d’une requête SQL sur une base de données relationnelles.
L’exécution d’une requête SQL correspond à la mise en œuvre d’une combinaison d’opérateurs de l’algèbre relationnelle.
Nous présenterons donc les opérateurs de l’algébre relationnelle utilisés correspondant aux requêtes proposés.
Syntaxe générale
Ecriture de requête pour rechercher de l’information
1 2 3 4 5 | SELECT [DISTINCT] <liste de colonnes>
FROM <liste de tables>
[WHERE <conditions de recherche>]
[GROUP BY <partitionnement horizontal>]
[HAVING <conditions de recherche sur les groupes>]
|
Ordre d’éxécution de la requête
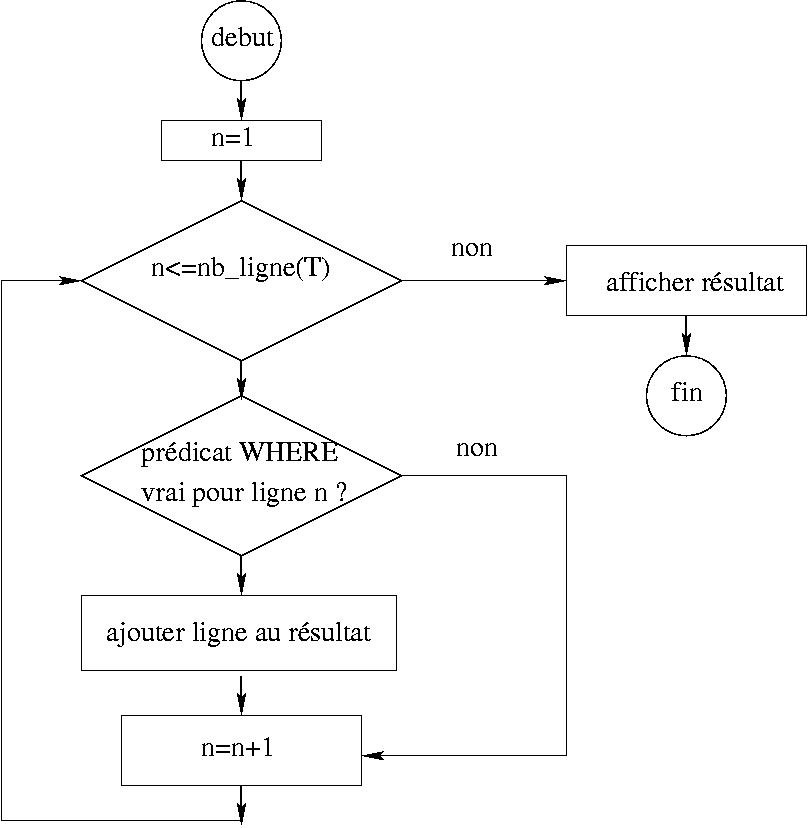
- FROM : concaténation de chaque ligne de chaque table.
- WHERE : élimination des lignes ne vérifiant pas les conditions (FALSE,UNKNOWN) sur la table de travail.
- GROUP BY : répartition des lignes résultantes dans des groupes oules valeurs dans une même colonne sont identiques
- HAVING : restriction des lignes vérifiant les conditions (TRUE) sur les regroupements.
- SELECT : élimination des colonnes non mentionnées dans SELECT
- DISTINCT : élimination des lignes dupliquées.
NB : Si GROUP BY le DISTINCT est inutile.
Recherche simple
Syntaxe générale SQL pour formuler des requêtes simples :
1 2 3 | SELECT [DISTINCT] <liste de colonnes>
FROM <liste de tables>
WHERE <conditions de recherche>
|
Ce qui revient à :
SELECT: sélectionner les informations sur certains attributs des éléments que l’on récupèreFROM: : en listant les ensembles qui contiennent les informations intéréssantesWHERE: : et en définissant une condition de restriction pour obtenir uniquement les éléments qui nous intéressent vraiment dans ces ensembles.
Ce qui correspond à la mise en œuvre des opérateurs de l’algèbre relationnelle :
- \(\large \Pi_{(a_1,...,a_n)}(S)\) : projection, opérateur unaire sur les attributs (\((a_1,...,a_n)\)) de l’ensemble \(S\).
- \(\large \times(S,T)\) : produit cartésien, opérateur binaire pour mettre en relation chaque élément de l’ensemble \(S\) avec tous les éléments de l’ensemble \(T\).
- \(\large \sigma_{[condition]}(S)\) : restriction, opérateur unaire pour définir une
conditionà satisfaire sur les éléments de l’ensemble \(S\).
Exemple :
Remarques :
Il existe des SGBD Orientés Objets (SGBDOO) proposant un langage de requêtes OQL.
La syntaxe d’une requête est très proche d’une formulation SQL :
1 2 3 | SELECT e.nom()
FROM employes e
WHERE e.ville() ='Brest'
|
Elle permet de manipuler des collections d’objets (clause FROM) et de manipuler les méthodes d’instances d’objets (clauses SELECT,WHERE).
Il y a des correspondances à faire entre la terminologie des spécialistes du « Relationnel » et ceux de l’Objet »
| Terminologie | Relationnel | Objet |
|---|---|---|
| Relation | Table | Classe |
| Attribut | Colonne | Propriété |
| Occurence | Ligne | Instance de classe |
| Domaine | Type | Type élémentaire |
| Unicité | Clé Primaire | Identité d’Objet |
| Association | Clé Etrangère | Reférence sur Classe |
Résultats de recherche
Lorsque la requête est bien formulée on peut appliquer sur le résultat :
DISTINCT: pour éliminer la redondance d’informationORDER BY: pour faire des tris sur lme résultatALL: pour éviter de faire des traitement pour éliminer de l’information
« Récupérer les différents nom des personnes «
On élimine les doublons (à éviter si possible : coût pour trier les informations)
« Trier les personnes par nom par ordre alphabétique croissant »
Trier le résultat (si nécessaire) :
- par noms de colonnes : ordre de « niveau de détails »
ASC, DESC: tri ascendant ou descendant par colonne- :code:` COLLATE` : sensible à la casse, aux accents … par colonne
« Récupérer les noms des personnes et des employés »
ALL permet d’éviter des tris pour éliminer les doublons.
Par défaut l’union (\(\cup\)) applique un tri pour éliminer les doublons.
L’exemple ci-dessous illustre l’utilisation de l’opération ensembliste d’union :
- en éliminant les doublons
- sans éliminer les doublons (
ALL)- en éliminant les doublons dans chaque ensemble (
DISTINCT) de chaque requête SQL
Opérations ensemblistes
Les opérations ensemblistes permettent de répondre à des questions du type :
- donne-moi des éléments qui se trouvent dans deux ensembles (l’union, \(\cup\))
- donne-moi des éléments qui sont commun à deux ensembles (l’intersection, \(\cap\))
- donne-moi des éléments qui se trouve dans un ensemble mais pas dans l’autre (la différence, \(\setminus\))
Ces opérations pourront aussi être exprimées par :
- des requêtes imbriquées (
IN, NOT IN, EXISTS, NOT EXISTS)- des jointures (
INNER JOIN, OUTER JOIN)
Opérations ensemblistes, jointures et SQL
\(\cup(S,T)\) : représentation en algèbre relationnelle de l’opérateur binaire d’union (\(\cup\)) entre l’ensemble \(S\) et l’ensemble \(T\)
Représentation mathématique usuelle de l’opération ensembliste : \(S \cup T\)
Exemple : « Récupérer les noms des personnes et des employes »
On veut récupérer l’ensemble des personnes et l’ensemble des employés
\(\cap(S,T)\) : représentation en algèbre relationnelle de l’opérateur binaire d’intersection (\(\cap\)) entre l’ensemble \(S\) et l’ensemble \(T\)
Représentation mathématique usuelle de l’opération ensembliste : \(S \cap T\)
Exemple : « Récupérer les noms des personnes qui sont employes »
On veut récupérer dans l’ensemble des personnes celles qui sont aussi dans l’ensemble des employés
\(\setminus(S,T)\) : représentation en algèbre relationnelle de l’opérateur binaire de différence (\(\setminus\)) entre l’ensemble \(S\) et l’ensemble \(T\)
Représentation mathématique usuelle de l’opération ensembliste : \(S \setminus T\)
Exemple : « Récupérer les noms des personnes qui ne sont pas des employes »
On veut récupérer dans l’ensemble des personnes celles qui ne sont pas dans l’ensemble des employés
Requêtes imbriquées
Les requêtes imbriquées peuvent être utilisées pour représenter des opérations ensemblistes.
L’opérateur SQL IN correspond à la relation d’appartenance mathématique (\(\in\)) à un ensemble.
L’opérateur SQL =ANY signifie que l’on teste pour chaque élément de la requête externe s’il est égal
à un des élements de la requête interne.
Exemple : « Récupérer les noms des personnes qui sont des employes »
Chaque élément de la requête externe est (appartient à) dans l’ensemble décrit par la requête imbriquée.
NB : l’opérateur =ANY n’existe pas en SQLite
L’opérateur SQL NOT IN correspond à la relation de non-appartenance mathématique (\(\neg\in\)) à un ensemble.
L’opérateur SQL <>ALL signifie que l’on teste pour chaque élément de la requête externe qu’il doit-être
différent de tous les élements de la requête interne.
Exemple : « Récupérer les noms des personnes qui ne sont pas des employes »
Chaque élément de la requête externe n’est pas (n’appartient pas à) dans l’ensemble décrit par la requête imbriquée
NB : l’opérateur <>ALL n’existe pas en SQLite
Le standard SQL propose le quantificatif existentiel (\(\exists\)) pour vérifier l’existence d’un élément dans un ensemble.
N.B : le quantificateur universel n’existe pas ( ;-) ) dans la norme SQL mais on pourra l’exprimer àl’aide d’équivalences logiques.
Exemple : « Récupérer les noms des personnes qui sont des employes »
chaque élément de la requête externe se retrouve (existe) dans l’ensemble décrit par la requête imbriquée.
Pour vérifier la non-existence (\(\neg\exists\)) d’un élément dans un ensemble.
Exemple : « Récupérer les noms des personnes qui ne sont pas des employes »
chaque élément de la requête externe ne se retrouve pas (n’existe pas) dans l’ensemble décrit par la requête imbriquée.
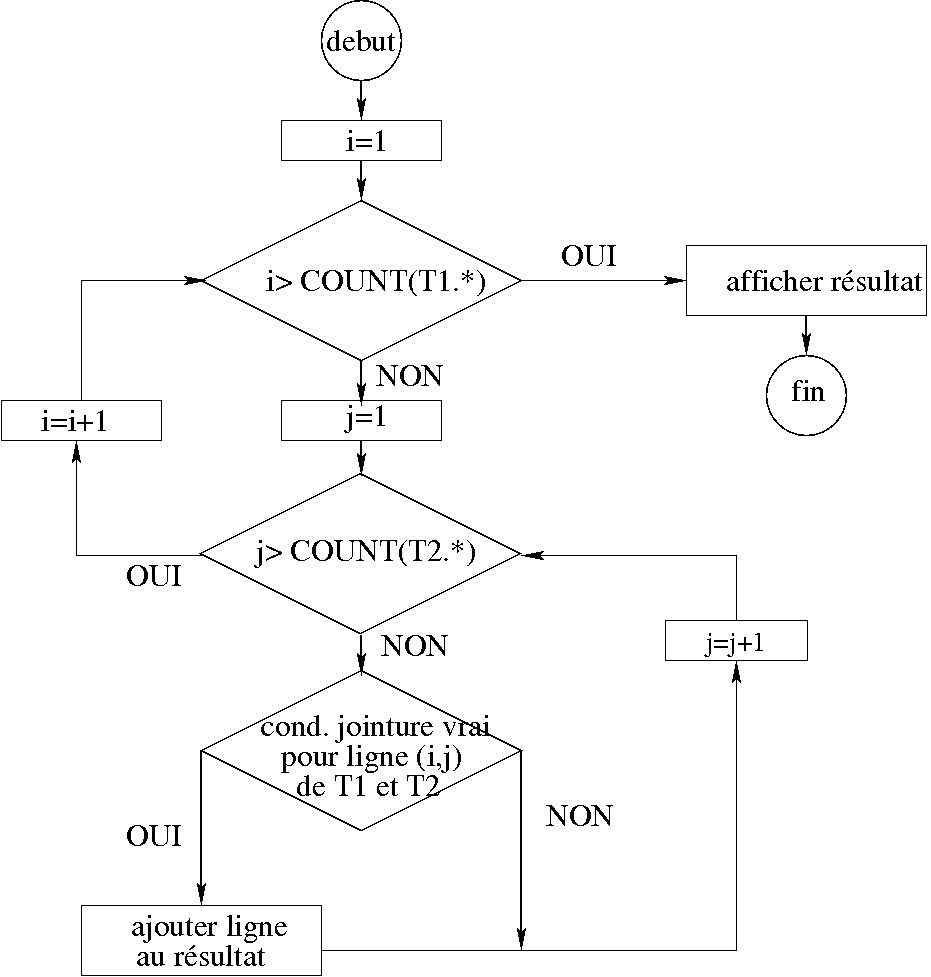
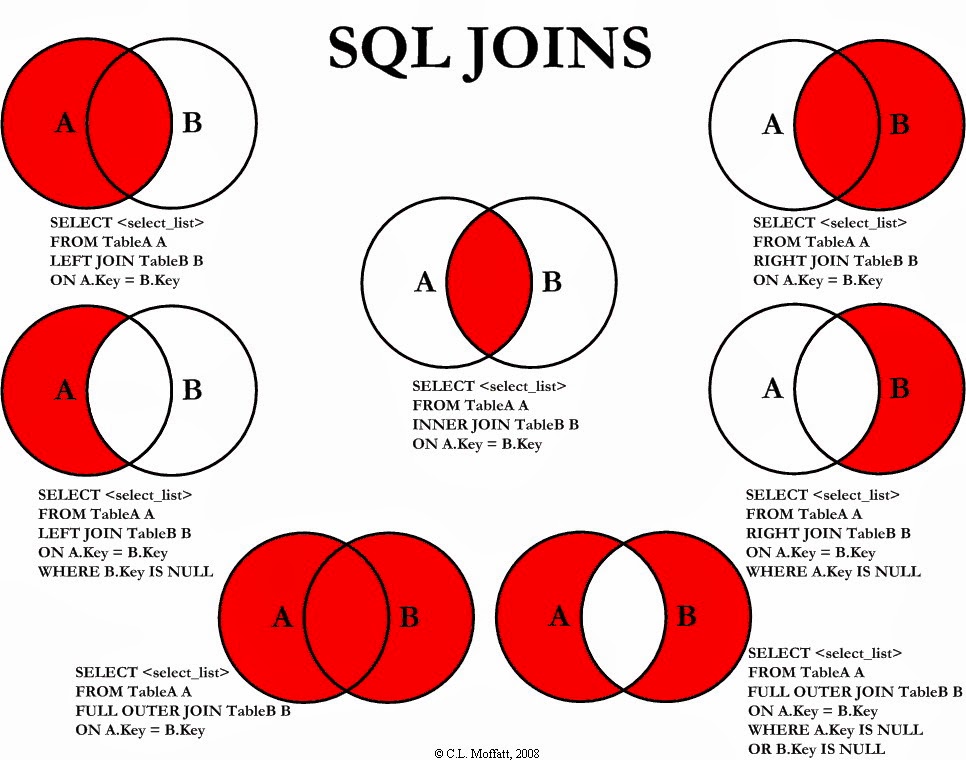
Jointures
Les jointures permettent d’associer plusieurs ensembles dans une même requête et obtenir des résultats en combinant les élements des ensembles par des critères de jointures (restriction).
Les jointures, comme les requêtes imbriquées, peuvent être utilisées pour représenter des opérations ensemblistes.
\(\times(S,T)\) : représentation en algèbre relationnelle de l’opérateur binaire du produit cartésien (\(\times\)) entre l’ensemble \(S\) et l’ensemble \(T\)
Représentation mathématique usuelle de l’opération ensembliste : \(S \times T\)
Exemple : « Récupérer toutes les combinaisons possibles de personnes et d” employes »
\(\Join_{[condition]}(S,T)\) : représentation en algèbre relationnelle de l’opérateur binaire de jointure (\(\Join\)) entre l’ensemble \(S\) et l’ensemble \(T\) avec une condition de jointure.
La jointure interne consiste à ne retenir dans le résultat que les éléments qui satisferont la condition de jointure.
\(\sigma_{[condition]}(\times(S,T))\) : la jointure interne est une combinaison d’opérateurs de base (\(\times,\sigma\)) de l’algèbre relationnelle.
Exemple : « Récupérer les noms des personnes qui sont des employes »
« Récupérer les noms des personnes qui seraient éventuellement des employés »
La restriction permet de retenir dans le résultat les élements sur lesquels on ne peut vérifier la condition (UNKNOWN)
- LEFT : propositions invérifiables à gauche de l’opérateur logique
- RIGHT : propositions invérifiables à droite de l’opérateur logique
- FULL : propositions invérifiables des dexu côtés de l’opérateur logique
\(\Join(S,T)\) : représentation en algèbre relationnelle de l’opérateur binaire de jointure naturelle (\(\Join\)) entre l’ensemble \(S\) et l’ensemble \(T\).
La condition de jointure se fera naturellement sur les colonnes de même nom communes aux deux ensembles et définies sur le même domaine de valeurs
Fonctions d’agrégats
- Les fonctions d’agrégats sont des fonctions SQL qui permettrons d’appliquer des calculs sur :
- l’ensemble résultat des requêtes SQL
- les requêtes imbriquées
- les sous-ensembles obtenus par groupement
« donner le nombre de personnes enregistrés dans la base de données »
Obtenir le nombre d’occurences
« Quelle est la moyenne d’âge des personnes enregistrés dans la base de données »
sql : essai.sqlOutput
« Quel est l’écart-type de l’âge des personnes enregistrés dans la base de données »
sql : essai.sqlOutputCommentairesLes fonctions stddev ne sont pas implémentées dans cette version de SQLite.
« variance de l’âge des personnes enregistrés dans la base de données »
sql : essai.sqlOutput
« personnes dont l’âge est supérieur à la moyenne «
sql : essai.sqlOutput
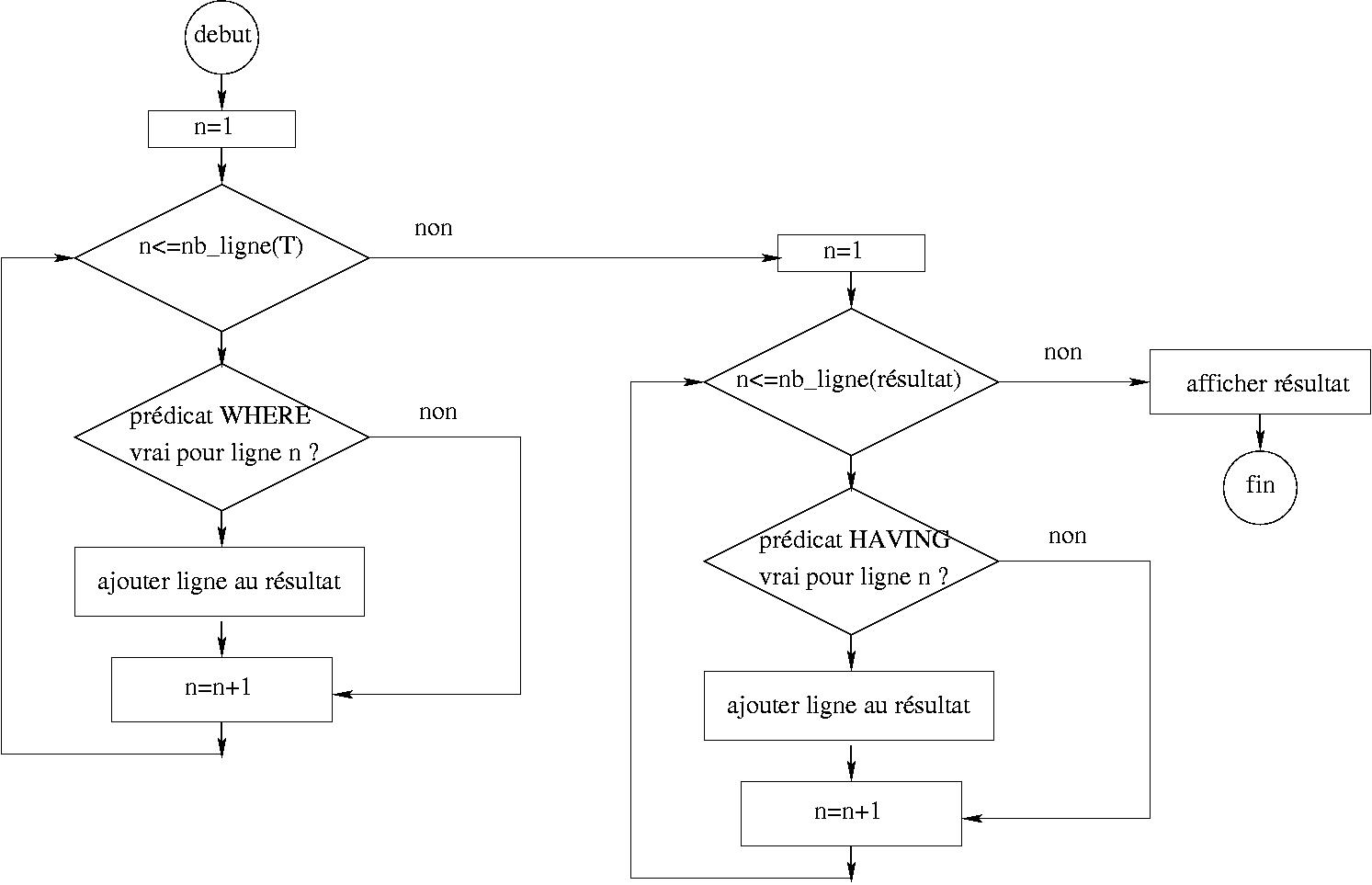
Groupement
« donner, par âge, le nombre de personnes »
Regrouper des éléments dans des sous-ensembles
sql : essai.sqlOutput
« donner, par âge, le nombre de personnes s’ils sont au moins 2
Faire des restrictions sur les groupements
sql : essai.sqlOutput
« donner, par âge, pour les personnes de moins de 25 ans le nombre de personnes s’ils sont au moins 2 »
Faire des restrictions sur l’ensemble et sur les groupements dans l’ensemble
sql : essai.sqlOutput
Exécution de requêtes
D’un point de vue programmation, le traitement des requêtes SQL peut être représentée par des boucles simples ou imbriquées avec alternatives .
boucle de parcours des élements de T avec test sur la clause WHERE
boucles imbriquées pour parcourir les élements de T1,T2 … avec tests sur critères de jointure
boucles successives pour parcourir les groupements sur la clause HAVING
SQL et les mathématiques
On peut établir une correspondance entre des éléments de mathématiques (ensembles, logique) et les requêtes SQL.
Pour établir correctement une requête SQL, il est nécessaire d’avoir une représentation du problème en terme de manipulation d’ensembles
et de formulation logique de question à poser sur une base de données relationnelles.
| Notion | Maths | SQL |
|---|---|---|
| appartenance | \(\in\) | IN |
| négation | \(\neg\) | NOT |
| existence | \(\exists\) | EXISTS |
| union | \(\cup\) | UNION |
| intersection | \(\cap\) | INTERSECT |
| différence | \(\displaystyle {\backslash}\) | EXCEPT |
| ET logique | \(\land\) | AND |
| OU logique | \(\lor\) | OR |
- Lien wikipedia sur des notions de Logique, table de vérités, diagrammes de Venn … utile à la compréhension de requêtes
- SQL