Fichier de rejeu Close
Indication Close
A propos de... Close
Commentaire Close
Aide
Définition de fonction
Ce chapitre propose de tester les acquis d'apprentissage concernant les notions de fonction et de procédure, objets essentiels à la structuration et à la réutilisation des algorithmes.
Plus particulièrement, elle s'intéresse à la définition des fonctions à travers leur spécification (ie. que fait la fonction ?) et leur implémentation (ie. comment fait la fonction ?).
Deux types de tests sont proposés :
- un test de compréhension d'une durée indicative de 30',
- un test de programmation d'une durée indicative de 60'.
Test de programmation
-
1/17 Appliquer 1
-
Circuit logique
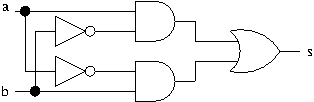
Définir (spécification + implémentation) une fonction qui calcule la sortie du circuit logique ci-dessous en fonction de ses entrées.
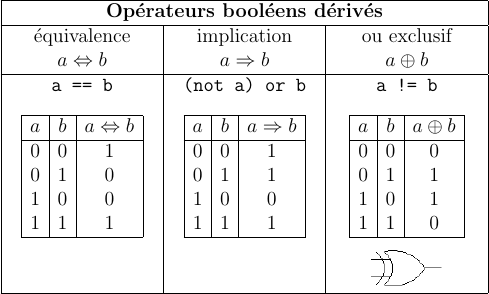
 opérateurs booléens
opérateurs booléens

Votre réponse :
AAV4_DEF: Résultat
Utiliser l'interpréteur Python ci-dessous pour programmer l'algorithme demandé.
python : essai.pyOutputAAV4_DEF: Vérification
Appliquer cette technique au résultat proposé.
Si cette technique nécessite d'être implémentée en Python, le faire dans l'interpréteur Python ci-dessus (cf. Résultat), sinon développer la technique de vérification dans l'éditeur de texte ci-dessous.
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie
Une solution possible :
AAV4_DEF: Répondre explicitement à la question posée
La définition attendue est présentée ci-dessous.
python : fonction-type-boolean.pyOutputAAV4_DEF: Choisir et appliquer une technique de vérification
La vérification par jeu de tests est mise en œuvre : la fonction définie précédemment est conforme au jeu de tests.
Le circuit implante bien le « ou exclusif ».
-
Le plus grand des 3 nombres
Définir (spécification + implémentation) une fonction qui détermine le plus grand des trois nombres \(x_1\), \(x_2\) et \(x_3\).
Votre réponse :
AAV4_DEF: Résultat
Utiliser l'interpréteur Python ci-dessous pour programmer l'algorithme demandé.
python : essai.pyOutputAAV4_DEF: Vérification
Appliquer cette technique au résultat proposé.
Si cette technique nécessite d'être implémentée en Python, le faire dans l'interpréteur Python ci-dessus (cf. Résultat), sinon développer la technique de vérification dans l'éditeur de texte ci-dessous.
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie
Une solution possible :
AAV4_DEF: Répondre explicitement à la question posée
La définition attendue est présentée ci-dessous.
python : fonction-type-number.pyOutputAAV4_DEF: Choisir et appliquer une technique de vérification
La vérification par jeu de tests est mise en œuvre : la fonction définie précédemment est conforme au jeu de tests.
-
Codage en base b
Définir (spécification + implémentation) une fonction qui code un entier décimal \(n\) en base \(b\). Le nombre binaire sera codé sous forme d'une liste d'entiers composée des chiffres de la base \(b\).
Numération en base bUn entier \(n\) en base \(b\) est représenté par une suite de chiffres \((r_mr_{m-1}\ldots r_1r_0)_b\) où les \(r_i\) sont des chiffres de la base \(b\) (\(0\leq r_i < b\)). Ce nombre \(n\) a pour valeur :
\[n = r_mb^m + r_{m-1}b^{m-1} + \ldots + r_1b^1 + r_0b^0 = \sum^{i=m}_{i = 0} r_ib^i\]L'algorithme de conversion en base \(b\) consiste à diviser successivement le nombre \(n\) par la base \(b\) (\(n = bq + r\)) tant que le quotient \(q\) n'est pas nul. L'ordre inverse des restes \(r_i\) des différentes divisions (du dernier au premier reste, écrits de gauche à droite) donne la représentation du nombre \(n\) en base \(b\).
\[\begin{array}{lll} n &=& q_0b + r_0 = q_0b^1 + {r_0b^0}\\ n &=& (q_1b^1 + r_1)b^1 + r_0b^0 = q_1b^2 + {r_1b^1 + r_0b^0} \\ n &=& (q_2b^1 + r_2)b^2 + r_1b^1 + r_0b^0 = q_2b^3 + {r_2b^2 + r_1b^1 + r_0b^0}\\ n &=& \ldots\\ n &=& 0\cdot b^{m+1} + {r_mb^m + \ldots + r_2b^2 + r_1b^1 + r_0b^0} = \displaystyle \sum^{i=m}_{i = 0} r_ib^i\\ n &=& (r_mr_{m-1}\ldots r_1r_0)_b \end{array}\]Votre réponse :
AAV4_DEF: Résultat
Utiliser l'interpréteur Python ci-dessous pour programmer l'algorithme demandé.
python : essai.pyOutputAAV4_DEF: Vérification
Appliquer cette technique au résultat proposé.
Si cette technique nécessite d'être implémentée en Python, le faire dans l'interpréteur Python ci-dessus (cf. Résultat), sinon développer la technique de vérification dans l'éditeur de texte ci-dessous.
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie
Une solution possible :
AAV4_DEF: Répondre explicitement à la question posée
La définition attendue est présentée ci-dessous.
python : fonction-type-number-2.pyOutputAAV4_DEF: Choisir et appliquer une technique de vérification
La vérification par jeu de tests est mise en œuvre : la fonction définie précédemment est conforme au jeu de tests.
-
Palindrome
Définir (spécification + implémentation) une fonction qui teste si une séquence (
str,tupleoulist) est un palindrome.Votre réponse :
AAV4_DEF: Résultat
Utiliser l'interpréteur Python ci-dessous pour programmer l'algorithme demandé.
python : essai.pyOutputAAV4_DEF: Vérification
Appliquer cette technique au résultat proposé.
Si cette technique nécessite d'être implémentée en Python, le faire dans l'interpréteur Python ci-dessus (cf. Résultat), sinon développer la technique de vérification dans l'éditeur de texte ci-dessous.
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie
Une solution possible :
AAV4_DEF: Répondre explicitement à la question posée
La définition attendue est présentée ci-dessous.
python : fonction-type-tuple.pyOutputAAV4_DEF: Choisir et appliquer une technique de vérification
La vérification par jeu de tests est mise en œuvre : la fonction définie précédemment est conforme au jeu de tests.
-
Recherche d'un élément
Définir (spécification + implémentation) une fonction qui détermine le rang de la première occurence d'un élément au sein d'une séquence (str, tuple ou list).
Votre réponse :
AAV4_DEF: Résultat
Utiliser l'interpréteur Python ci-dessous pour programmer l'algorithme demandé.
python : essai.pyOutputAAV4_DEF: Vérification
Appliquer cette technique au résultat proposé.
Si cette technique nécessite d'être implémentée en Python, le faire dans l'interpréteur Python ci-dessus (cf. Résultat), sinon développer la technique de vérification dans l'éditeur de texte ci-dessous.
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie
Une solution possible :
AAV4_DEF: Répondre explicitement à la question posée
La définition attendue est présentée ci-dessous.
python : fonction-type-list.pyOutputAAV4_DEF: Choisir et appliquer une technique de vérification
La vérification par jeu de tests est mise en œuvre : la fonction définie précédemment est conforme au jeu de tests.
-
Spirales rectangulaires
Définir (spécification + implémentation) une fonction qui trace avec la tortue Logo une spirale rectangulaire de \(n\) côtés à partir du point \(A(x_A,y_A)\) et dont le côté initial fait un angle \(\theta\) avec l'axe des \(x\). La longueur du côté initial de la spirale est \(d_0\) et l'accroissement algébrique d'un côté à l'autre est \(dx\).
 aide Python
aide Pythontortue Logo : (documentation Python)
import turtlemodule Python à importer pour manipuler la tortue Logo.
t = turtle.Turtle()crée une tortue
t.t.setheading(a)oriente la tortue
tdans une direction qui fait l'anglea(en degrés) avec l'axe horizontal (sens trigonométrique).t.forward(d)fait avancer la tortue
td'une distanceddans la direction courante.t.backward(d)fait reculer la tortue
td'une distanceddans la direction courante.t.left(a)fait tourner sur la gauche (sens trigonométrique) la tortue
t(sans avancer, ni reculer) d'un angleapar rapport à la direction courante.t.right(a)fait tourner sur la droite (sens horaire) la tortue
t(sans avancer, ni reculer) d'un angleapar rapport à la direction courante.t.goto(x,y)fait aller la tortue au point de coordonnées
(x,y)quelle que soit son orientation.Votre réponse :
AAV4_DEF: Résultat
Utiliser l'interpréteur Python ci-dessous pour programmer l'algorithme demandé.
python : essai.pyOutputAAV4_DEF: Vérification
Appliquer cette technique au résultat proposé.
Si cette technique nécessite d'être implémentée en Python, le faire dans l'interpréteur Python ci-dessus (cf. Résultat), sinon développer la technique de vérification dans l'éditeur de texte ci-dessous.
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie
Une solution possible :
AAV4_DEF: Répondre explicitement à la question posée
Le code Python du tracé d'une spirale rectangulaire est donné ci-dessous.
python : fonction-logo-2.pyOutputAAV4_DEF: Choisir et appliquer une technique de vérification
La vérification par jeu de tests est mise en œuvre : la fonction définie précédemment est conforme au jeu de tests.
-
Polygone régulier
Définir (spécification + implémentation) une fonction qui trace avec la tortue Logo un polygone régulier de \(n\) côtés de longueur \(d\) à partir du point \(A(x_A,y_A)\), le premier côté faisant un angle \(\theta\) avec l'axe des \(x\).
aide Pythontortue Logo : (documentation Python)
import turtlemodule Python à importer pour manipuler la tortue Logo.
t = turtle.Turtle()crée une tortue
t.t.setheading(a)oriente la tortue
tdans une direction qui fait l'anglea(en degrés) avec l'axe horizontal (sens trigonométrique).t.forward(d)fait avancer la tortue
td'une distanceddans la direction courante.t.backward(d)fait reculer la tortue
td'une distanceddans la direction courante.t.left(a)fait tourner sur la gauche (sens trigonométrique) la tortue
t(sans avancer, ni reculer) d'un angleapar rapport à la direction courante.t.right(a)fait tourner sur la droite (sens horaire) la tortue
t(sans avancer, ni reculer) d'un angleapar rapport à la direction courante.t.goto(x,y)fait aller la tortue au point de coordonnées
(x,y)quelle que soit son orientation.Votre réponse :
AAV4_DEF: Résultat
Utiliser l'interpréteur Python ci-dessous pour programmer l'algorithme demandé.
python : essai.pyOutputAAV4_DEF: Vérification
Appliquer cette technique au résultat proposé.
Si cette technique nécessite d'être implémentée en Python, le faire dans l'interpréteur Python ci-dessus (cf. Résultat), sinon développer la technique de vérification dans l'éditeur de texte ci-dessous.
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie
Une solution possible :
AAV4_DEF: Répondre explicitement à la question posée
Le code Python du tracé d'un polygone régulier est donné ci-dessous.
python : fonction-logo-3.pyOutputAAV4_DEF: Choisir et appliquer une technique de vérification
La vérification par jeu de tests est mise en œuvre : la fonction définie précédemment est conforme au jeu de tests.
-
Dilemme du prisonnier
Deux suspects sont arrêtés par la police. Mais les inspecteurs n'ont pas assez de preuves pour les inculper. Ils les interrogent alors séparément en leur faisant la même offre :
- Si tu dénonces ton complice et qu'il ne te dénonce pas, tu seras remis en liberté et il écopera de la peine maximale.
- Si tu le dénonces et qu'il te dénonce aussi, vous écoperez tous les deux de la moitié de la peine maximale.
- Si personne ne se dénonce, vous écoperez tous les deux de la peine minimale.
Ce dilemme se résume dans le tableau suivant où chaque case représente la peine obtenue selon le comportement des 2 suspects. Ainsi par exemple \((0;max)\) signifie que le suspect 1 sera libéré et le suspect 2 aura la peine maximale, \((max;0)\) que le suspect 1 écopera de la peine maximale et le suspect 2 sera libéré...
2 se tait 2 dénonce 1 1 se tait \((min;min)\) \((max;0)\) 1 dénonce 2 \((0;max)\) \((max/2;max/2)\) Définir (spécification + implémentation) une fonction qui détermine la peine encourue par chacun des 2 suspects en fonction de leur comportement.
Votre réponse :
AAV4_DEF: Résultat
Utiliser l'interpréteur Python ci-dessous pour programmer l'algorithme demandé.
python : essai.pyOutputAAV4_DEF: Vérification
Appliquer cette technique au résultat proposé.
Si cette technique nécessite d'être implémentée en Python, le faire dans l'interpréteur Python ci-dessus (cf. Résultat), sinon développer la technique de vérification dans l'éditeur de texte ci-dessous.
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie
Une solution possible :
AAV4_DEF: Répondre explicitement à la question posée
Le code Python du dilemme du prisonnier est donné ci-dessous.
python : fonction-jeux-1.pyOutputAAV4_DEF: Choisir et appliquer une technique de vérification
La vérification par jeu de tests est mise en œuvre : la fonction définie précédemment est conforme au jeu de tests.
-
Distribuer les cartes
Définir (spécification + implémentation) une fonction qui distribue aléatoirement un jeu de \(n\) cartes à tour de rôle entre \(r\) joueurs de telle manière que chaque joueur reçoive le même nombre de cartes. Les \((n\mod r)\) cartes non distribuées sont mises dans une pioche.
Votre réponse :
AAV4_DEF: Résultat
Utiliser l'interpréteur Python ci-dessous pour programmer l'algorithme demandé.
python : essai.pyOutputAAV4_DEF: Vérification
Appliquer cette technique au résultat proposé.
Si cette technique nécessite d'être implémentée en Python, le faire dans l'interpréteur Python ci-dessus (cf. Résultat), sinon développer la technique de vérification dans l'éditeur de texte ci-dessous.
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie
Une solution possible :
AAV4_DEF: Répondre explicitement à la question posée
Le code Python de distribution des cartes est donné ci-dessous.
python : fonction-jeux-2.pyOutputAAV4_DEF: Choisir et appliquer une technique de vérification
La vérification par jeu de tests est mise en œuvre : la fonction définie précédemment est conforme au jeu de tests.
Par ailleurs, on vérifie « à la main » que la fonction est également conforme aux règles du jeu :
- les cartes sont toutes différentes les unes des autres;
- les joueurs ont le même nombre de cartes;
- la pioche contient \((n\mod r)\) cartes.
-
Classer par couleurs
On ne s'intéresse ici qu'à la couleur d'une carte (pique=0, cœur=1, carreau=2, trèfle=3), pas à sa valeur (1, 2, 3, ..., 10, V, D, R).
On considère une « main » de \(n\) cartes distribuées aléatoirement. Une main sera représentée par une liste de couleurs.
Exemples de mains à 7 cartes:
[2, 0, 3, 2, 1, 2, 0] [0, 3, 1, 3, 1, 1, 0] [2, 1, 0, 2, 3, 3, 2] [2, 2, 3, 2, 2, 1, 3]
Définir (spécification + implémentation) une fonction qui classe les cartes d'une « main » par couleurs : tous les piques en premier, tous les cœurs en deuxième, puis les carreaux et enfin les trèfles.
Exemples d'ordonnancements pour des mains à 7 cartes:
avant : [2, 0, 3, 2, 1, 2, 0] après : [0, 0, 1, 2, 2, 2, 3] avant : [0, 3, 1, 3, 1, 1, 0] après : [0, 0, 1, 1, 1, 3, 3] avant : [3, 3, 0, 3, 0, 1, 0] après : [0, 0, 0, 1, 3, 3, 3] avant : [1, 1, 1, 1, 1, 1, 1] après : [1, 1, 1, 1, 1, 1, 1] avant : [3, 3, 2, 2, 2, 1, 0] après : [0, 1, 2, 2, 2, 3, 3] avant : [1, 2, 2, 2, 2, 3, 3] après : [1, 2, 2, 2, 2, 3, 3]
Votre réponse :
AAV4_DEF: Résultat
Utiliser l'interpréteur Python ci-dessous pour programmer l'algorithme demandé.
python : essai.pyOutputAAV4_DEF: Vérification
Appliquer cette technique au résultat proposé.
Si cette technique nécessite d'être implémentée en Python, le faire dans l'interpréteur Python ci-dessus (cf. Résultat), sinon développer la technique de vérification dans l'éditeur de texte ci-dessous.
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie
Une solution possible :
AAV4_DEF: Répondre explicitement à la question posée
Le code Python du classement par couleur est donné ci-dessous.
python : fonction-jeux-3.pyOutputAAV4_DEF: Choisir et appliquer une technique de vérification
La vérification par jeu de tests est mise en œuvre : la fonction définie précédemment est conforme au jeu de tests.
- On vérifie en particulier
- que la « main » est bien triée par couleurs (indépendamment des valeurs des cartes au sein d'une même couleur);
- que différents types de « main » : 1 seule couleur, plusieurs couleurs non classées, plusieurs couleurs déjà classées, plusieurs couleurs classées en ordre inverse... sont correctement triées;
- que les résultats obtenus avec la fonction proposée
classer(main)sont identiques aux résultats de la méthodemain.sort()de la bibliothèque Python.
-
Mentions au bac
Définir (spécification + implémentation) une fonction qui détermine la mention au bac (ajourné, passable, assez bien, bien ou très bien) en fonction de la moyenne générale \(n\) obtenue par un bachelier.
Votre réponse :
AAV4_DEF: Résultat
Utiliser l'interpréteur Python ci-dessous pour programmer l'algorithme demandé.
python : essai.pyOutputAAV4_DEF: Vérification
Appliquer cette technique au résultat proposé.
Si cette technique nécessite d'être implémentée en Python, le faire dans l'interpréteur Python ci-dessus (cf. Résultat), sinon développer la technique de vérification dans l'éditeur de texte ci-dessous.
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie
Une solution possible :
AAV4_DEF: Répondre explicitement à la question posée
Le code Python de la mention au bac est présenté ci-dessous.
python : fonction-elem-3.pyOutputAAV4_DEF: Choisir et appliquer une technique de vérification
La vérification par jeu de tests est mise en œuvre : la fonction définie précédemment est conforme au jeu de tests.
-
Suite arithmétique
Définir (spécification + implémentation) une fonction qui calcule la somme \(s\) des \(n+1\) premiers termes \(u_k\) d'une suite arithmétique de premier terme \(u_0\) et de raison \(r\) : \(u_k = u_0 + kr\).
rappels mathématiquesLa somme arithmétique \(S = (1+2+\ldots\ +n)\) des \(n+1\) premiers entiers est telle que :
\(\begin{array}{rrccccccccccccc} & S &=& 1 &+& 2 &+& 3 &+& \ldots &+& (n-1) &+& n \\ + & S &=& n &+& (n-1) &+& (n-2) &+& \ldots &+& 2 &+& 1 \\ = & 2S &=& (n+1) &+& (n+1) &+& (n+1) &+& \ldots &+& (n+1) &+& (n+1)\\ \end{array}\)
On en déduit : \(S = \displaystyle\frac{n(n+1)}{2}\).
La somme géométrique \(S = (1 + q + q^2 + \ldots\ + q^n)\) de raison \(q \neq 1\) est telle que :
\(\begin{array}{rcccccccccccccc} S &=& 1 &+& q &+& q^2 &+& \ldots &+& q^{(n-1)} &+& q^n & & \\ qS &=& & & q &+& q^2 &+& \ldots &+& q^{(n-1)} &+& q^n &+& q^{(n+1)} \\ (1-q)S &=& 1 &+& 0 &+& 0 &+& \ldots &+& 0 &+& 0 &-& q^{(n+1)} \\ \end{array}\)
On en déduit : \(S = \displaystyle\frac{1-q^{(n+1)}}{1-q}\).
Votre réponse :
AAV4_DEF: Résultat
Utiliser l'interpréteur Python ci-dessous pour programmer l'algorithme demandé.
python : essai.pyOutputAAV4_DEF: Vérification
Appliquer cette technique au résultat proposé.
Si cette technique nécessite d'être implémentée en Python, le faire dans l'interpréteur Python ci-dessus (cf. Résultat), sinon développer la technique de vérification dans l'éditeur de texte ci-dessous.
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie
Une solution possible :
AAV4_DEF: Répondre explicitement à la question posée
La définition attendue est présentée dans l'interpréteur ci-dessous.
python : fonction-prop-1.pyOutputAAV4_DEF: Choisir et appliquer une technique de vérification
La vérification par jeu de tests est mise en œuvre : la fonction définie précédemment est conforme au jeu de tests.
-
Suite géométrique
Définir (spécification + implémentation) une fonction qui calcule la somme \(s\) des \(n+1\) premiers termes \(u_k\) d'une suite géométrique de premier terme \(u_0\) et de raison \(q\) : \(u_k = u_0\cdot q^k\).
rappels mathématiquesLa somme arithmétique \(S = (1+2+\ldots\ +n)\) des \(n+1\) premiers entiers est telle que :
\(\begin{array}{rrccccccccccccc} & S &=& 1 &+& 2 &+& 3 &+& \ldots &+& (n-1) &+& n \\ + & S &=& n &+& (n-1) &+& (n-2) &+& \ldots &+& 2 &+& 1 \\ = & 2S &=& (n+1) &+& (n+1) &+& (n+1) &+& \ldots &+& (n+1) &+& (n+1)\\ \end{array}\)
On en déduit : \(S = \displaystyle\frac{n(n+1)}{2}\).
La somme géométrique \(S = (1 + q + q^2 + \ldots\ + q^n)\) de raison \(q \neq 1\) est telle que :
\(\begin{array}{rcccccccccccccc} S &=& 1 &+& q &+& q^2 &+& \ldots &+& q^{(n-1)} &+& q^n & & \\ qS &=& & & q &+& q^2 &+& \ldots &+& q^{(n-1)} &+& q^n &+& q^{(n+1)} \\ (1-q)S &=& 1 &+& 0 &+& 0 &+& \ldots &+& 0 &+& 0 &-& q^{(n+1)} \\ \end{array}\)
On en déduit : \(S = \displaystyle\frac{1-q^{(n+1)}}{1-q}\).
Votre réponse :
AAV4_DEF: Résultat
Utiliser l'interpréteur Python ci-dessous pour programmer l'algorithme demandé.
python : essai.pyOutputAAV4_DEF: Vérification
Appliquer cette technique au résultat proposé.
Si cette technique nécessite d'être implémentée en Python, le faire dans l'interpréteur Python ci-dessus (cf. Résultat), sinon développer la technique de vérification dans l'éditeur de texte ci-dessous.
Texte : inputlines448.txtZone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie
Une solution possible :
AAV4_DEF: Répondre explicitement à la question posée
La définition attendue est présentée dans l'interpréteur ci-dessous.
python : fonction-prop-2.pyOutputAAV4_DEF: Choisir et appliquer une technique de vérification
La vérification par jeu de tests est mise en œuvre : la fonction définie précédemment est conforme au jeu de tests.
-
Graphe de fonction
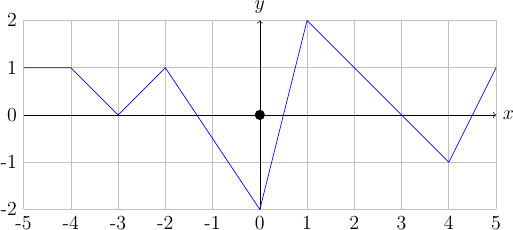
Définir (spécification + implémentation) une fonction qui calcule la fonction \(y = f(x)\) définie sur \([-5;5]\) par le graphe ci-dessous et \(\forall x < -5, f(x) = f(-5)\) et \(\forall x > 5, f(x) = f(5)\).
Votre réponse :
AAV4_DEF: Résultat
Utiliser l'interpréteur Python ci-dessous pour programmer l'algorithme demandé.
python : essai.pyOutputAAV4_DEF: Vérification
Appliquer cette technique au résultat proposé.
Si cette technique nécessite d'être implémentée en Python, le faire dans l'interpréteur Python ci-dessus (cf. Résultat), sinon développer la technique de vérification dans l'éditeur de texte ci-dessous.
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie
Une solution possible :
AAV4_DEF: Répondre explicitement à la question posée
La définition attendue est présentée dans l'interpréteur ci-dessous.
python : fonction-prop-3.pyOutputAAV4_DEF: Choisir et appliquer une technique de vérification
La vérification par jeu de tests est mise en œuvre : la fonction définie précédemment est conforme au jeu de tests.
-
Racines du trinome
Définir (spécification + implémentation) une fonction qui détermine la liste des racines réelles d'un trinôme \(ax^2 + bx + c\) à coefficients réels.
aide Python- Module random
Ce module permet de générer des nombres pseudo-aléatoires.
Exemple:
import random n = random.randint(0,100) e = random.choice([1,2,3,4,5,6]) p = random.random()
- Fonctions :
choice, randint, random, randrange, seed, shuffle, uniform
- Documentation officielle :
- Module math
Ce module permet de manipuler les principales fonctions mathématiques.
Exemple:
import math pi = math.pi y = math.log(math.sin(math.pi/2))
- Constantes :
pi, e
- Fonctions :
acos, acosh, asin, asinh, atan, atan2, atanh, ceil, copysign, cos, cosh, degrees, exp, fabs, factorial, floor, hypot, isnan, log, log10, pow, radians, sin, sinh, sqrt, tan, tanh, trunc
- Documentation officielle :
Votre réponse :
AAV4_DEF: Résultat
Utiliser l'interpréteur Python ci-dessous pour programmer l'algorithme demandé.
python : essai.pyOutputAAV4_DEF: Vérification
Appliquer cette technique au résultat proposé.
Si cette technique nécessite d'être implémentée en Python, le faire dans l'interpréteur Python ci-dessus (cf. Résultat), sinon développer la technique de vérification dans l'éditeur de texte ci-dessous.
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie
Une solution possible :
AAV4_DEF: Répondre explicitement à la question posée
La définition attendue est présentée dans l'interpréteur ci-dessous.
python : fonction-prop-4.pyOutputAAV4_DEF: Choisir et appliquer une technique de vérification
La vérification par jeu de tests est mise en œuvre : la fonction définie précédemment est conforme au jeu de tests.
-
Intégration numérique
Soit \(f(x)\) une fonction continue de \(R \rightarrow R\) à intégrer sur \([a,b]\). On supposera que \(f\) à toutes les bonnes propriétés mathématiques pour être intégrable sur l'intervalle considéré.
On cherche à calculer son intégrale \(\displaystyle I = \int_a^b f(x)dx\) qui représente classiquement l'aire comprise entre la courbe représentative de \(f\) et les droites d'équations \(x=a\), \(x=b\) et \(y=0\). Les principales méthodes d'intégration numérique consistent essentiellement à trouver une bonne approximation de cette aire.
Dans la méthode des rectangles, on subdivise l'intervalle d'intégration de longueur \(b-a\) en \(n\) parties égales de longueur \(\displaystyle\Delta x = \frac{b-a}{n}\).
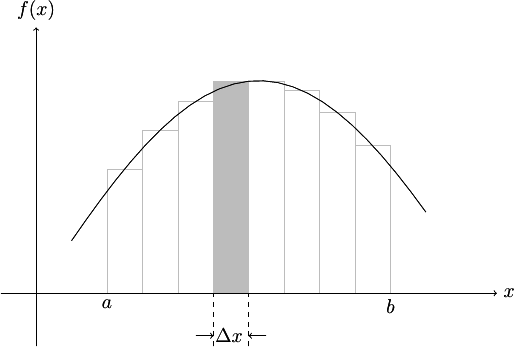
Soient \(x_1\), \(x_2\), ..., \(x_n\) les points milieux de ces \(n\) intervalles. Les \(n\) rectangles formés avec les ordonnées correspondantes ont pour surface \(f(x_1)\Delta x\), \(f(x_2)\Delta x\), ..., \(f(x_n)\Delta x\). L'aire sous la courbe est alors assimilée à la somme des aires de ces rectangles, soit :
\(\displaystyle I = \int_a^b f(x)dx \approx \left(f(x_1)+f(x_2)+\cdots+f(x_n)\right)\Delta x\)
C'est la formule dite des rectangles qui repose sur une approximation par une fonction en escalier.
Définir (spécification + implémentation) une fonction qui l'intégrale d'une fonction \(f(x)\) sur \([a,b]\) à l'ordre \(n\) par la méthode des rectangles.
aide Python- Module random
Ce module permet de générer des nombres pseudo-aléatoires.
Exemple:
import random n = random.randint(0,100) e = random.choice([1,2,3,4,5,6]) p = random.random()
- Fonctions :
choice, randint, random, randrange, seed, shuffle, uniform
- Documentation officielle :
- Module math
Ce module permet de manipuler les principales fonctions mathématiques.
Exemple:
import math pi = math.pi y = math.log(math.sin(math.pi/2))
- Constantes :
pi, e
- Fonctions :
acos, acosh, asin, asinh, atan, atan2, atanh, ceil, copysign, cos, cosh, degrees, exp, fabs, factorial, floor, hypot, isnan, log, log10, pow, radians, sin, sinh, sqrt, tan, tanh, trunc
- Documentation officielle :
Votre réponse :
AAV4_DEF: Résultat
Utiliser l'interpréteur Python ci-dessous pour programmer l'algorithme demandé.
python : essai.pyOutputAAV4_DEF: Vérification
Appliquer cette technique au résultat proposé.
Si cette technique nécessite d'être implémentée en Python, le faire dans l'interpréteur Python ci-dessus (cf. Résultat), sinon développer la technique de vérification dans l'éditeur de texte ci-dessous.
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie
Une solution possible :
AAV4_DEF: Répondre explicitement à la question posée
La définition attendue est présentée dans l'interpréteur ci-dessous.
python : fonction-prop-5.pyOutputAAV4_DEF: Choisir et appliquer une technique de vérification
La vérification par jeu de tests est mise en œuvre : la fonction définie précédemment est conforme au jeu de tests.
-
Zéro d'une fonction
On recherche le zéro d'une fonction \(f\) continue sur un intervalle \([a,b]\) telle que \(f(a).f(b) < 0\); il existe donc une racine de \(f\) dans \(]a,b[\) que l'on supposera unique.
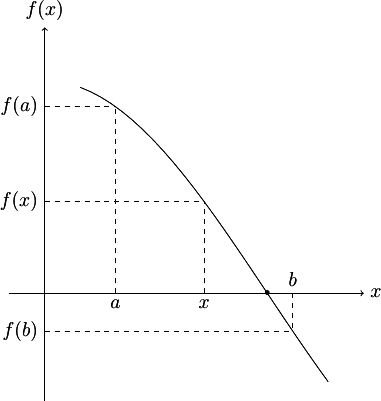
Les principales méthodes de recherche du zéro d'une fonction reposent sur une méthode par dichotomie. On sépare l'espace de recherche de la solution (ici l'intervalle \([a,b]\)) en 2 sous-espaces disjoints et, si on dispose d'un critère pour déterminer le sous-espace qui contient la solution recherchée (ici la condition \(f(a).f(b) < 0\)), on réitère la méthode sur le sous-espace candidat. A chaque étape, l'espace de recherche est ainsi divisé en 2 sous-espaces plus petits. Lorsque le sous-espace restant est considéré comme suffisamment petit, on estime avoir trouvé la solution (ici le zéro de la fonction).
Ici, notre critère de division de l'intervalle de recherche \([a,b]\) sera de le partager en deux par son milieu. Ainsi, on pose \(x_1 = a\), \(x_2 = b\) et \(x = (x_1+x_2)/2\) le milieu de \([x_1,x_2]\). Si \(f(x_1).f(x) < 0\), la racine est dans \(]x_1,x[\) et on pose \(x_2 = x\); sinon la racine est dans \(]x,x_2[\) et on pose \(x_1 = x\). Puis on réitère le procédé, la longueur de l'intervalle ayant été divisée par deux. Lorsque \(x_1\) et \(x_2\) seront suffisamment proches, on décidera que la racine est \(x\).
Définir (spécification + implémentation) une fonction qui détermine le zéro d'une fonction \(f(x)\) dans \([a,b]\) selon cette méthode par dichotomie.
aide Python- Module random
Ce module permet de générer des nombres pseudo-aléatoires.
Exemple:
import random n = random.randint(0,100) e = random.choice([1,2,3,4,5,6]) p = random.random()
- Fonctions :
choice, randint, random, randrange, seed, shuffle, uniform
- Documentation officielle :
- Module math
Ce module permet de manipuler les principales fonctions mathématiques.
Exemple:
import math pi = math.pi y = math.log(math.sin(math.pi/2))
- Constantes :
pi, e
- Fonctions :
acos, acosh, asin, asinh, atan, atan2, atanh, ceil, copysign, cos, cosh, degrees, exp, fabs, factorial, floor, hypot, isnan, log, log10, pow, radians, sin, sinh, sqrt, tan, tanh, trunc
- Documentation officielle :
Votre réponse :
AAV4_DEF: Résultat
Utiliser l'interpréteur Python ci-dessous pour programmer l'algorithme demandé.
python : essai.pyOutputAAV4_DEF: Vérification
Appliquer cette technique au résultat proposé.
Si cette technique nécessite d'être implémentée en Python, le faire dans l'interpréteur Python ci-dessus (cf. Résultat), sinon développer la technique de vérification dans l'éditeur de texte ci-dessous.
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie
Une solution possible :
AAV4_DEF: Répondre explicitement à la question posée
La définition attendue est présentée dans l'interpréteur ci-dessous.
python : fonction-prop-6.pyOutputAAV4_DEF: Choisir et appliquer une technique de vérification
La vérification par jeu de tests est mise en œuvre : la fonction définie précédemment est conforme au jeu de tests.
-
