Fichier de rejeu Close
Indication Close
A propos de... Close
Commentaire Close
Téléchargements

Aide
Alternative
Ce chapitre propose de tester les acquis d'apprentissage concernant les instructions de base pour construire les algorithmes et plus particulièrement l'alternative.
Deux types de tests sont proposés :
- un test de compréhension d'une durée indicative de 30',
- un test de programmation d'une durée indicative de 60'.
Test de compréhension
-
1/5 Comprendre
-
Tests simples versus alternative simple
A l'aide d'un exemple, démontrer que l'alternative simple ci-dessous:
if condition : blocIf else : blocElse
n'est pas équivalente à la séquence de tests simples suivante:
if condition : blocIf if not condition : blocElse
Votre réponse :
AAV1_ALT: Méthode
Application de la méthode
python : essai.pyOutputAAV1_ALT: Résultat
La réponse est dans la question : ... donc l'alternative simple ci-dessous:
if condition : blocIf else : blocElse
n'est pas équivalente à la séquence de tests simples suivante:
if condition : blocIf if not condition : blocElse
Une solution possible :
AAV1_ALT: Choisir et appliquer une méthode générique
Comme précisé dans l'énoncé, on utilise la méthode du contre-exemple.
Pour prouver qu'un énoncé commençant par « Pour tout ... » (\(\forall x\)) est faux, il suffit de trouver un élément (« Il existe ... » : \(\exists y\)) qui réalise les conditions imposées dans l'hypothèse sans que ne soit vérifiée la conclusion.
On considère l'exemple suivant ou on change le signe de la variable testée (
x = -x) quelle que soit la condition :Méthode des discriminants alternative simple variables discriminantes \(x\) domaine de définition \(\mathbb{Z}\) nombres de sous-ensembles disjoints 2 définition des sous-ensembles \(]-\infty,0[\) et \([0,+\infty[\) squelette de l'alternative if x < 0 : x = -x else : x = -x
On inialise la variable discriminante de telle manière que la condition soit vraie (exemple :
x = -1).AAV1_ALT: Répondre explicitement à la question posée
Un contre-exemple est donné ci-dessous:
x = -1 print 'Deux tests simples' if x < 0 : x = -x print 'if', if not (x < 0) : x = -x print 'else', print x x1 = x x = -1 print 'Une alternative simple' if x < 0 : x = -x print 'if', else : x = -x print 'else', print x x2 = x verif = x1 == x2 print verif,x,x1,x2
-
Ordre au sein d'une alternative multiple
A l'aide d'un exemple, démontrer que l'alternative multiple ci-dessous:
if condition1 : bloc1 elif condition2 : bloc2 elif condition3 : bloc3 else : bloc4
n'est pas équivalente à l'alternative multiple suivante:
if condition1 : bloc1 elif condition3 : bloc3 elif condition2 : bloc2 else : bloc4
Votre réponse :
AAV1_ALT: Méthode
Application de la méthode
python : essai.pyOutputAAV1_ALT: Résultat
La réponse est dans la question : ... donc l'alternative multiple ci-dessous:
if condition1 : bloc1 elif condition2 : bloc2 elif condition3 : bloc3 else : bloc4
n'est pas équivalente à l'alternative multiple suivante:
if condition1 : bloc1 elif condition3 : bloc3 elif condition2 : bloc2 else : bloc4
Une solution possible :
AAV1_ALT: Choisir et appliquer une méthode générique
Comme précisé dans l'énoncé, on utilise la méthode du contre-exemple.
Pour prouver qu'un énoncé commençant par « Pour tout ... » (\(\forall x\)) est faux, il suffit de trouver un élément (« Il existe ... » : \(\exists y\)) qui réalise les conditions imposées dans l'hypothèse sans que ne soit vérifiée la conclusion.
On considère l'exemple suivant où les instructions liées à chaque sous-ensemble effectuent un traitement différent selon la valeur de
x.Méthode des discriminants permutation des elif variables discriminantes \(x\) domaine de définition \(\mathbb{Z}\) nombres de sous-ensembles disjoints 4 définition des sous-ensembles \(]-\infty,10[\) et \([10,20[\) et \([20,30[\) et \([30,+\infty[\) squelette de l'alternative if x < 10 : # sous-ensemble (x < 10) elif x < 20 : # sous-ensemble (10 <= x < 20) elif x < 30 : # sous-ensemble (20 <= x < 30) else : # sous-ensemble (30 <= x)
On initialise la variable de telle manière que la condition du premier
elifsoit vraie (exemple :x = 11).AAV1_ALT: Répondre explicitement à la question posée
Un contre-exemple est donné ci-dessous:
# exemple 1 print u'avant permutation des lignes elif' x = 11 if x < 10 : y = x/1 print 'x < 10 :',x,y elif x < 20 : y = x/2 print 'x < 20 :',x,y elif x < 30 : y = x/3 print 'x < 30 :',x,y else : y = 0 print 'x > 30 :',x,y # exemple 2 print u'après permutation des lignes elif' x = 11 if x < 10 : y = x/1 print 'x < 10 :',x,y elif x < 30 : y = x/3 print 'x < 30 :',x,y elif x < 20 : y = x/2 print 'x < 20 :',x,y else : y = 0 print 'x > 30 :',x,y
Le code précédent donne des résultats différents selon l'ordre des lignes
elif:avant permutation des lignes elif x < 20 : 11 5 après permutation des lignes elif x < 30 : 11 3
Il n'y a donc pas équivalence entre les 2 versions avant et après permutation.
-
La structure switch ... case
Certains langages, comme Javascript ou C, définissent une instruction conditionnelle
switch ... case:switch (expression) { case valeur1: // Instructions à exécuter lorsque l'évaluation // de l'expression correspond à valeur1 instructions1; [break;] case valeur2: // Instructions à exécuter lorsque l'évaluation // de l'expression correspond à valeur2 instructions2; [break;] ... case valeurN: // Instructions à exécuter lorsque l'évaluation // de l'expression à valeurN instructionsN; [break;] default: // Instructions à exécuter lorsqu'aucune des valeurs // ne correspond instructions_def; [break;] }
Une instruction
switchcommence par évaluer l'expression fournie (switch (expression)). Si une correspondance est trouvée entre la valeur de l'expression est l'un des cas proposés (valeur1,valeur2, ... ,valeurN), le programme exécute les instructions associées.Si plusieurs cas de figure correspondent, le premier cas rencontré sera sélectionné.
Le programme recherche tout d'abord une clause
casedont l'expression est évaluée avec la même valeur que l'expression d'entrée. Si une telle clause est trouvée, les instructions associées sont exécutées. Si aucune clausecasen'est trouvée, le programme recherche la clause optionnelledefaultet si elle existe, les instructions correspondantes sont exécutées. Si cette clause optionnelle n'est pas utilisée, le programme continue son exécution après l'instructionswitch.L'instruction
breakpeut optionnellement être utilisée pour chaque cas et permet de s'assurer que seules les instructions associées à ce cas seront exécutées (et le programme continue son exécution après l'instructionswitch). Sibreakn'est pas utilisé, le programme continuera son exécution avec les instructions suivantes (des autres cas de l'instructionswitch).L'exemple ci-dessous est programmé en Javascript :
javascript : alternative-def-3.jsOutputLe langage Python ne dispose pas d'une telle structure
switch. Proposer une séquence d'alternatives équivalente à la structureswitchdu programme Javascript précédent.Votre réponse :
AAV1_ALT: Méthode
Application de la méthode
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie AAV1_ALT: Résultat
Utiliser l'interpréteur Python ci-dessous pour répondre et vérifier.
python : essai.pyOutput
Une solution possible :
AAV1_ALT: Choisir et appliquer une méthode générique
On utilise la méthode des discriminants où
switch (x) ... case val:se litif x == val :etswitch (x) ... default:se litelse :.Méthode des discriminants switch ... case variables discriminantes \(x\) domaine de définition \(\mathbb{Z}\) nombres de sous-ensembles disjoints 5 définition des sous-ensembles \(]-\infty,0] \cup [5,+\infty[\) et \(\{1\}\) et \(\{2\}\) et \(\{3\}\) et \(\{4\}\) squelette de l'alternative if x == 1 : # sous-ensemble (x == 1) elif x == 2 : # sous-ensemble (x == 2) elif x == 3 : # sous-ensemble (x == 3) elif x == 4 : # sous-ensemble (x == 4) else : # sous-ensemble (x <= 0 or x >= 5)
AAV1_ALT: Répondre explicitement à la question posée
L'exemple Python ci-dessous illustre le fonctionnement équivalent au programme
switchde Javascript:# initialisation import random x = random.randint(0,9) # switch if x == 1 : text = "1" elif x == 2 : text = "234" elif x == 3 : text = "34" elif x == 4 : text = "4" else : text = "fin" # résultat print x, text
-
Alternatives en cascade (1)
Déterminer « à la main » la valeur de la variable
kaprès la séquence d'instructions suivante :1 2 3 4 5 6 7 8 9
x, y = 2, 3 d, c = 5, 4 if x > 0 and x < d : if y > 0 and y < c : k = y else : k = x else : k = 1
Votre réponse :
AAV1_ALT: Méthode
Application de la méthode
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie AAV1_ALT: Résultat
A la fin de l'algorithme, l'instruction
print kaffiche ?
Une solution possible :
AAV1_ALT: Choisir et appliquer une méthode générique
On utilise la méthode de l'empathie numérique.
On dresse la tableau des valeurs des variables instruction après instruction:
line cond x y c d k 1 - 2 3 ? ? ? 2 - 2 3 4 5 ? 3 1 2 3 4 5 ? 4 1 2 3 4 5 ? 5 - 2 3 4 5 3
AAV1_ALT: Répondre explicitement à la question posée
A la fin de l'algorithme, l'instruction
print kaffiche3:>>> print k 3
-
Alternatives en cascade (2)
Déterminer « à la main » la valeur de la variable
yaprès la séquence d'instructions suivante :1 2 3 4 5 6 7
x, y = 3, -2 if x < y : y = y - x elif x == y : y = 0 else : y = x - y
Votre réponse :
AAV1_ALT: Méthode
Application de la méthode
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie AAV1_ALT: Résultat
A la fin de l'algorithme, l'instruction
print yaffiche ?
Une solution possible :
AAV1_ALT: Choisir et appliquer une méthode générique
On utilise la méthode de l'empathie numérique.
On dresse la tableau des valeurs des variables instruction après instruction.
line cond x y 1 - 3 -2 2 0 3 -2 4 0 3 -2 6 - 3 5
AAV1_ALT: Répondre explicitement à la question posée
A la fin de l'algorithme, l'instruction
print yaffiche5:>>> print y 5
-
Test de programmation
-
1/11 Appliquer
-
Le plus grand des 3 nombres
Tirer 3 nombres entiers \(x_1\), \(x_2\), \(x_3\), aléatoirement et proposer une instruction de type « alternative » qui permettra de déterminer le plus grand des trois.
aide Pythoninstruction d'alternative (documentation Python)
if condition : bloc (elif condition : bloc)* (else : bloc)
- La notation entre parenthèses
(...)signifie que ce qui est contenu dans les parenthèses est optionnel : leelifet leelsesont donc optionnels. - L'astérisque derrière les parenthèses
(...)*signifie que l'on peut répéter 0 ou plusieurs fois le contenu des parenthèses : il peut donc y avoir autant deelifqu'on le souhaite.
- La notation entre parenthèses
nombres aléatoires (documentation Python)
import randommodule Python à importer pour manipuler des nombres aléatoires.
random.random()retourne un nombre réel aléatoirement compris entre
0inclus et1exclu.random.randint(min,max)retourne un nombre entier aléatoirement compris entre
minetmaxinclus.
Votre réponse :
AAV2_ALT: Méthode
Appliquer cette méthode au cas particulier de l'énoncé.
Texte : inputlines195.txtZone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie AAV5_ALT: Résultat
Utiliser l'interpréteur Python ci-dessous pour programmer l'algorithme demandé.
python : essai.pyOutputAAV3_ALT: Vérification
Appliquer cette technique au résultat proposé.
Si cette technique nécessite d'être implémentée en Python, le faire dans l'interpréteur ci-dessus (cf. Résultat), sinon développer la technique de vérification dans l'éditeur de texte ci-dessous.
Texte : inputlines197.txtZone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie
Une solution possible :
AAV2_ALT: Choisir et appliquer une méthode générique
On utilise la méthode des discriminants :
Méthode des discriminants le plus grand des 3 nombres variables discriminantes les 3 nombres \(x_1\), \(x_2\), \(x_3\) domaine de définition \(\mathbb{R}\) nombres de sous-ensembles disjoints 3 définition des sous-ensembles \(\{(x_1,x_2,x_3) \in \mathbb(R)| x_1 \geq x_2, x1 \geq x_3\}\) et \(\{(x_1,x_2,x_3) \in \mathbb(R)| x_2 \geq x_1, x2 \geq x_3\}\) et \(\{(x_1,x_2,x_3) \in \mathbb(R)| x_3 \geq x_1, x3 \geq x_2\}\) squelette de l'alternative if x1 >= x2 and x1 >= x3 : # sous-ensemble (x1 >= x2 and x1 >= x3) elif x2 >= x1 and x2 >= x3 : # sous-ensemble (x2 >= x1 and x2 >= x3) else : # sous-ensemble (x3 >= x1 and x3 >= x2)
AAV5_ALT: Répondre explicitement à la question posée
L'interpréteur Python ci-dessous illustre la détermination du plus grand nombre parmi 3 nombres.
python : alternative-type-number.pyOutputAAV3_ALT: Choisir et appliquer une technique de vérification
Une simple comparaison « à la main » suffit :
mest bien le plus grand des 3 nombres.
-
La plus longue des 3 chaînes
Soient 3 chaînes de caractères \(s_1\), \(s_2\) et \(s_3\). Ecrire un programme qui détermine la plus longue des 3. Si 2 chaînes ont la même longueur, on choisit celle qui est la plus grande dans l'ordre lexicographique.
aide Pythoninstruction d'alternative (documentation Python)
if condition : bloc (elif condition : bloc)* (else : bloc)
- La notation entre parenthèses
(...)signifie que ce qui est contenu dans les parenthèses est optionnel : leelifet leelsesont donc optionnels. - L'astérisque derrière les parenthèses
(...)*signifie que l'on peut répéter 0 ou plusieurs fois le contenu des parenthèses : il peut donc y avoir autant deelifqu'on le souhaite.
- La notation entre parenthèses
opérateurs de séquences (documentation Python)
x in sTruesixappartient à la séquences,Falsesinon.x not in sFalsesixappartient à la séquences,Truesinon.s + tconcaténation (mise bout à bout) de
sett.s[i]élément de rang
i+1dans la séquences(le premier élément a pour rang 0).s[i:j]séquence formée des éléments de la séquence
sdes rangsiinclus àjexclu.len(s)nombre d'éléments (longueur) de la séquence
s.s1 < s2compare les séquences
s1ets2selon l'ordre lexicographique.
Votre réponse :
AAV2_ALT: Méthode
Appliquer cette méthode au cas particulier de l'énoncé.
Texte : inputlines203.txtZone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie AAV5_ALT: Résultat
Utiliser l'interpréteur Python ci-dessous pour programmer l'algorithme demandé.
python : essai.pyOutputAAV3_ALT: Vérification
Appliquer cette technique au résultat proposé.
Si cette technique nécessite d'être implémentée en Python, le faire dans l'interpréteur ci-dessus (cf. Résultat), sinon développer la technique de vérification dans l'éditeur de texte ci-dessous.
Texte : inputlines205.txtZone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie
Une solution possible :
AAV2_ALT: Choisir et appliquer une méthode générique
On utilise la méthode des discriminants :
Méthode des discriminants La plus longue des 3 variables discriminantes \(n_1 = \mathrm{len}(s_1)\), \(n_2 = \mathrm{len}(s_2)\), \(n_3 = \mathrm{len}(s_3)\), domaine de définition \(\mathbb{N}^3\) nombres de sous-ensembles disjoints 7 définition des sous-ensembles \(\{(n_1,n_2,n_3) \in \mathbb{N}^3| n_1 > n_2, n_1 > n_3\}\) et \(\{(n_1,n_2,n_3) \in \mathbb{N}^3| n_2 > n_1, n_2 > n_3\}\) et \(\{(n_1,n_2,n_3) \in \mathbb{N}^3| n_3 > n_1, n_3 > n_2\}\) et \(\{(n_1,n_2,n_3) \in \mathbb{N}^3| n_1 = n_2, n_1 > n_3\}\) et \(\{(n_1,n_2,n_3) \in \mathbb{N}^3| n_1 = n_3, n_1 > n_2\}\) et \(\{(n_1,n_2,n_3) \in \mathbb{N}^3| n_3 = n_2, n_3 > n_1\}\) et \(\{(n_1,n_2,n_3) \in \mathbb{N}^3| n_1 = n_2 = n_3\}\) squelette de l'alternative if len(s1) > len(s2) and len(s1) > len(s3) : # elif len(s2) > len(s1) and len(s2) > len(s3) : # elif len(s3) > len(s1) and len(s3) > len(s2) : # elif len(s1) == len(s2) and len(s1) > len(s3) : # elif len(s1) == len(s3) and len(s1) > len(s2) : # elif len(s2) == len(s3) and len(s2) > len(s1) : # else : # len(s1) == len(s3) and len(s1) == len(s3)
Lorsque les longueurs des chaînes sont égales, on procède de la même manière avec l'ordre lexicographique.
AAV5_ALT: Répondre explicitement à la question posée
L'interpréteur Python ci-dessous illustre la détermination du plus grand nombre parmi 3 nombres.
python : alternative-type-string.pyOutputAAV3_ALT: Choisir et appliquer une technique de vérification
Une simple comparaison « à la main » suffit :
mest bien la plus grande des 3 chaînes.
-
Le plus grand des 3 éléments
On considère la liste \(s = [x_1,x_2,x_3]\) où \(x_1\), \(x_2\) et \(x_3\) sont 3 entiers tirés aléatoirement. Proposer une instruction de type « alternative » qui permettra de déterminer le plus grand des trois éléments.
aide Pythoninstruction d'alternative (documentation Python)
if condition : bloc (elif condition : bloc)* (else : bloc)
- La notation entre parenthèses
(...)signifie que ce qui est contenu dans les parenthèses est optionnel : leelifet leelsesont donc optionnels. - L'astérisque derrière les parenthèses
(...)*signifie que l'on peut répéter 0 ou plusieurs fois le contenu des parenthèses : il peut donc y avoir autant deelifqu'on le souhaite.
- La notation entre parenthèses
nombres aléatoires (documentation Python)
import randommodule Python à importer pour manipuler des nombres aléatoires.
random.random()retourne un nombre réel aléatoirement compris entre
0inclus et1exclu.random.randint(min,max)retourne un nombre entier aléatoirement compris entre
minetmaxinclus.opérations sur les listes (documentation Python)
x in sTruesixappartient à la séquences,Falsesinon.x not in sFalsesixappartient à la séquences,Truesinon.s + tconcaténation (mise bout à bout) de
sett.s[i]élément de rang
i+1dans la séquences(le premier élément a pour rang 0).s[i:j]séquence formée des éléments de la séquence
sdes rangsiinclus àjexclu.len(s)nombre d'éléments (longueur) de la séquence
s.s1 < s2compare les séquences
s1ets2selon l'ordre lexicographique.s.sort()trie la liste par ordre croissant de ses éléments.
Votre réponse :
AAV2_ALT: Méthode
Appliquer cette méthode au cas particulier de l'énoncé.
Texte : inputlines211.txtZone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie AAV5_ALT: Résultat
Utiliser l'interpréteur Python ci-dessous pour programmer l'algorithme demandé.
python : essai.pyOutputAAV3_ALT: Vérification
Appliquer cette technique au résultat proposé.
Si cette technique nécessite d'être implémentée en Python, le faire dans l'interpréteur ci-dessus (cf. Résultat), sinon développer la technique de vérification dans l'éditeur de texte ci-dessous.
Texte : inputlines213.txtZone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie
Une solution possible :
AAV2_ALT: Choisir et appliquer une méthode générique
On utilise la méthode des discriminants :
Méthode des discriminants le plus grand des 3 éléments variables discriminantes les 3 nombres \(x_1\), \(x_2\), \(x_3\) domaine de définition \(\mathbb{R}\) nombres de sous-ensembles disjoints 3 définition des sous-ensembles \(\{(x_1,x_2,x_3) \in \mathbb(R)| x_1 \geq x_2, x1 \geq x_3\}\) et \(\{(x_1,x_2,x_3) \in \mathbb(R)| x_2 \geq x_1, x2 \geq x_3\}\) et \(\{(x_1,x_2,x_3) \in \mathbb(R)| x_3 \geq x_1, x3 \geq x_2\}\) squelette de l'alternative if x1 >= x2 and x1 >= x3 : # sous-ensemble (x1 >= x2 and x1 >= x3) elif x2 >= x1 and x2 >= x3 : # sous-ensemble (x2 >= x1 and x2 >= x3) else : # sous-ensemble (x3 >= x1 and x3 >= x2)
AAV5_ALT: Répondre explicitement à la question posée
L'interpréteur Python ci-dessous illustre la détermination du plus grand élément d'une liste à 3 éléments.
python : alternative-type-list.pyOutputAAV3_ALT: Choisir et appliquer une technique de vérification
On utilisera la méthode prédéfinie pour trier une liste :
list.sort(): on trie la listesavec l'instructions.sort()et on compare le dernier élément de la liste triée avec le résultat précédent:>>> s.sort() >>> s[len(s)-1] == m
-
triangles sens dessus dessous
Tirer un nombre entier \(n\) aléatoirement entre 0 et 100. Puis tracer un triangle équilatéral de côté \(d = 150\) la pointe en haut si \(n\) est pair, la pointe en bas sinon.
aide Pythoninstruction d'alternative (documentation Python)
if condition : bloc (elif condition : bloc)* (else : bloc)
- La notation entre parenthèses
(...)signifie que ce qui est contenu dans les parenthèses est optionnel : leelifet leelsesont donc optionnels. - L'astérisque derrière les parenthèses
(...)*signifie que l'on peut répéter 0 ou plusieurs fois le contenu des parenthèses : il peut donc y avoir autant deelifqu'on le souhaite.
- La notation entre parenthèses
nombres aléatoires (documentation Python)
import randommodule Python à importer pour manipuler des nombres aléatoires.
random.random()retourne un nombre réel aléatoirement compris entre
0inclus et1exclu.random.randint(min,max)retourne un nombre entier aléatoirement compris entre
minetmaxinclus.tortue Logo (documentation Python)
import turtlemodule Python à importer pour manipuler la tortue Logo.
t = turtle.Turtle()crée une tortue
t.t.setheading(a)oriente la tortue
tdans une direction qui fait l'anglea(en degrés) avec l'axe horizontal (sens trigonométrique).t.forward(d)fait avancer la tortue
td'une distanceddans la direction courante.t.backward(d)fait reculer la tortue
td'une distanceddans la direction courante.t.left(a)fait tourner sur la gauche (sens trigonométrique) la tortue
t(sans avancer, ni reculer) d'un angleapar rapport à la direction courante.t.right(a)fait tourner sur la droite (sens horaire) la tortue
t(sans avancer, ni reculer) d'un angleapar rapport à la direction courante.t.goto(x,y)fait aller la tortue au point de coordonnées
(x,y)quelle que soit son orientation.
Votre réponse :
AAV2_ALT: Méthode
Appliquer cette méthode au cas particulier de l'énoncé.
Texte : inputlines219.txtZone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie AAV5_ALT: Résultat
Utiliser l'interpréteur Python ci-dessous pour programmer l'algorithme demandé.
python : essai.pyOutputAAV3_ALT: Vérification
Appliquer cette technique au résultat proposé.
Si cette technique nécessite d'être implémentée en Python, le faire dans l'interpréteur ci-dessus (cf. Résultat), sinon développer la technique de vérification dans l'éditeur de texte ci-dessous.
Texte : inputlines221.txtZone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie
Une solution possible :
AAV2_ALT: Choisir et appliquer une méthode générique
On utilise la méthode des discriminants en testant la parité avec le reste de la division par 2. Puis on applique un suivi de trajectoire pour le tracé du triangle.
Concernant le test de parité :
Méthode des discriminants triangles sens dessus dessous variables discriminantes \(n\) domaine de définition \(\mathbb{N}\) nombres de sous-ensembles disjoints 2 définition des sous-ensembles \(\{n \in \mathbb(N)| n\%2 = 0\}\) et \(\{n \in \mathbb(N)| n\%2 = 1\}\) squelette de l'alternative if n%2 == 0 : # sous-ensemble (n pair) else : # sous-ensemble (n impair)
Concernant le tracé du triangle équilatéral, on tourne à gauche si \(n\) est pair, à droite sinon :
t.forward(d) t.left(signe*120) t.forward(d) t.left(signe*120) t.forward(d)
La variable
signevaut 1 si \(n\) est pair, -1 sinon.
AAV5_ALT: Répondre explicitement à la question posée
Le code Python ci-dessous illustre le tracé du triangle selon la parité du nombre aléatoire.
python : alternative-logo-1.pyOutputAAV3_ALT: Choisir et appliquer une technique de vérification
Une simple comparaison de figures « à vue » suffit : on compare la figure obtenue avec la tortue Logo à celle attendue par l'énoncé.
On observe bien le comportement attendu.
-
Spirales rectangulaires
Tirer un nombre entier \(n\) aléatoirement entre 0 et 100. Puis tracer une spirale rectangulaire de 5 côtés de plus en plus grands si \(n\) est pair, de plus en plus petits sinon.
Le côté initial de la spirale rectangulaire est \(d = 100\), l'accroissement d'un côté à l'autre \(dx = \pm 20\).
aide Pythoninstruction d'alternative (documentation Python)
if condition : bloc (elif condition : bloc)* (else : bloc)
- La notation entre parenthèses
(...)signifie que ce qui est contenu dans les parenthèses est optionnel : leelifet leelsesont donc optionnels. - L'astérisque derrière les parenthèses
(...)*signifie que l'on peut répéter 0 ou plusieurs fois le contenu des parenthèses : il peut donc y avoir autant deelifqu'on le souhaite.
- La notation entre parenthèses
nombres aléatoires (documentation Python)
import randommodule Python à importer pour manipuler des nombres aléatoires.
random.random()retourne un nombre réel aléatoirement compris entre
0inclus et1exclu.random.randint(min,max)retourne un nombre entier aléatoirement compris entre
minetmaxinclus.tortue Logo (documentation Python)
import turtlemodule Python à importer pour manipuler la tortue Logo.
t = turtle.Turtle()crée une tortue
t.t.setheading(a)oriente la tortue
tdans une direction qui fait l'anglea(en degrés) avec l'axe horizontal (sens trigonométrique).t.forward(d)fait avancer la tortue
td'une distanceddans la direction courante.t.backward(d)fait reculer la tortue
td'une distanceddans la direction courante.t.left(a)fait tourner sur la gauche (sens trigonométrique) la tortue
t(sans avancer, ni reculer) d'un angleapar rapport à la direction courante.t.right(a)fait tourner sur la droite (sens horaire) la tortue
t(sans avancer, ni reculer) d'un angleapar rapport à la direction courante.t.goto(x,y)fait aller la tortue au point de coordonnées
(x,y)quelle que soit son orientation.
Votre réponse :
AAV2_ALT: Méthode
Appliquer cette méthode au cas particulier de l'énoncé.
Texte : inputlines227.txtZone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie AAV5_ALT: Résultat
Utiliser l'interpréteur Python ci-dessous pour programmer l'algorithme demandé.
python : essai.pyOutputAAV3_ALT:Vérification
Appliquer cette technique au résultat proposé.
Si cette technique nécessite d'être implémentée en Python, le faire dans l'interpréteur ci-dessus (cf. Résultat), sinon développer la technique de vérification dans l'éditeur de texte ci-dessous.
Texte : inputlines229.txtZone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie
Une solution possible :
AAV2_ALT: Choisir et appliquer une méthode générique
On utilise la méthode des discriminants en testant la parité avec le reste de la division par 2. Puis on applique un suivi de trajectoire pour le tracé de la spirale rectangulaire.
Concernant le test de parité :
Méthode des discriminants spirales rectangulaires variables discriminantes \(n\) domaine de définition \(\mathbb{N}\) nombres de sous-ensembles disjoints 2 définition des sous-ensembles \(\{n \in \mathbb{N}| n\%2 = 0\}\) et \(\{n \in \mathbb{N}| n\%2 = 1\}\) squelette de l'alternative if n%2 == 0 : # sous-ensemble (n pair) else : # sous-ensemble (n impair)
Concernant le tracé d'une spirale triangulaire à 5 côtés,
t.forward(d) t.left(90) t.forward(d + signe*dx) t.left(90) t.forward(d + 2*signe*dx) t.left(90) t.forward(d + 3*signe*dx) t.left(90) t.forward(d + 4*signe*dx)
La variable
signevaut 1 si \(n\) est pair, -1 sinon.
AAV5_ALT: Répondre explicitement à la question posée
L'interpréteur Python ci-dessous illustre le tracé de la spirale rectangulaire selon la parité du nombre aléatoire.
python : alternative-logo-2.pyOutputAAV3_ALT: Choisir et appliquer une technique de vérification
Une simple comparaison de figures « à vue » suffit : on compare la figure obtenue avec la tortue Logo à celle attendue par l'énoncé.
On observe bien le comportement attendu.
-
Jeu de cartes
On dispose d'un jeu de 52 cartes numérotées de 0 à 51.
Proposer deux instructions de type « alternative » qui, compte-tenu du numéro de la carte, précisent respectivement la couleur (pique, cœur, carreau, trèfle dans cet ordre) et la valeur de la carte (1, 2, ..., 10, valet, dame, roi).
- Exemples :
- 5 : 6 de pique
- 23 : valet de coeur
- 37 : dame de carreau
- 44 : 6 de trèfle
aide Pythoninstruction d'alternative (documentation Python)
if condition : bloc (elif condition : bloc)* (else : bloc)
- La notation entre parenthèses
(...)signifie que ce qui est contenu dans les parenthèses est optionnel : leelifet leelsesont donc optionnels. - L'astérisque derrière les parenthèses
(...)*signifie que l'on peut répéter 0 ou plusieurs fois le contenu des parenthèses : il peut donc y avoir autant deelifqu'on le souhaite.
Votre réponse :
AAV2_ALT: Méthode
Appliquer cette méthode au cas particulier de l'énoncé.
Texte : inputlines235.txtZone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie AAV5_ALT: Résultat
Utiliser l'interpréteur Python ci-dessous pour programmer l'algorithme demandé.
python : essai.pyOutputAAV3_ALT: Vérification
Appliquer cette technique au résultat proposé.
Si cette technique nécessite d'être implémentée en Python, le faire dans l'interpréteur ci-dessus (cf. Résultat), sinon développer la technique de vérification dans l'éditeur de texte ci-dessous.
Texte : inputlines237.txtZone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie
Une solution possible :
AAV2_ALT: Choisir et appliquer une méthode générique
Soit \(n\) le numéro de la carte (\(0 \leq n \leq 51\)): \(n\div 13\) représente la couleur (0: pique, 1: cœur, 2: carreau, 3: trèfle) et \(v = 1+n\% 13\) représente la valeur avec les correspondances évidentes (valet: 11, dame: 12, roi: 13). En d'autres termes, le quotient de la division entière \(n\div 13\) donne la couleur et le reste donne la valeur.
On détermine la couleur par une alternative multiple dont la structure est précisée par la méthode des discriminants.
Méthode des discriminants Détermination de la couleur variables discriminantes \(c = n\div 13\) domaine de définition \(E = \{0,1,2,3\}\) nombres de sous-ensembles disjoints 4 définition des sous-ensembles \(\{c \in E| c = 0\}\) et \(\{c \in E| c = 1\}\) et \(\{c \in E| c = 2\}\) et \(\{c \in E| c = 3\}\) squelette de l'alternative if c == 0 : # sous-ensemble (c == 0) elif c == 1 : # sous-ensemble (c == 1) elif c == 2 : # sous-ensemble (c == 2) else : # sous-ensemble (c == 3)
On détermine la valeur par une autre alternative multiple dont la structure est précisée par la méthode des discriminants.
Méthode des discriminants Détermination de la valeur variables discriminantes \(v = n\% 13\) domaine de définition \(E = \{0,1,2,\ldots 12\}\) nombres de sous-ensembles disjoints 4 définition des sous-ensembles \(\{v \in E| v = 10\}\) et \(\{v \in E| v = 11\}\) et \(\{v \in E| v = 12\}\) et \(\{v \in E| v < 10\}\) squelette de l'alternative if v == 10 : # sous-ensemble (v == 10) elif v == 11 : # sous-ensemble (v == 11) elif v == 12 : # sous-ensemble (v == 12) else : # sous-ensemble (0 <= v < 10)
AAV5_ALT: Répondre explicitement à la question posée
L'interpréteur Python ci-dessous donne finalement la séquence des 2 alternatives multiples pour déterminer la couleur et la valeur de la carte.
python : alternative-jeux-1.pyOutputAAV3_ALT: Choisir et appliquer une technique de vérification
On utilise la méthode du jeu de tests : l'énoncé en propose 4 et il est par ailleurs facile d'établir toutes les correspondances :
1 2 3 4 5 6 7 8 9 10 V D R pique 0 1 2 3 4 5 6 7 8 9 10 11 12 cœur 13 14 15 16 17 18 19 20 21 22 23 24 25 carreau 26 27 28 29 30 31 32 33 34 35 36 37 38 trèfle 39 40 41 42 43 44 45 46 47 48 49 50 51 Le code Python proposé vérifie bien les 4 exemples de l'énoncé ainsi que tous les autres cas possibles.
-
Catégories sportives
En 2016, les tranches d'âge pour déterminer les catégories sportives sont les suivantes (d'après le site de la Fédération française d'athlétisme) :
Catégorie Années de naissance baby 2010-2016 école d'athétisme 2007-2009 poussin 2005-2006 benjamin 2003-2004 minime 2001-2002 cadet 1999-2000 junior 1997-1998 espoir 1994-1996 sénior 1977-1993 vétéran \(\leq\) 1976 Proposer une instruction de type « alternative » qui détermine la catégorie sportive d'un athlète en fonction de son âge (exprimé en années).
Exemples:
- 6 : baby
- 10 : poussin
- 12 : benjamin
- 14 : minime
- 16 : cadet
- 18 : junior
- 20 : espoir
- 23 : sénior
- 63 : vétéran
aide Pythoninstruction d'alternative (documentation Python)
if condition : bloc (elif condition : bloc)* (else : bloc)
- La notation entre parenthèses
(...)signifie que ce qui est contenu dans les parenthèses est optionnel : leelifet leelsesont donc optionnels. - L'astérisque derrière les parenthèses
(...)*signifie que l'on peut répéter 0 ou plusieurs fois le contenu des parenthèses : il peut donc y avoir autant deelifqu'on le souhaite.
Votre réponse :
AAV2_ALT: Méthode
Appliquer cette méthode au cas particulier de l'énoncé.
Texte : inputlines243.txtZone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie AAV5_ALT: Résultat
Utiliser l'interpréteur Python ci-dessous pour programmer l'algorithme demandé.
python : essai.pyOutputAAV3_ALT: Vérification
Appliquer cette technique au résultat proposé.
Si cette technique nécessite d'être implémentée en Python, le faire dans l'interpréteur ci-dessus (cf. Résultat), sinon développer la technique de vérification dans l'éditeur de texte ci-dessous.
Texte : inputlines245.txtZone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie
Une solution possible :
AAV2_ALT: Choisir et appliquer une méthode générique
L'année de référence étant \(ref = 2016\), l'intervalle d'âges d'une catégorie est donnée par \([(ref - max),(ref-min)]\).
Une alternative multiple permettra de déterminer la catégorie en fonction de l'âge. La structure de cette alternative est précisée par la méthode des discriminants.
Méthode des discriminants Détermination de la catégorie variables discriminantes \(a = (ref-max)+1\) domaine de définition \(\mathbb{N}\) nombres de sous-ensembles disjoints 10 définition des sous-ensembles \([0,7[\) et \([7,10[\) et \([10,12[\) et \([12,14[\) et \([14,16[\) et \([16,18[\) et \([18,20[\) et \([20,23[\) et \([23,40[\) et \([40,+\infty[\) squelette de l'alternative if a < 7 : # sous-ensemble (0 <= a < 7) elif a < 10 : # sous-ensemble (7 <= a < 10) elif a < 12 : # sous-ensemble (10 <= a < 12) elif a < 14 : # sous-ensemble (12 <= a < 14) elif a < 16 : # sous-ensemble (14 <= a < 16) elif a < 18 : # sous-ensemble (16 <= a < 18) elif a < 20 : # sous-ensemble (18 <= a < 20) elif a < 23 : # sous-ensemble (20 <= a < 23) elif a < 40 : # sous-ensemble (23 <= a < 40) else : # sous-ensemble (a >= 40)
AAV5_ALT: Répondre explicitement à la question posée
L'interpréteur Python ci-dessous donne finalement l'alternative multiple pour déterminer la catégorie sportive.
python : alternative-jeux-2.pyOutputAAV3_ALT: Choisir et appliquer une technique de vérification
On utilise la méthode du jeu de tests : l'énoncé en propose 9 qui sont bien vérifiés par le code proposé.
-
Dilemme du prisonnier
Deux suspects sont arrêtés par la police. Mais les inspecteurs n'ont pas assez de preuves pour les inculper. Ils les interrogent alors séparément en leur faisant la même offre :
- Si tu dénonces ton complice et qu'il ne te dénonce pas, tu seras remis en liberté et il écopera de la peine maximale.
- Si tu le dénonces et qu'il te dénonce aussi, vous écoperez tous les deux de la moitié de la peine maximale.
- Si personne ne se dénonce, vous écoperez tous les deux de la peine minimale.
Ce dilemme se résume dans le tableau suivant où chaque case représente la peine obtenue selon le comportement des 2 suspects. Ainsi par exemple \((0;max)\) signifie que le suspect 1 sera libéré et le suspect 2 aura la peine maximale, \((max;0)\) que le suspect 1 écopera de la peine maximale et le suspect 2 sera libéré...
2 se tait 2 dénonce 1 1 se tait \((min;min)\) \((max;0)\) 1 dénonce 2 \((0;max)\) \((max/2;max/2)\) Proposer une instruction de type « alternative » qui détermine la peine encourue par chacun des 2 suspects en fonction de leur comportement.
aide Pythoninstruction d'alternative (documentation Python)
if condition : bloc (elif condition : bloc)* (else : bloc)
- La notation entre parenthèses
(...)signifie que ce qui est contenu dans les parenthèses est optionnel : leelifet leelsesont donc optionnels. - L'astérisque derrière les parenthèses
(...)*signifie que l'on peut répéter 0 ou plusieurs fois le contenu des parenthèses : il peut donc y avoir autant deelifqu'on le souhaite.
Votre réponse :
AAV2_ALT: Méthode
Appliquer cette méthode au cas particulier de l'énoncé.
Texte : inputlines251.txtZone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie AAV5_ALT: Résultat
Utiliser l'interpréteur Python ci-dessous pour programmer l'algorithme demandé.
python : essai.pyOutputAAV3_ALT: Vérification
Appliquer cette technique au résultat proposé.
Si cette technique nécessite d'être implémentée en Python, le faire dans l'interpréteur ci-dessus (cf. Résultat), sinon développer la technique de vérification dans l'éditeur de texte ci-dessous.
Texte : inputlines253.txtZone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie
Une solution possible :
AAV2_ALT: Choisir et appliquer une méthode générique
On codera « se taire » et « dénoncer l'autre » respectivement par 0 et 1. Il y a ainsi 4 cas à tester dans une alternative multiple dont la structure est précisée par la méthode des discriminants.
Méthode des discriminants Dilemme du prisonnier variables discriminantes les comportements \(n_1\) et \(n_2\) des prisonniers domaine de définition \(E = \{0,1\}^2 = \{0,1\} \times \{0,1\}\) nombres de sous-ensembles disjoints 4 définition des sous-ensembles \(\{n_1,n_2 \in \{0,1\}| n_1 = 0, n_2 = 0\}\) et \(\{n_1,n_2 \in \{0,1\}| n_1 = 0, n_2 = 1\}\) et \(\{n_1,n_2 \in \{0,1\}| n_1 = 1, n_2 = 0\}\) et \(\{n_1,n_2 \in \{0,1\}| n_1 = 1, n_2 = 1\}\) squelette de l'alternative if n1 == 0 and n2 == 0 : # évaluation de la peine elif n1 == 0 and n2 == 1 : # évaluation de la peine elif n1 == 1 and n2 == 0 : # évaluation de la peine else : # évaluation de la peine
AAV5_ALT: Répondre explicitement à la question posée
L'interpréteur Python ci-dessous donne finalement l'alternative multiple pour déterminer la peine encourue.
python : alternative-jeux-3.pyOutputAAV3_ALT: Choisir et appliquer une technique de vérification
On utilise la méthode du jeu de tests : l'énoncé décrit les 4 seuls cas possibles qui sont bien vérifiés par le code proposé.
-
Mentions au bac
Déterminer la mention au bac (ajourné, passable, assez bien, bien ou très bien) en fonction de la moyenne générale \(n\) obtenue par un bachelier.
aide Pythoninstruction d'alternative (documentation Python)
if condition : bloc (elif condition : bloc)* (else : bloc)
- La notation entre parenthèses
(...)signifie que ce qui est contenu dans les parenthèses est optionnel : leelifet leelsesont donc optionnels. - L'astérisque derrière les parenthèses
(...)*signifie que l'on peut répéter 0 ou plusieurs fois le contenu des parenthèses : il peut donc y avoir autant deelifqu'on le souhaite.
Votre réponse :
AAV2_ALT: Méthode
Appliquer cette méthode au cas particulier de l'énoncé.
Texte : inputlines259.txtZone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie AAV5_ALT: Résultat
Utiliser l'interpréteur Python ci-dessous pour programmer l'algorithme demandé.
python : essai.pyOutputAAV3_ALT: Vérification
Appliquer cette technique au résultat proposé.
Si cette technique nécessite d'être implémentée en Python, le faire dans l'interpréteur ci-dessus (cf. Résultat), sinon développer la technique de vérification dans l'éditeur de texte ci-dessous.
Texte : inputlines261.txtZone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie
Une solution possible :
AAV2_ALT: Choisir et appliquer une méthode générique
On détermine la mention au bac par une alternative multiple dont la structure est précisée par la méthode des discriminants.
Méthode des discriminants Mention au bac variables discriminantes la moyenne générale \(n\) domaine de définition \(n \in [0,20]\) nombres de sous-ensembles disjoints 5 définition des sous-ensembles \([0,10[\) et \([10,12[\) et \([12,14[\) et \([14,16[\) et \([16,20]\) squelette de l'alternative if x < 10 : # sous-ensemble (0 <= n < 10) elif x < 12 : # sous-ensemble (10 <= n < 12) elif x < 14 : # sous-ensemble (12 <= n < 14) elif x < 16 : # sous-ensemble (14 <= n < 16) else : # sous-ensemble (16 <= n <= 20)
AAV5_ALT: Répondre explicitement à la question posée
L'interpréteur Python ci-dessous donne finalement l'alternative multiple pour déterminer la mention.
python : alternative-elem-3.pyOutputAAV3_ALT: Choisir et appliquer une technique de vérification
Une simple jeu de tests suffit ici en veillant toutefois à tester toutes les branches de l'alternative.
Le programme proposé produit bien les bonnes mentions selon la note obtenue au bac.
- La notation entre parenthèses
-
Graphe de fonction
On considère la fonction \(y = f(x)\) définie sur \([-5;5]\) par le graphe ci-dessous et \(\forall x < -5, f(x) = f(-5)\) et \(\forall x > 5, f(x) = f(5)\).
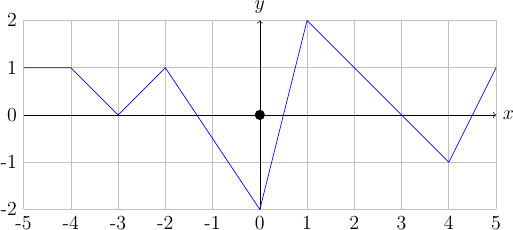
Ecrire une alternative multiple qui calcule \(y = f(x)\ \forall x \in \mathbb{R}\).
aide Pythoninstruction d'alternative (documentation Python)
if condition : bloc (elif condition : bloc)* (else : bloc)
- La notation entre parenthèses
(...)signifie que ce qui est contenu dans les parenthèses est optionnel : leelifet leelsesont donc optionnels. - L'astérisque derrière les parenthèses
(...)*signifie que l'on peut répéter 0 ou plusieurs fois le contenu des parenthèses : il peut donc y avoir autant deelifqu'on le souhaite.
Votre réponse :
AAV2_ALT: Méthode
Appliquer cette méthode au cas particulier de l'énoncé.
Texte : inputlines267.txtZone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie AAV5_ALT: Résultat
Utiliser l'interpréteur Python ci-dessous pour programmer l'algorithme demandé.
python : essai.pyOutputAAV3_ALT: Vérification
Appliquer cette technique au résultat proposé.
Si cette technique nécessite d'être implémentée en Python, le faire dans l'interpréteur ci-dessus (cf. Résultat), sinon développer la technique de vérification dans l'éditeur de texte ci-dessous.
Texte : inputlines269.txtZone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie
Une solution possible :
AAV2_ALT: Choisir et appliquer une méthode générique
La fonction \(f\) est composée d'une succession de segments de droite d'équation \(y = ax + b\) dont on peut lire directement sur le graphe la pente \(a\) et l'ordonnée à l'origine \(b\).
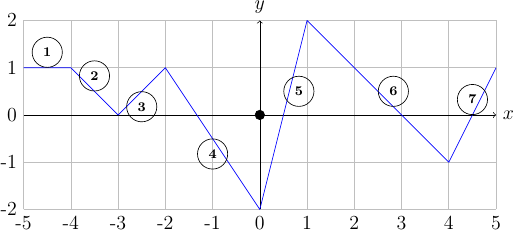
numéro équation 
\(y = 1\) 
\(y = -x -3\) 
\(y = x + 3\) 
\(y = -3x/2 - 2\) 
\(y = 4x - 2\) 
\(y = -x + 3\) 
\(y = 2x - 9\) Une alternative multiple permettra de choisir le bon segment pour calculer \(f(x)\). La méthode des discriminants permet de préciser la structure de cette alternative.
Méthode des discriminants Graphe de fonction variables discriminantes \(x\) domaine de définition \(x \in \mathbb{R}\) nombres de sous-ensembles disjoints 9 définition des sous-ensembles \(]-\infty,-5[\) et \([-5,-4[\) et \([-4,-3[\) et \([-3,-2[\) et \([-2,0[\) et \([0,1[\) et \([1,4[\) et \([4,5[\) et \([5,\infty[\) squelette de l'alternative if x < -5 : # sous-ensemble (x < -5) elif x < -4 : # sous-ensemble (-5 <= x < -4) elif x < -3 : # sous-ensemble (-4 <= x < -3) elif x < -2 : # sous-ensemble (-3 <= x < -2) elif x < 0 : # sous-ensemble (-2 <= x < 0) elif x < 1 : # sous-ensemble (0 <= x < 1) elif x < 4 : # sous-ensemble (1 <= x < 4) elif x < 5 : # sous-ensemble (4 <= x < 5) else : # sous-ensemble (5 <= x)
AAV5_ALT: Répondre explicitement à la question posée
L'interpréteur Python ci-dessous permet de calculer \(y = f(x)\).
python : alternative-prop-1.pyOutputAAV3_ALT: Choisir et appliquer une technique de vérification
On utilise la méthode du jeu de tests en comparant les valeurs obtenues par le calcul avec celles lues directement sur le graphe pour quelques points caractéristiques.
x y -10 1 -4.5 1 -3.5 0.5 -2.5 0.5 -1 -0.5 0.5 0 2 1 3 0 4.5 0 10 1 Le programme proposé conduit bien aux mêmes résultats.
- La notation entre parenthèses
-
Racines du trinôme
Ecrire un programme qui détermine la liste des racines réelles d'un trinôme \(ax^2 + bx + c\) à coefficients réels.
aide Pythoninstruction d'alternative (documentation Python)
if condition : bloc (elif condition : bloc)* (else : bloc)
- La notation entre parenthèses
(...)signifie que ce qui est contenu dans les parenthèses est optionnel : leelifet leelsesont donc optionnels. - L'astérisque derrière les parenthèses
(...)*signifie que l'on peut répéter 0 ou plusieurs fois le contenu des parenthèses : il peut donc y avoir autant deelifqu'on le souhaite.
Votre réponse :
AAV2_ALT: Méthode
Appliquer cette méthode au cas particulier de l'énoncé.
Texte : inputlines275.txtZone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie AAV5_ALT: Résultat
Utiliser l'interpréteur Python ci-dessous pour programmer l'algorithme demandé.
python : essai.pyOutputAAV3_ALT: Vérification
Appliquer cette technique au résultat proposé.
Si cette technique nécessite d'être implémentée en Python, le faire dans l'interpréteur ci-dessus (cf. Résultat), sinon développer la technique de vérification dans l'éditeur de texte ci-dessous.
Texte : inputlines277.txtZone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie
Une solution possible :
AAV2_ALT: Choisir et appliquer une méthode générique
On utilise la méthode des discriminants pour préciser la structure de l'alternative qui permet de déterminer les racines du trinôme.
- Calcul du discriminant : \(\Delta = b^2 - 4ac\)
- Etude du signe du discriminant :
- \(\Delta > 0 \Rightarrow\) 2 racines : \(\displaystyle \frac{-b \pm \sqrt{\Delta}}{2a}\)
- \(\Delta = 0 \Rightarrow\) 1 racine : \(\displaystyle \frac{-b}{2a}\)
- \(\Delta < 0 \Rightarrow\) 0 racine
Méthode des discriminants Racines du trinôme variables discriminantes le discriminant \(\Delta = b^2 - 4ac\) domaine de définition \(\mathbb{R}\) nombres de sous-ensembles disjoints 3 définition des sous-ensembles \(\Delta \in \mathbb{R}^{*-}\) et \(\Delta \in \mathbb{R}^{*+}\) et \(\Delta = 0\) squelette de l'alternative if delta < 0 : # sous-ensemble (delta < 0) elif delta == 0 : # sous-ensemble (delta == 0) else : # sous-ensemble (delta > 0)
AAV5_ALT: Répondre explicitement à la question posée
L'interpréteur Python ci-dessous permet de calculer les racines du trinôme.
python : alternative-prop-2.pyOutputAAV3_ALT: Choisir et appliquer une technique de vérification
On utilise la méthode du jeu de tests à l'aide d'identités remarquables pour chaque type de situation rencontré (ie. selon le signe du discriminant).
Discriminant Identités remarquables Racines \(\Delta < 0\) \(y = x^2 + t^2\) \(y > 0 \Rightarrow\) pas de racines \(\forall t \neq 0\) \(\Delta = 0\) \(y = (x - t)^2 = x^2 - 2xt + t^2\) \(y = 0 \Rightarrow x = t\) \(\Delta > 0\) \(y = x^2 - t^2 = (x-t)(x+t)\) \(y = 0 \Rightarrow x = \pm t\ \forall t \neq 0\) Le programme proposé retrouve bien les résultats connus pour ces identités remarquables.
- La notation entre parenthèses
-