Fichier de rejeu Close
Indication Close
A propos de... Close
Commentaire Close
Téléchargements
Aide
Affectation
Ce chapitre propose de tester les acquis d'apprentissage concernant les instructions de base pour construire les algorithmes et plus particulièrement l'affectation.
Deux types de tests sont proposés :
- un test de compréhension d'une durée indicative de 30',
- un test de programmation d'une durée indicative de 60'.
Test de compréhension
-
1/7 Comprendre
-
Division entière
Déterminer « à la main » les valeurs des variables
a,b,qetraprès la séquence d'affectations suivante :a = 23 b = 5 q = 0 r = a r = r - b q = q + 1 r = r - b q = q + 1 r = r - b q = q + 1 r = r - b q = q + 1
opérateurs arithmétiquesa+bsomme : \(a+b\)
a-bdifférence : \(a-b\)
a*bproduit : \(a*b\)
a/bdivision : \(a/b\)
Remarque : division entière si
aetbsont entiers, le résultat est alors le quotient de la division entière.a%breste de la division entière : \(a\%b = a \mod b\)
x**nélévation à la puissance : \(x^n\).
Votre réponse :
AAV1_AFF: Méthode
Application de la méthode
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie AAV1_AFF: Résultat
A la fin de l'algorithme, l'instruction
print a, b, q, raffiche ?
Une solution possible :
- AAV1_AFF: Méthode
On dresse, instruction après instruction, le tableau d'évolution des valeurs de toutes les variables qui interviennent dans l'algorithme.
inst a b q r 1 23 ? ? ? 2 23 5 ? ? 3 23 5 0 ? 4 23 5 0 23 5 23 5 0 18 6 23 5 1 18 7 23 5 1 13 8 23 5 2 13 9 23 5 2 8 10 23 5 3 8 11 23 5 3 3 12 23 5 4 3
- AAV1_AFF: Résultat
A la fin de l'algorithme, les valeurs des variables a, b, q et r sont respectivement 23, 5, 4 et 3.
>>> print a, b, q, r 23 5 4 3
Remarque : a = b * q + r
-
Plus grand commun diviseur
Déterminer « à la main » les valeurs des variables
a,betraprès la séquence d'affectations suivante:a = 63 b = 270 r = a % b # reste de la division de a par b a = b b = r r = a % b a = b b = r r = a % b a = b b = r r = a % b a = b b = r
opérateurs arithmétiquesa+bsomme : \(a+b\)
a-bdifférence : \(a-b\)
a*bproduit : \(a*b\)
a/bdivision : \(a/b\)
Remarque : division entière si
aetbsont entiers, le résultat est alors le quotient de la division entière.a%breste de la division entière : \(a\%b = a \mod b\)
x**nélévation à la puissance : \(x^n\).
Votre réponse :
AAV1_AFF: Méthode
Application de la méthode
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie AAV1_AFF: Résultat
A la fin de l'algorithme, l'instruction
print a, b ,raffiche ?
Une solution possible :
- AAV1_AFF: Méthode
On dresse, instruction après instruction, le tableau d'évolution des valeurs de toutes les variables qui interviennent dans l'algorithme.
inst a b r 1 63 ? ? 2 63 270 ? 3 63 270 63 4 270 270 63 5 270 63 63 6 270 63 18 7 63 63 18 8 63 18 18 9 63 18 9 10 18 18 9 11 18 9 9 12 18 9 0 13 9 9 0 14 9 0 0
- AAV1_AFF: Résultat
A la fin de l'algorithme, les valeurs des variables a, b et r sont respectivement 9, 0 et 0.
>>> print a, b, r 9 0 0
Remarque : 9 = pgcd(63, 270)
-
Nombres de Fibonacci
Déterminer « à la main » les valeurs des variables
n,f1,f2etfaprès la séquence d'affectations suivante:n = 3 f1 = 2 f2 = 1 f = f1 + f2 n = n + 1 f2 = f1 f1 = f f = f1 + f2 n = n + 1 f2 = f1 f1 = f f = f1 + f2 n = n + 1 f2 = f1 f1 = f f = f1 + f2
opérateurs arithmétiquesa+bsomme : \(a+b\)
a-bdifférence : \(a-b\)
a*bproduit : \(a*b\)
a/bdivision : \(a/b\)
Remarque : division entière si
aetbsont entiers, le résultat est alors le quotient de la division entière.a%breste de la division entière : \(a\%b = a \mod b\)
x**nélévation à la puissance : \(x^n\).
Votre réponse :
AAV1_AFF: Méthode
Application de la méthode
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie AAV1_AFF: Résultat
A la fin de l'algorithme, l'instruction
print n, f1, f2, faffiche ?
Une solution possible :
- AAV1_AFF: Méthode
On dresse, instruction après instruction, le tableau d'évolution des valeurs de toutes les variables qui interviennent dans l'algorithme.
inst n f1 f2 f 1 3 ? ? ? 2 3 2 ? ? 3 3 2 1 ? 4 3 2 1 3 5 4 2 1 3 6 4 2 2 3 7 4 3 2 3 8 4 3 2 5 9 5 3 2 5 10 5 3 3 5 11 5 5 3 5 12 5 5 3 8 13 6 5 3 8 14 6 5 5 8 15 6 8 5 8 16 6 8 5 13
- AAV1_AFF: Résultat
A la fin de l'algorithme, les valeurs des variables n, f1, f2 et f sont respectivement
>>> print n, f1, f2 ,f 6 8 5 13
- Remarque :
La valeur finale de f (13) est le nombre de Fibonacci à l'ordre n (6) :
\(\displaystyle\left|\begin{array}{llll} f_0 &=& 1 & \\ f_1 &=& 1 & \\ f_n &=& f_{n-1} + f_{n-2} & \forall n \in \mathbb{N}, n > 1 \end{array}\right.\Rightarrow\left|\begin{array}{llll} f_2 &=& 1+1 &=& 2\\ f_3 &=& 2+1 &=& 3\\ f_4 &=& 3+2 &=& 5\\ f_5 &=& 5+3 &=& 8\\ f_6 &=& 8+5 &=& 13\\ f_7 &=& 13+8 &=& 21\\ f_8 &=& 21+13 &=& 34\\ f_9 &=& 34+21 &=& 55\\ f_{10} &=& 55+34 &=& 89\\ \ldots \end{array}\right.\)
-
Elévation à la puissance
Déterminer « à la main » les valeurs des variables
x,netpaprès la séquence d'affectations suivante :x = 3 n = 0 p = 1 n = n + 1 p = p * x n = n + 1 p = p * x n = n + 1 p = p * x n = n + 1 p = p * x
opérateurs arithmétiquesa+bsomme : \(a+b\)
a-bdifférence : \(a-b\)
a*bproduit : \(a*b\)
a/bdivision : \(a/b\)
Remarque : division entière si
aetbsont entiers, le résultat est alors le quotient de la division entière.a%breste de la division entière : \(a\%b = a \mod b\)
x**nélévation à la puissance : \(x^n\).
Votre réponse :
AAV1_AFF: Méthode
Application de la méthode
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie AAV1_AFF: Résultat
A la fin de l'algorithme, l'instruction
print x, n, paffiche ?
Une solution possible :
- AAV1_AFF: Méthode
On dresse, instruction après instruction, le tableau d'évolution des valeurs de toutes les variables qui interviennent dans l'algorithme.
inst x n p 1 3 ? ? 2 3 0 ? 3 3 0 1 4 3 1 1 5 3 1 3 6 3 2 3 7 3 2 9 8 3 3 9 9 3 3 27 10 3 4 27 11 3 4 81
- AAV1_AFF: Résultat
A la fin de l'algorithme, les valeurs des variables x, n et p sont respectivement
>>> print x, n, p 3 4 81
- Remarque :
La valeur finale de p (81) correspond à la valeur de x (3) élevée à la puissance n (4) : \(p = x ^ n\ (81 = 3 ^ 4)\).
-
Décalage à gauche
Remettre les 5 instructions ci-dessous dans le bon ordre pour obtenir un algorithme qui opère un décalage à gauche des valeurs des 3 variables
u,v,w.Exemple de décalage à gauche:
- Avant décalage :
u, v, w = 1, 2, 3- Après décalage à gauche :
u, v, w = 2, 3, 1
Votre réponse :
AAV1_AFF: Résultat
AAV1_AFF: Résultat
1. Ordonner les instructions
u, v, w = 1, 2, 3tmp = uu = vv = ww = tmp
/0/: Commencer par initialiser les variables. /1/: Sauvegarder une des valeurs initiales dans une variable temporaire. En utilisant les n-uplets de Python, on aurait pu écrire plus directement:
u, v, w = 1, 2, 3 u, v, w = v, w, u
AAV1_AFF: Vérification
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie
Une solution possible :
AAV1_AFF: Répondre explicitement à la question posée
L'ordre recherché est donc le suivant:
u, v, w = 1, 2, 3 tmp = u u = v v = w w = tmp
AAV1_AFF: Choisir et appliquer une technique de vérification
On utilise la méthode de l'empathie numérique pour vérifier « à la main » le résultat proposé:
inst u v w tmp 1 1 2 3 ? 2 1 2 3 1 3 2 2 3 1 4 2 3 3 1 5 2 3 1 1
-
Décalage à droite
Remettre les 7 instructions ci-dessous dans le bon ordre pour obtenir un algorithme qui opère un décalage à droite des valeurs des 5 variables
u,v,x,y,z.Exemple décalage à droite:
- Avant décalage :
u, v, x, y, z = 1, 2, 3, 4, 5- Après décalage à droite :
u, v, x, y, z = 5, 1, 2, 3, 4
Votre réponse :
AAV1_AFF: Résultat
AAV1_AFF: Résultat
1. Ordonner les instructions
u, v, x, y, z = 1, 2, 3, 4, 5tmp = zz = yy = xx = vv = uu = tmp
/0/: On commence par initialiser les variables. /1/: On sauvegarde une des valeurs initiales dans une variable temporaire. En utilisant les n-uplets de Python, on aurait pu écrire plus directement:
u, v, x, y, z = 1, 2, 3, 4, 5 u, v, x, y, z = z, u, v, x, y
AAV1_AFF: Vérification
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie
Une solution possible :
AAV1_AFF: Répondre explicitement à la question posée
L'ordre recherché est donc le suivant:
u, v, x, y, z = 1, 2, 3, 4, 5 tmp = z z = y y = x x = v v = u u = tmp
AAV1_AFF: Choisir et appliquer une technique de vérification
On utilise la méthode de l'empathie numérique pour vérifier « à la main » le résultat proposé:
inst u v x y z tmp 1 1 2 3 4 5 ? 2 1 2 3 4 5 5 3 1 2 3 4 4 5 4 1 2 3 3 4 5 5 1 2 2 3 4 5 6 1 1 2 3 4 5 7 5 1 2 3 4 5
-
Décalages alternés
Remettre les 9 instructions ci-dessous dans le bon ordre pour obtenir un algorithme qui opère d'abord un décalage à gauche des valeurs des 3 variables de rang impair
u,wetypuis un décalage à droite des valeurs des 3 variables de rang pairv,xetz.Exemple de décalage alterné :
- Avant décalage :
u, v, w, x, y, z = 1, 2, 3, 4, 5, 6- Après le décalage alterné proposé :
u, v, w, x, y, z = 3, 6, 5, 2, 1, 4
Votre réponse :
AAV1_AFF: Résultat
AAV1_AFF: Résultat
1. Décalages
u, v, w, x, y, z = 1, 2, 3, 4, 5, 6t1 = ut2 = zu = ww = yy = t1z = xx = vv = t2
/0/: On commence par initialiser les variables. /1/: On sauvegarde une des valeurs initiales dans une variable temporaire. /5/: On sauvegarde une des valeurs initiales dans une variable temporaire. En utilisant les n-uplets de Python, on aurait pu écrire plus directement:
u, v, w, x, y, z = 1, 2, 3, 4, 5, 6 u, v, w, x, y, z = w, z, y, v, u, x
AAV1_AFF: Vérification
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie
Une solution possible :
AAV1_AFF: Répondre explicitement à la question posée
L'ordre recherché est donc le suivant:
u, v, w, x, y, z = 1, 2, 3, 4, 5, 6 t1 = u t2 = z u = w w = y y = t1 z = x x = v v = t2
AAV1_AFF: Choisir et appliquer une technique de vérification
On utilise la méthode de l'empathie numérique pour vérifier « à la main » le résultat proposé:
inst u v w x y z t1 t2 1 1 2 3 4 5 6 ? ? 2 1 2 3 4 5 6 1 ? 3 1 2 3 4 5 6 1 6 4 3 2 3 4 5 6 1 6 5 3 2 5 4 5 6 1 6 6 3 2 5 4 1 6 1 6 7 3 2 5 4 1 4 1 6 8 3 2 5 2 1 4 1 6 9 3 6 5 2 1 4 1 6
-
Test de programmation
-
1/14 Appliquer
-
Circuit logique
On considère le circuit logique ci-dessous où \(a\) et \(b\) sont les entrées et \(s\) la sortie.
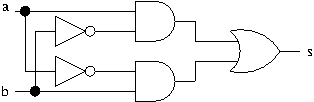
Proposer une instruction de type « affectation » qui permettra de calculer la sortie \(s\) du circuit lorsque les entrées \(a\) et \(b\) sont toutes à \(1\).
opérateurs booléens
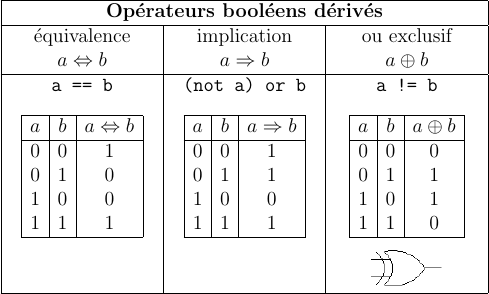aide Pythoninstruction d'affectation
a = baffecte la valeur de l'expression
bà la variable de noma.opérateurs booléens (documentation Python)
not anégation : \(\overline{a}\)
a and bconjonction : \(a\cdot b\)
a or bdisjonction : \(a + b\)
Votre réponse :
AAV2_AFF: Méthode
Application de la méthode
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie AAV5_AFF: Résultat
Utiliser l'interpréteur Python ci-dessous pour répondre.
python : essai.pyOutputAAV3_AFF: Vérification
Application de la technique
Si la technique proposée nécessite Python, on la mettra en œuvre dans l'interpréteur ci-dessus (cf. Résultat).
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie
Une solution possible :
AAV2_AFF: Choisir et appliquer une méthode générique
On utilise une représentation analytique. En effet, lorsque un objet est représenté sous une forme graphique, il est préférable de le transformer en sa représentation analytique (lorsqu'elle existe) pour étudier cet objet à l'aide d'un programme informatique.
Le circuit logique de l'énoncé possède 2 entrées
aetbet une sorties; sa représentation analytique est simplement:s = (not a and b) or (a and not b)
Il faut bien sûr initialiser
aetbpour que l'expression du membre de droite soit évaluable.AAV5_AFF: Répondre explicitement à la question posée
L'instruction de type affectation qui permet de simuler le circuit logique est donnée dans l'interpréteur ci-dessous.
python : affectation-type-boolean.pyOutputAAV3_AFF: Choisir et appliquer une technique de vérification
On établit « à la main » la table de vérité du circuit et on compare le résultat obtenu par programme avec celui de la table établie à la main.
\(a\) \(b\) \(s\) 0 0 0 0 1 1 1 0 1 1 1 0 On constate que ce circuit réalise un « ou exclusif » (xor, \(\oplus\)). Lorsque les entrées \(a\) et \(b\) sont à 1 (dernière ligne de la table de vérité), la sortie \(s\) est à 0 (
False).Le code Python précédent donne bien le même résultat.
On peut également utiliser le simulateur de circuits logiques ci-dessous pour vérifier le résultat fourni par le code Python.
Circuit logique : affectation-circuit.jsonEntrées/Sorties
Portes 1/1
Portes 2/1
Portes 3/1
Vue d'ensemble
-
Appartenance à une liste
Proposer une instruction de type « affectation » qui permettra de tester si les entiers
3ou9appartiennent à la liste['salut',1.72,4,True,6,'3'].aide Pythoninstruction d'affectation
a = baffecte la valeur de l'expression
bà la variable de noma.opérateurs de séquences (documentation Python)
x in sTruesixappartient à la séquences,Falsesinon.x not in sFalsesixappartient à la séquences,Truesinon.s + tconcaténation (mise bout à bout) de
sett.s[i]élément de rang
i+1dans la séquences(le premier élément a pour rang 0).s[i:j]séquence formée des éléments de la séquence
sdes rangsiinclus àjexclu.len(s)nombre d'éléments (longueur) de la séquence
s.
Votre réponse :
AAV2_AFF: Méthode
Application de la méthode
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie AAV5_AFF: Résultat
Utiliser l'interpréteur Python ci-dessous pour répondre.
python : essai.pyOutputAAV3_AFF: Vérification
Application de la technique
Si la technique proposée nécessite Python, on la mettra en œuvre dans l'interpréteur ci-dessus (cf. Résultat).
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie
Une solution possible :
AAV2_AFF: Choisir et appliquer une méthode générique
On commence par faire abstraction des données spécifiques, en particulier numériques ou alphanumériques, pour ne considérer que les variables associées. Puis on reformule l'énoncé avec les noms des variables en explicitant les données du problème et les résultats attendus.
Ainsi, on ne s'intéressera pas aux valeurs
3,9ou['salut',1.72,4,True,6,'3']mais plutôt à ce qu'elles qualifient : deux entiers et une liste auxquels on attribuera un nom chacun.Il s'agit donc ici de tester si une liste
tcontient l'un ou l'autre des 2 élémentse1ete2. On utilise pour cela l'opérateurin:present = (e1 in t) or (e2 in t)
AAV5_AFF: Répondre explicitement à la question posée
L'instruction de type affectation qui permet de répondre à la question posée est donnée dans l'interpréteur ci-dessous.
python : affectation-type-list.pyOutputAAV3_AFF: Choisir et appliquer une technique de vérification
On vérifie simplement par une simple comparaison avec un calcul « à la main ». En effet, la liste est suffisamment petite pour vérifier « à la main » la présence ou non de l'un ou l'autre des éléments.
L'élément
'3'n'est pas un entier, mais une chaîne de caractères. La listetne contient donc ni l'entier 3, ni l'entier 9, d'où le résultatFalseobtenu après exécution du code.
-
Longueur d'une chaîne
Proposer une instruction de type « affectation » qui permettra de tester si les deux chaînes de caractères
'bonjour'et'salut'ont le même nombre d'éléments.aide Pythoninstruction d'affectation
a = baffecte la valeur de l'expression
bà la variable de noma.opérateurs de séquences (documentation Python)
x in sTruesixappartient à la séquences,Falsesinon.x not in sFalsesixappartient à la séquences,Truesinon.s + tconcaténation (mise bout à bout) de
sett.n*sconcaténation de
savec elle-même,nfois.s[i]élément de rang
i+1dans la séquences(le premier élément a pour rang 0).s[i:j]séquence formée des éléments de la séquence
sdes rangsiinclus àjexclu.len(s)nombre d'éléments (longueur) de la séquence
s.
Votre réponse :
AAV2_AFF: Méthode
Application de la méthode
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie AAV5_AFF: Résultat
Utiliser l'interpréteur Python ci-dessous pour répondre.
python : essai.pyOutputAAV3_AFF: Vérification
Application de la technique
Si la technique proposée nécessite Python, on la mettra en œuvre dans l'interpréteur ci-dessus (cf. Résultat).
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie
Une solution possible :
AAV2_AFF: Choisir et appliquer une méthode générique
On commence par faire abstraction des données spécifiques, en particulier numériques ou alphanumériques, pour ne considérer que les variables associées. Puis on reformule l'énoncé avec les noms des variables en explicitant les données du problème et les résultats attendus.
Ainsi, on ne s'intéressera pas aux valeurs alphanumériques
'bonjour'et'salut'mais plutôt à ce qu'elles qualifient : deux chaînes de caractères auxquelles on attribuera un nom chacune.Il s'agit donc ici de comparer les longueurs de deux chaînes
s1ets2. La longueur d'une chaîne de caractères s'obtient à l'aide de la fonctionlen:len(s1)oulen(s2). On affecte donc simplement la comparaison(len(s1) == len(s2))à la réponse souhaitée:compar = (len(s1) == len(s2))
comparprendra donc la valeur booléenneTrueouFalseselon que les longueurs sont égales ou non.AAV5_AFF: Répondre explicitement à la question posée
L'instruction de type affectation qui permet de répondre à la question posée est donnée dans l'interpréteur ci-dessous.
python : affectation-type-string.pyOutputAAV3_AFF: Choisir et appliquer une technique de vérification
On vérifie simplement par une comparaison avec un calcul « à la main ». En effet, les chaînes de caractères sont suffisamment petites pour calculer « à la main » leur nombre de caractères et les comparer.
La chaîne
bonjoura 7 caractères, la chaînesaluten a 5 : elles ne sont donc pas de longueurs égales, d'où le résultatFalseobtenu après exécution du code.
-
Triangle rectangle
On considère le triangle \(ABC\) rectangle en \(A\) de la figure ci-dessous. Le côté \((AB)\) de longueur \(c = 200\) fait un angle \(\theta = 30^\circ\) avec l'axe des \(x\). Le côté \((AC)\) a pour longueur \(b = 150\).
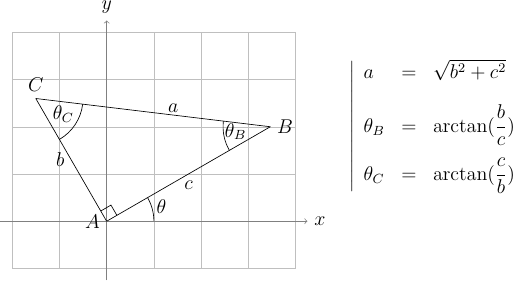
Proposer un algorithme pour faire dessiner ce triangle rectangle par la tortue Logo en utilisant uniquement des instructions de type « affectation » et des instructions de la tortue Logo.
aide Pythoninstruction d'affectation
a = baffecte la valeur de l'expression
bà la variable de noma.tortue Logo : (documentation Python)
import turtlemodule Python à importer pour manipuler la tortue Logo.
t = turtle.Turtle()crée une tortue
t.t.down()tracer la trajectoire de la tortue Logo.
t.up()ne pas tracer la trajectoire de la tortue Logo.
t.setheading(a)oriente la tortue
tdans une direction qui fait l'anglea(en degrés) avec l'axe horizontal (sens trigonométrique).t.forward(d)fait avancer la tortue
td'une distanceddans la direction courante.t.backward(d)fait reculer la tortue
td'une distanceddans la direction courante.t.left(a)fait tourner sur la gauche (sens trigonométrique) la tortue
t(sans avancer, ni reculer) d'un angleapar rapport à la direction courante.t.right(a)fait tourner sur la droite (sens horaire) la tortue
t(sans avancer, ni reculer) d'un angleapar rapport à la direction courante.t.goto(x,y)fait aller la tortue au point de coordonnées
(x,y)quelle que soit son orientation.
Votre réponse :
AAV2_AFF: Méthode
Application de la méthode
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie AAV5_AFF: Résultat
Utiliser l'interpréteur Python ci-dessous pour répondre.
python : essai.pyOutputAAV3_AFF: Vérification
Application de la technique
Si la technique proposée nécessite Python, on la mettra en œuvre dans l'interpréteur ci-dessus (cf. Résultat).
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie
Une solution possible :
AAV2_AFF: Choisir et appliquer une méthode générique
On effectuera un suivi de trajectoire : voir la figure à dessiner comme une trajectoire à faire parcourir par la tortue Logo.
La trigonométrie du triangle rectangle \(ABC\) permet de déterminer les éléments manquants pour le suivi de trajectoire : le troisième côté \(a\) et les deux autres angles \(\theta_B\) et \(\theta_C\) respectivement en \(B\) et en \(C\).
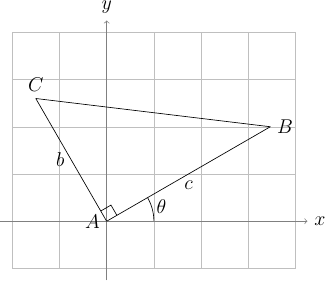
Une fois connus les 3 côtés \(a\), \(b\), \(c\) et les 3 angles du triangle \(\theta_A\), \(\theta_B\), \(\theta_C\), il reste à déplacer la tortue en « suivant » le triangle côté après côté.
On commence par créer la tortue
t:t = turtle.Turtle().Le suivi de trajectoire commence par orienter correctement la tortue
t:t.setheading(theta).On fait avancer la tortue de la longueur du côté \((AB)\) :
t.forward(c).On la fait tourner sur la gauche :
t.left(180-thetaB)puis on décrit le côté \((BC)\) :t.forward(a), et ainsi de suite jusqu'à revenir au point de départ \(A\).RemarqueCe suivi de trajectoire ne dépend pas du type du triangle (rectangle, isocèle, équilatéral, quelconque...).
AAV5_AFF: Répondre explicitement à la question posée
Les instructions qui permettent de répondre à la question posée est donnée dans l'interpréteur ci-dessous.
python : affectation-logo-1.pyOutputAAV3_AFF: Choisir et appliquer une technique de vérification
Une simple comparaison des figures suffit : on compare la figure obtenue avec la tortue Logo à celle de l'énoncé.
Le triangle obtenu correspond bien à celui de l'énoncé.
-
Triangle équilatéral
On considère le triangle équilatéral \(ABC\) de la figure ci-dessous. Il a pour côté \(a = 130\) et le côté \((AB)\) fait un angle de \(\theta = 50^\circ\) avec l'axe des \(x\).
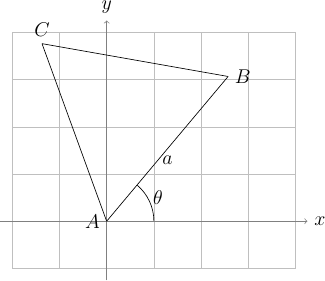
Proposer un algorithme pour faire dessiner ce triangle équilatéral par la tortue Logo en utilisant uniquement des instructions de type « affectation » et des instructions de la tortue Logo.
aide Pythoninstruction d'affectation
a = baffecte la valeur de l'expression
bà la variable de noma.tortue Logo : (documentation Python)
import turtlemodule Python à importer pour manipuler la tortue Logo.
t = turtle.Turtle()crée une tortue
t.t.down()tracer la trajectoire de la tortue Logo.
t.up()ne pas tracer la trajectoire de la tortue Logo.
t.setheading(a)oriente la tortue
tdans une direction qui fait l'anglea(en degrés) avec l'axe horizontal (sens trigonométrique).t.forward(d)fait avancer la tortue
td'une distanceddans la direction courante.t.backward(d)fait reculer la tortue
td'une distanceddans la direction courante.t.left(a)fait tourner sur la gauche (sens trigonométrique) la tortue
t(sans avancer, ni reculer) d'un angleapar rapport à la direction courante.t.right(a)fait tourner sur la droite (sens horaire) la tortue
t(sans avancer, ni reculer) d'un angleapar rapport à la direction courante.t.goto(x,y)fait aller la tortue au point de coordonnées
(x,y)quelle que soit son orientation.
Votre réponse :
AAV2_AFF: Méthode
Application de la méthode
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie AAV5_AFF: Résultat
Utiliser l'interpréteur Python ci-dessous pour répondre.
python : essai.pyOutputAAV3_AFF: Vérification
Application de la technique
Si la technique proposée nécessite Python, on la mettra en œuvre dans l'interpréteur ci-dessus (cf. Résultat).
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie
Une solution possible :
AAV2_AFF: Choisir et appliquer une méthode générique
On effectuera un suivi de trajectoire : voir la figure à dessiner comme une trajectoire à faire parcourir par la tortue Logo.
On commence par s'abstraire des données spécifiques à la question en introduisant des noms de variable et en appliquant les résultats élémentaires de trigonométrie du triangle équilatéral : dans un triangle équilatéral, les 3 côtés sont égaux et les 3 angles aussi:
# données de l'énoncé a = b = c = 130. thetaA = thetaB = thetaC = 60. theta = 50.
On pourra ainsi dessiner n'importe quel triangle équilatéral dont on connaîtra
aettheta.Une fois connus les 3 côtés et les 3 angles du triangle, il reste à déplacer la tortue en « suivant » le triangle côté après côté.
On commence par créer la tortue
t:t = turtle.Turtle().Le suivi de trajectoire commence par orienter correctement la tortue
t:t.setheading(theta).On fait avancer la tortue de la longueur du côté \((AB)\) :
t.forward(c).On la fait tourner sur la gauche :
t.left(180-thetaB)puis on décrit le côté \((BC)\) :t.forward(a), et ainsi de suite jusqu'à revenir au point de départ \(A\).RemarqueCe suivi de trajectoire ne dépend pas du type du triangle (rectangle, isocèle, équilatéral, quelconque...).
AAV5_AFF: Répondre explicitement à la question posée
Les instructions qui permettent de répondre à la question posée est donnée dans l'interpréteur ci-dessous.
python : affectation-logo-2.pyOutputAAV3_AFF: Choisir et appliquer une technique de vérification
Une simple comparaison des figures suffit : on compare la figure obtenue avec la tortue Logo à celle de l'énoncé.
Le triangle obtenu correspond bien à celui de l'énoncé.
-
Triangle quelconque
On considère le triangle \(ABC\) de la figure ci-dessous. Il a pour côté \(a = 30\sqrt{5}\), \(b = 30\sqrt{13}\) et \(c = 120\). Les angles en \(A\) et en \(B\) valent respectivement \(\arctan(2/3.)\) et \(\arctan(2.)\). Le côté \((AB)\) fait un angle \(\theta = 20^\circ\) avec l'axe des \(x\).
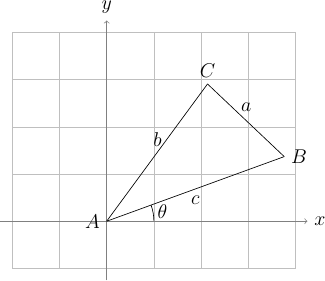
Proposer un algorithme pour faire dessiner ce triangle équilatéral par la tortue Logo en utilisant uniquement des instructions de type « affectation » et des instructions de la tortue Logo.
aide Pythoninstruction d'affectation
a = baffecte la valeur de l'expression
bà la variable de noma.tortue Logo : (documentation Python)
import turtlemodule Python à importer pour manipuler la tortue Logo.
t = turtle.Turtle()crée une tortue
t.t.down()tracer la trajectoire de la tortue Logo.
t.up()ne pas tracer la trajectoire de la tortue Logo.
t.setheading(a)oriente la tortue
tdans une direction qui fait l'anglea(en degrés) avec l'axe horizontal (sens trigonométrique).t.forward(d)fait avancer la tortue
td'une distanceddans la direction courante.t.backward(d)fait reculer la tortue
td'une distanceddans la direction courante.t.left(a)fait tourner sur la gauche (sens trigonométrique) la tortue
t(sans avancer, ni reculer) d'un angleapar rapport à la direction courante.t.right(a)fait tourner sur la droite (sens horaire) la tortue
t(sans avancer, ni reculer) d'un angleapar rapport à la direction courante.t.goto(x,y)fait aller la tortue au point de coordonnées
(x,y)quelle que soit son orientation.
Votre réponse :
AAV2_AFF: Méthode
Application de la méthode
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie AAV5_AFF: Résultat
Utiliser l'interpréteur Python ci-dessous pour répondre.
python : essai.pyOutputAAV3_AFF: Vérification
Application de la technique
Si la technique proposée nécessite Python, on la mettra en œuvre dans l'interpréteur ci-dessus (cf. Résultat).
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie
Une solution possible :
AAV2_AFF: Choisir et appliquer une méthode générique
On effectuera un suivi de trajectoire : voir la figure à dessiner comme une trajectoire à faire parcourir par la tortue Logo.
On commence par s'abstraire des données spécifiques à la question en introduisant des noms de variable et en appliquant les résultats élémentaires de trigonométrie du triangle quelconque:
# données de l'énoncé a, b, c = 30.*sqrt(5.), 30.*sqrt(13.), 120. thetaA, thetaB = atan(2/3.)*180/pi, atan(2.)*180/pi theta = 20. # géométrie du triangle quelconque thetaC = 180. - (thetaA + thetaB)
On pourra ainsi dessiner n'importe quel triangle quelconque dont on connaîtra
aettheta.Une fois connus les 3 côtés et les 3 angles du triangle, il reste à déplacer la tortue en « suivant » le triangle côté après côté.
On commence par créer la tortue
t:t = turtle.Turtle().Le suivi de trajectoire commence par orienter correctement la tortue
t:t.setheading(theta).On fait avancer la tortue de la longueur du côté \((AB)\) :
t.forward(c).On la fait tourner sur la gauche :
t.left(180-thetaB)puis on décrit le côté \((BC)\) :t.forward(a), et ainsi de suite jusqu'à revenir au point de départ \(A\).RemarqueCe suivi de trajectoire ne dépend pas du type du triangle (rectangle, isocèle, équilatéral, quelconque...).
AAV5_AFF: Répondre explicitement à la question posée
Les instructions qui permettent de répondre à la question posée est donnée dans l'interpréteur ci-dessous.
python : affectation-logo-3.pyOutputAAV3_AFF: Choisir et appliquer une technique de vérification
Une simple comparaison de figures suffit : on compare la figure obtenue avec la tortue Logo à celle de l'énoncé.
Le triangle obtenu correspond bien à celui de l'énoncé.
-
Lancer de dés
Proposer une instruction de type « affectation » qui permettra de simuler un lancer de dé à 6 faces.
aide Pythoninstruction d'affectation
a = baffecte la valeur de l'expression
bà la variable de noma.nombres aléatoires (documentation Python)
import randommodule Python à importer pour manipuler des nombres aléatoires.
random.random()retourne un nombre réel aléatoirement compris entre
0inclus et1exclu.random.randint(min,max)retourne un nombre entier aléatoirement compris entre
minetmaxinclus.
Votre réponse :
AAV2_AFF: Méthode
Application de la méthode
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie AAV5_AFF: Résultat
Utiliser l'interpréteur Python ci-dessous pour programmer l'algorithme demandé.
python : essai.pyOutputAAV3_AFF: Vérification
Application de la technique
Si la technique proposée nécessite Python, on la mettra en œuvre dans l'interpréteur ci-dessus (cf. Résultat).
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie
Une solution possible :
AAV2_AFF: Choisir et appliquer une méthode générique
On commence par faire abstraction des données spécifiques, en particulier numériques ou alphanumériques, pour ne considérer que les variables associées. Puis on reformule l'énoncé avec les noms des variables en explicitant les données du problème et les résultats attendus.
S'abstraire des données spécifiques revient simplement ici à initialiser les variables
minetmaxde la fonctionrandom.randint(min,max)aux données du problème particulier.On cherche à tirer aléatoirement un nombre
dcompris entre 2 nombreminetmaxinclus.Pour le dé à 6 faces :
min = 1etmax = 6.AAV5_AFF: Répondre explicitement à la question posée
L'instruction de type affectation qui permet de répondre à la question posée est donnée dans l'interpréteur ci-dessous.
python : affectation-jeux-1.pyOutputAAV3_AFF: Choisir et appliquer une technique de vérification
On procèdera par jeux de tests. En effet, la fonction
random.randint(min,max)est une fonction d'un module standard de Python (le modulerandom) : il y a peu de doutes sur le fait qu'elle fonctionne correctement.On vérifiera simplement ici que le code proposé ne « sort » pas des valeurs inférieures à
minou supérieures àmaxen le testant plusieurs fois de suite ou, au contraire, « sort » bien de temps en temps les valeurs extrêmes autoriséesminetmax.C'est bien le cas : les nombres compris entre 1 et 6 « sortent bien » tous et ceci de manière aléatoire.
-
Tirage de cartes
Proposer une instruction de type « affectation » qui permettra de simuler le tirage d'une carte dans un jeu de 32 cartes.
Les cartes seront représentées par un numéro de 1 à 32 : il n'y a ni couleurs (pique, cœur, carreau, trèfle), ni figures (roi, dame, valet).
aide Pythoninstruction d'affectation
a = baffecte la valeur de l'expression
bà la variable de noma.nombres aléatoires (documentation Python)
import randommodule Python à importer pour manipuler des nombres aléatoires.
random.random()retourne un nombre réel aléatoirement compris entre
0inclus et1exclu.random.randint(min,max)retourne un nombre entier aléatoirement compris entre
minetmaxinclus.
Votre réponse :
AAV2_AFF: Méthode
Application de la méthode
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie AAV5_AFF: Résultat
Utiliser l'interpréteur Python ci-dessous pour programmer l'algorithme demandé.
python : essai.pyOutputAAV3_AFF: Vérification
Application de la technique
Si la technique proposée nécessite Python, on la mettra en œuvre dans l'interpréteur ci-dessus (cf. Résultat).
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie
Une solution possible :
AAV2_AFF: Choisir et appliquer une méthode générique
On commence par faire abstraction des données spécifiques, en particulier numériques ou alphanumériques, pour ne considérer que les variables associées. Puis on reformule l'énoncé avec les noms des variables en explicitant les données du problème et les résultats attendus.
S'abstraire des données spécifiques revient simplement ici à initialiser les variables
minetmaxde la fonctionrandom.randint(min,max)aux données du problème particulier.On cherche à tirer aléatoirement un nombre
dcompris entre 2 nombreminetmaxinclus.Pour le jeu de 32 cartes :
min = 1etmax = 32.AAV5_AFF: Répondre explicitement à la question posée
L'instruction de type affectation qui permet de répondre à la question posée est donnée dans l'interpréteur ci-dessous.
python : affectation-jeux-2.pyOutputAAV3_AFF: Choisir et appliquer une technique de vérification
On procèdera par jeux de tests. En effet, la fonction
random.randint(min,max)est une fonction d'un module standard de Python (le modulerandom) : il y a peu de doutes sur le fait qu'elle fonctionne correctement.On vérifiera simplement ici que le code proposé ne « sort » pas des valeurs inférieures à
minou supérieures àmaxen le testant plusieurs fois de suite ou, au contraire, « sort » bien de temps en temps les valeurs extrêmes autoriséesminetmax.C'est bien le cas : seuls les nombres compris entre 1 et 32 « sortent bien » tous et ceci de manière aléatoire.
-
Pile ou face
Proposer une instruction de type « affectation » qui permettra de simuler le jeu de « pile ou face ».
« Pile » sera représenté par 0 et « Face » par 1.
aide Pythoninstruction d'affectation
a = baffecte la valeur de l'expression
bà la variable de noma.nombres aléatoires (documentation Python)
import randommodule Python à importer pour manipuler des nombres aléatoires.
random.random()retourne un nombre réel aléatoirement compris entre
0inclus et1exclu.random.randint(min,max)retourne un nombre entier aléatoirement compris entre
minetmaxinclus.
Votre réponse :
AAV2_AFF: Méthode
Application de la méthode
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie AAV5_AFF: Résultat
Utiliser l'interpréteur Python ci-dessous pour programmer l'algorithme demandé.
python : essai.pyOutputAAV3_AFF: Vérification
Application de la technique
Si la technique proposée nécessite Python, on la mettra en œuvre dans l'interpréteur ci-dessus (cf. Résultat).
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie
Une solution possible :
AAV2_AFF: Choisir et appliquer une méthode générique
On commence par faire abstraction des données spécifiques, en particulier numériques ou alphanumériques, pour ne considérer que les variables associées. Puis on reformule l'énoncé avec les noms des variables en explicitant les données du problème et les résultats attendus.
S'abstraire des données spécifiques revient simplement ici à initialiser les variables
minetmaxde la fonctionrandom.randint(min,max)aux données du problème particulier.On cherche à tirer aléatoirement un nombre
dcompris entre 2 nombreminetmaxinclus.Pour le jeu de « pile ou face » :
min = 0etmax = 1.AAV5_AFF: Répondre explicitement à la question posée
L'instruction de type affectation qui permet de répondre à la question posée est donnée dans l'interpréteur ci-dessous.
python : affectation-jeux-3.pyOutputAAV3_AFF: Choisir et appliquer une technique de vérification
On procèdera par jeux de tests. En effet, la fonction
random.randint(min,max)est une fonction d'un module standard de Python (le modulerandom) : il y a peu de doutes sur le fait qu'elle fonctionne correctement.On vérifiera simplement ici que le code proposé ne « sort » pas des valeurs inférieures à
minou supérieures àmaxen le testant plusieurs fois de suite ou, au contraire, « sort » bien de temps en temps les valeurs extrêmes autoriséesminetmax.C'est bien le cas : seuls les nombres 0 et 1 « sortent bien » tous les deux et ceci de manière aléatoire.
-
Prix de vente
Un libraire propose une réduction de 3.5% sur le prix hors taxes (HT) d'un livre à 12.35 € HT. Sachant que la taxe sur la valeur ajoutée (TVA) sur les livres est de 5.5%, proposer une instruction de type « affectation » qui permettra de calculer le prix de vente final pour le client.
aide Pythoninstruction d'affectation
a = baffecte la valeur de l'expression
bà la variable de noma.
Votre réponse :
AAV2_AFF: Méthode
Application de la méthode
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie AAV5_AFF: Résultat
Utiliser l'interpréteur Python ci-dessous pour programmer l'algorithme demandé.
python : essai.pyOutputAAV3_AFF: Vérification
Application de la technique
Si la technique proposée nécessite Python, on la mettra en œuvre dans l'interpréteur ci-dessus (cf. Résultat).
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie
Une solution possible :
AAV2_AFF: Choisir et appliquer une méthode générique
On commence par faire abstraction des données spécifiques, en particulier numériques ou alphanumériques, pour ne considérer que les variables associées. Puis on reformule l'énoncé avec les noms des variables en explicitant les données du problème et les résultats attendus.
Ainsi, on ne s'intéressera pas à la valeur « 12.35 € » mais à ce qu'elle qualifie : c'est-à-dire le prix hors taxes du livre, le « livre » étant lui-même un cas particulier de produit. Et ainsi pour chaque donnée spécifique du problème posé à laquelle on attribuera un nom.
Il s'agit donc ici de proposer une instruction de type « affectation » qui permettra de calculer le prix de vente (noté
pv) d'un produit connaissant son prix HT (notéht), la TVA (notéetva, exprimée sous la forme d'un pourcentage) sur ce type de produit et la réduction éventuelle (notéer, exprimée sous la forme d'un pourcentage du prix HT) proposée par le vendeur sur ce produit.reduction = ht*r/100
Sachant qu'une réduction se soustrait du prix HT initial pour obtenir le prix hors taxe effectivement proposé (noté
htr) :htr = ht - reduction
et qu'une taxe se calcule sur le prix hors taxe réellement effectué et s'ajoute à ce prix hors taxes, on a ainsi l'algorithme recherché :
taxe = htr*tva/100 pv = htr + taxe
algorithme qu'il faut initialiser avec les données du problème particulier :
ht, tva, r = 12.35, 5.5, 3.5
AAV5_AFF: Répondre explicitement à la question posée
L'instruction de type affectation qui permet de répondre à la question posée est donnée dans l'interpréteur ci-dessous.
python : affectation-elem-1.pyOutputAAV3_AFF: Choisir et appliquer une technique de vérification
On peut utiliser une méthode d'encadrement du résultat en encadrant le prix de vente \(p_v\) par 2 valeurs limites facilement identifiables : \(min \leq p_v \leq max\).
Le prix final sera en effet supérieur à la taxe imposée et inférieur au prix TTC sans réduction. On doit donc vérifier :
taxe <= pv <= ht*(1+tva/100)
On peut également utiliser une valeur évidente que doit donner l'algorithme : ici une réduction de 100% doit donner un prix de vente nul. Ainsi, pour \(r = 100\), on doit vérifier :
pv == 0
-
Conversion d'unités
On veut convertir 3.2 noeuds (nd, miles nautiques par heure) en kilomètres par heure (km/h).
Proposer une instruction de type « affectation » qui permettra de réaliser cette conversion d'unités.
- Lien utile :
National Institute of Standards and Technology guide for the use of the International System of Units (NIST), Annexe B9 (velocity)
rappels sur les unités en physique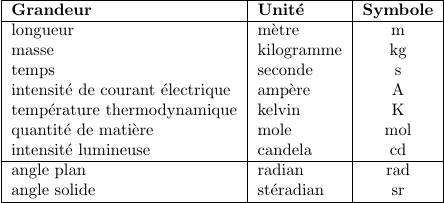
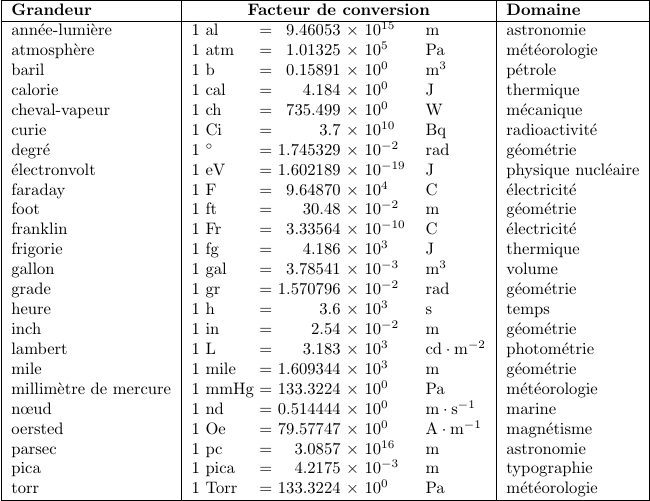aide Pythoninstruction d'affectation
a = baffecte la valeur de l'expression
bà la variable de noma.
Votre réponse :
AAV2_AFF: Méthode
Application de la méthode
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie AAV5_AFF: Résultat
Utiliser l'interpréteur Python ci-dessous pour programmer l'algorithme demandé.
python : essai.pyOutputAAV3_AFF: Vérification
Application de la technique
Si la technique proposée nécessite Python, on la mettra en œuvre dans l'interpréteur ci-dessus (cf. Résultat).
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie
Une solution possible :
AAV2_AFF: Choisir et appliquer une méthode générique
On commence par faire abstraction des données spécifiques, en particulier numériques ou alphanumériques, pour ne considérer que les variables associées. Puis on reformule l'énoncé avec les noms des variables en explicitant les données du problème et les résultats attendus.
Ainsi, on ne s'intéressera pas à la valeur « 3.2 nd » mais à ce qu'elle qualifie : c'est-à-dire une vitesse en noeuds, le « noeud » étant lui-même un cas particulier d'unité de vitesse. Et ainsi pour chaque donnée spécifique du problème posé à laquelle on attribuera un nom.
On cherche donc ici à convertir \(n_1\cdot u_1\) en \(n_2\cdot u_2\) où \(u_1\) et \(u_2\) sont des unités physiques compatibles qui dérivent de la même unité de base \(u_b\) du Système international d'unités.
\[\left| \begin{array}{l} u_1 = a_1\cdot u_b \\ u_2 = a_2\cdot u_b \end{array} \right. \Rightarrow \left| \begin{array}{l} n_1\cdot u_1 = n_1\cdot (a_1\cdot u_b) = (n_1\cdot a_1)\cdot u_b \\ n_2\cdot u_2 = n_2\cdot (a_2\cdot u_b) = (n_2\cdot a_2)\cdot u_b \end{array} \right. \Rightarrow \frac{n_1\cdot u_1}{n_2\cdot u_2} = \frac{n_1\cdot a_1}{n_2\cdot a_2}\]Comme on cherche \(n_2\) tel que \(n_1\cdot u_1 = n_2\cdot u_2\), on a donc :
\[\frac{n_1\cdot u_1}{n_2\cdot u_2} = \frac{n_1\cdot a_1}{n_2\cdot a_2} = 1 \Rightarrow n_2 = n_1 \cdot \frac{a_1}{a_2}\]où les coefficients \(a_i\) sont documentés dans le Système international d'unités par le Bureau international des poids et mesures (voir par exemple l'Annexe B9 (velocity) du NIST).
AAV5_AFF: Répondre explicitement à la question posée
Pour convertir 3.2 noeuds en kilomètres par heure, on utilise la séquence d'affectations proposée dans l'interpréteur ci-dessous.
python : affectation-elem-2.pyOutputAAV3_AFF: Choisir et appliquer une technique de vérification
On procèdera par jeux de tests en comparant les valeurs obtenues par le calcul avec celles de quelques valeurs caractéristiques connues ou facilement évaluables « à la main ».
Exemples :
- \(n_1 = 1.\mathrm{nd} \Rightarrow{} n_2 = 1.852 \mathrm{km/h}\)
- \(n_1 = 1./1852 \mathrm{nd} \Rightarrow{} n_2 = 1./1000 \mathrm{km/h} = 0.001 \mathrm{km/h}\)
On obtient bien les résultats escomptés avec Python.
-
Produit scalaire
On considère les 2 vecteurs \(\vec{A}\) et \(\vec{B}\) définis dans \(\mathbb{R}^2\) comme le montre la figure ci-dessous.
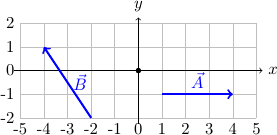
Proposer une instruction de type « affectation » qui permettra de calculer le produit scalaire \(\vec{A}\cdot\vec{B}\) de ces deux vecteurs.
aide Pythoninstruction d'affectation
a = baffecte la valeur de l'expression
bà la variable de noma.
Votre réponse :
AAV2_AFF: Méthode
Application de la méthode
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie AAV5_AFF: Résultat
Utiliser l'interpréteur Python ci-dessous pour programmer l'algorithme demandé.
python : essai.pyOutputAAV3_AFF: Vérification
Application de la technique
Si la technique proposée nécessite Python, on la mettra en œuvre dans l'interpréteur ci-dessus (cf. Résultat).
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie
Une solution possible :
AAV2_AFF: Choisir et appliquer une méthode générique
On utilise une représentation analytique. En effet, lorsque un objet est représenté sous une forme graphique, il est préférable de le transformer en sa représentation analytique (lorsqu'elle existe) pour étudier cet objet à l'aide d'un programme informatique.
Il s'agit ici de déterminer le produit scalaire \(\vec{V}_1\cdot\vec{V}_2\) de 2 vecteurs \(\vec{V}_1\) et \(\vec{V}_2\) de \(\mathbb{R}^2\) ayant pour composantes respectives \((x_1,y_1)\) et \((x_2,y_2)\).
Par définition, ce produit scalaire est un réel \(p\) qui a pour expression : \(p = x_1\cdot x_2 + y_1\cdot y_2\).
Ainsi, connaissant les composantes respectivement
(x1,y1)et(x2,y2)des vecteurs \(\vec{V}_1\) et \(\vec{V}_2\), on détermine le produit scalaireppar une affectation simple:p = x1*x2 + y1*y2
AAV5_AFF: Répondre explicitement à la question posée
Avant d'appliquer la formule précédente du produit scalaire, il faut initialiser correctement les composantes des 2 vecteurs.
python : affectation-elem-3.pyOutputAAV3_AFF: Choisir et appliquer une technique de vérification
On peut passer par une représentation géométrique en considérant l'interprétation géométrique du produit scalaire comme le rappelle la figure ci-dessous.
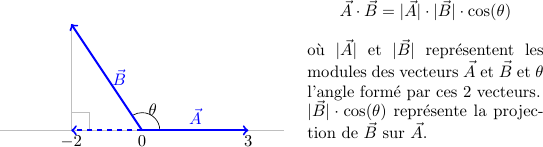
La projection de \(\vec{B}\) sur \(\vec{A}\) se lit très facilement sur la figure puisque \(\vec{A}\) est horizontal (parallèle à l'axe des abscisses avec \(|\vec{A}| = 3\)) : elle a pour valeur (-4) - (-2) = -2, d'où le produit scalaire \(p = 3 \cdot (-2) = -6\).
Le code Python précédent donne bien le même résultat.
-
Suite arithmétique
Proposer une instruction de type « affectation » qui permettra de calculer la somme \(s\) des \(n+1\) premiers termes \(u_k\) d'une suite arithmétique de premier terme \(u_0\) et de raison \(r\) : \(u_k = u_0 + kr\).
rappels mathématiquesLa somme arithmétique \(S = (1+2+\ldots\ +n)\) des \(n+1\) premiers entiers est telle que :
\(\begin{array}{rrccccccccccccc} & S &=& 1 &+& 2 &+& 3 &+& \ldots &+& (n-1) &+& n \\ + & S &=& n &+& (n-1) &+& (n-2) &+& \ldots &+& 2 &+& 1 \\ = & 2S &=& (n+1) &+& (n+1) &+& (n+1) &+& \ldots &+& (n+1) &+& (n+1)\\ \end{array}\)
On en déduit : \(S = \displaystyle\frac{n(n+1)}{2}\).
La somme géométrique \(S = (1 + q + q^2 + \ldots\ + q^n)\) de raison \(q \neq 1\) est telle que :
\(\begin{array}{rcccccccccccccc} S &=& 1 &+& q &+& q^2 &+& \ldots &+& q^{(n-1)} &+& q^n & & \\ qS &=& & & q &+& q^2 &+& \ldots &+& q^{(n-1)} &+& q^n &+& q^{(n+1)} \\ (1-q)S &=& 1 &+& 0 &+& 0 &+& \ldots &+& 0 &+& 0 &-& q^{(n+1)} \\ \end{array}\)
On en déduit : \(S = \displaystyle\frac{1-q^{(n+1)}}{1-q}\).
aide Pythoninstruction d'affectation
a = baffecte la valeur de l'expression
bà la variable de noma.
Votre réponse :
AAV2_AFF: Méthode
Application de la méthode
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie AAV5_AFF: Résultat
Utiliser l'interpréteur Python ci-dessous pour programmer l'algorithme demandé.
python : essai.pyOutputAAV3_AFF: Vérification
Application de la technique
Si la technique proposée nécessite Python, on la mettra en œuvre dans l'interpréteur ci-dessus (cf. Résultat).
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie
Une solution possible :
AAV2_AFF: Choisir et appliquer une méthode générique
On applique les résultats mathématiques sur les suites arithmétiques.
La somme \(s\) des \(n+1\) premiers termes d'une suite arithmétique \(u_k = u_0 + kr\) s'écrit :
\(s = u_0 + (u_0 + r) + (u_0 + 2r) + \ldots\ + (u_0 + nr) = (n+1)u_0 + r(1 + 2 + \ldots\ + n)\)
On pose \(S = (1 + 2 + \ldots\ + n)\). On a alors : \(s = (n+1)u_0 + rS\) où \(S\) est tel que :
\(\begin{array}{rrccccccccccccc} & S &=& 1 &+& 2 &+& 3 &+& \ldots &+& (n-1) &+& n \\ + & S &=& n &+& (n-1) &+& (n-2) &+& \ldots &+& 2 &+& 1 \\ = & 2S &=& (n+1) &+& (n+1) &+& (n+1) &+& \ldots &+& (n+1) &+& (n+1)\\ \end{array}\)
On en déduit : \(S = \displaystyle\frac{n(n+1)}{2}\) et donc \(\displaystyle s = (n+1)u_0 + r\frac{n(n+1)}{2}\)
L'application directe des résultats mathématiques concernant les sommes arithmétiques permet ainsi de proposer l'affectation suivante:
s = (n+1)*u0 + n*(n+1)*r/2
Il faut bien sûr connaître
n,u0etrpour évaluer cette somme.AAV5_AFF: Répondre explicitement à la question posée
python : affectation-prop-1.pyOutputAAV3_AFF: Choisir et appliquer une technique de vérification
On procèdera par jeux de tests en considérant par exemple la suite arithmétique bien connue des entiers naturels : \(u_0 = 0\) et \(r = 1\), pour laquelle la somme des \(n+1\) premiers entiers vaut : \(\displaystyle s = \frac{n(n+1)}{2}\).
Le code précédent est testé avec la somme des \(n = 5+1\) premiers entiers (\(u_0 = 0\) et \(r = 1\)). On a donc « à la main » : \(s = 0 + 1 + 2 + 3 + 4 + 5 = 15\), ce que donne l'exécution du programme Python.
-
Suite géométrique
Proposer une instruction de type « affectation » qui permettra de calculer la somme \(s\) des \(n+1\) premiers termes \(u_k\) d'une suite géométrique de premier terme \(u_0\) et de raison \(q\) : \(u_k = u_0q^k\).
rappels mathématiquesLa somme arithmétique \(S = (1+2+\ldots\ +n)\) des \(n+1\) premiers entiers est telle que :
\(\begin{array}{rrccccccccccccc} & S &=& 1 &+& 2 &+& 3 &+& \ldots &+& (n-1) &+& n \\ + & S &=& n &+& (n-1) &+& (n-2) &+& \ldots &+& 2 &+& 1 \\ = & 2S &=& (n+1) &+& (n+1) &+& (n+1) &+& \ldots &+& (n+1) &+& (n+1)\\ \end{array}\)
On en déduit : \(S = \displaystyle\frac{n(n+1)}{2}\).
La somme géométrique \(S = (1 + q + q^2 + \ldots\ + q^n)\) de raison \(q \neq 1\) est telle que :
\(\begin{array}{rcccccccccccccc} S &=& 1 &+& q &+& q^2 &+& \ldots &+& q^{(n-1)} &+& q^n & & \\ qS &=& & & q &+& q^2 &+& \ldots &+& q^{(n-1)} &+& q^n &+& q^{(n+1)} \\ (1-q)S &=& 1 &+& 0 &+& 0 &+& \ldots &+& 0 &+& 0 &-& q^{(n+1)} \\ \end{array}\)
On en déduit : \(S = \displaystyle\frac{1-q^{(n+1)}}{1-q}\).
aide Pythoninstruction d'affectation
a = baffecte la valeur de l'expression
bà la variable de noma.
Votre réponse :
AAV2_AFF: Méthode
Application de la méthode
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie AAV5_AFF: Résultat
Utiliser l'interpréteur Python ci-dessous pour programmer l'algorithme demandé.
python : essai.pyOutputAAV3_AFF: Vérification
Application de la technique
Si la technique proposée nécessite Python, on la mettra en œuvre dans l'interpréteur ci-dessus (cf. Résultat).
Zone de saisie de texte
Clavier Action F1 Afficher une aide technique F2 Afficher une aide pédagogique Ctrl-A Tout sélectionner Ctrl-C Copier la sélection dans le presse-papier Ctrl-V Copier le presse-papier dans la sélection Ctrl-X Couper la sélection et la copier dans le presse-papier Ctrl-Z Annuler la modification Maj-Ctrl-Z Rétablir la modification
Menu Action Ré-initialiser les sorties Faire apparaître le menu d'aide Valider la zone de saisie Initialiser la zone de saisie Charger le contenu d'un fichier dans la zone de saisie Sauvegarder le contenu de la zone de saisie dans un fichier Imprimer le contenu de la zone de saisie
Une solution possible :
AAV2_AFF: Choisir et appliquer une méthode générique
On applique les résultats mathématiques sur les suites géométriques.
La somme \(s\) des \(n+1\) premiers termes d'une suite géométrique \(u_k = u_0q^k\) avec \(q \neq 1\) s'écrit :
\(s = u_0 + u_0q + u_0q^2 + \ldots\ + u_0q^n = u_0(1 + q + q^2 + \ldots\ + q^n)\)
On pose \(S = (1 + q + q^2 + \ldots\ + q^n)\). On a alors : \(s = u_0S\) où \(S\) est tel que :
\(\begin{array}{rcccccccccccccc} S &=& 1 &+& q &+& q^2 &+& \ldots &+& q^{(n-1)} &+& q^n & & \\ qS &=& & & q &+& q^2 &+& \ldots &+& q^{(n-1)} &+& q^n &+& q^{(n+1)} \\ (1-q)S &=& 1 &+& 0 &+& 0 &+& \ldots &+& 0 &+& 0 &-& q^{(n+1)} \\ \end{array}\)
On en déduit : \(S = \displaystyle\frac{1-q^{(n+1)}}{1-q}\) et donc \(\displaystyle s = u_0\frac{1-q^{(n+1)}}{1-q}\)
L'application directe des résultats de mathématiques concernant les sommes géométriques permet de proposer l'affectation suivante:
s = u0*(1 - q**(n+1))/(1 - q)
Il faut bien sûr connaître
n,u0etq(avecq != 1) pour évaluer cette somme.AAV5_AFF: Répondre explicitement à la question posée
python : affectation-prop-2.pyOutputAAV3_AFF: Choisir et appliquer une technique de vérification
On procèdera par jeux de tests en considérant par exemple la suite des puissances de 2 : \(u_0 = 1\) et \(q = 2\), pour laquelle la somme des \(4+1\) premiers entiers vaut : \(\displaystyle s = \frac{1-2^5}{1-2} = 31\).
Le code précédent est testé avec la somme des \(n = 4+1\) premiers termes de la suite \(u_k = 2^k\). On a donc « à la main » : \(s = 2^0 + 2^1 + 2^2 + 2^3 + 2^4 = 1+2+4+8+16 = 31\), ce que donne l'exécution du programme Python.
-