4.2. Résolution#
Objectifs
Cette page de l’ENIBOOK participe à la zone généraliste de deuxième année
L’objectif est de réutiliser ce que vous avez appris concernant la boucle de simulation pour simuler le comportement d’un système modélisé avec des équations différentielles, dans le cadre de la ZG2.
Voir aussi
Un lien vers l’ancien cours : Séries temporelles
4.2.1. Ecrire dans un fichier CSV#
Lors de ce semestre en IPI, nous avons appris à programmer en utilisant une boucle de simulation et à mettre en œuvre une résolution d’Euler explicite. Cette méthode de programmation s’applique au développement d’un jeu en IPI mais peut évidemment s’appliquer à d’autres projets en programmation. Nous profitons donc de la zone généraliste pour appliquer à nouveau cette méthode.
Ainsi, vous pouvez vous fabriquer un outil réutilisable qui encapsule tout ce qu’il faut pour modéliser un système d’équations différentielles. Nous vous proposons une trame pour réaliser un code, mais bien évidemment, n’hésitez pas à personnaliser votre outil.
Puisque que nous avons défini un type TimeSeries lors de l’activité précédente, nous pouvons commencer par concevoir que le résultat de la simulation sera un TimeSeries.
Class : TimeSeries
data : liste de liste de réels
labels : liste de chaînes de caractères
À faire
Compléter time_series.py
Reprenez votre code de time_series.py que vous avez recodé en objet lors du cours de POO et ajoutez une méthode dump(self) qui crée un csv à partir d’un TimeSeries.
#!/usr/bin/python
# -*- coding: utf-8 -*-
'''Modules time_series.py provides Class TimeSeries in the context of ENIB ZG2 course'''
import csv
import matplotlib.pyplot as plt
__author__ = "Gireg Desmeulles"
__email__ = "desmeulles@enib.fr"
__version__ = "2.0"
class TimeSeries:
''' TimeSeries object allows to handle, plot, dump et load timeSeries for ZG2 project'''
#constructor
def __init__(self,filename=None,time_stamp_column_number=0):
self.__data=[]
self.__labels=[]
if filename :
with open(filename, newline='') as csvfile:
spamreader = csv.reader(csvfile, delimiter=',', quotechar='"')
for row in spamreader:
self.__data.append(row)
self.__labels=self.__data.pop(0)
if time_stamp_column_number:
self.swap_columns(0,time_stamp_column_number)
for line in self.__data:
for j in range(len(line)):
line[j]=float(line[j])
#accessors/mutators
def get_data(self):return self.__data[:]
def get_labels(self):return self.__labels[:]
def set_data(self,value): self.__data=value
def set_labels(self,value): self.__labels=value
#public methods
def swap_columns(self,c1,c2):
tmp=self.__labels[c1]
self.__labels[c1]=self.__labels[c2]
self.__labels[c2]=tmp
for line in self.__data :
tmp = line[c1]
line[c1]=line[c2]
line[c2]=tmp
#New method
def plot(self, x_label=None,y_label="",title="",filename=None, show=True):
nb_columns=len(self.__data[0])
# Data for plotting
columns = [[] for x in range(nb_columns)]
for line in self.__data:
for j in range(len(line)):
columns[j].append(line[j])
fig, ax = plt.subplots()
for i in range(nb_columns-1):
ax.plot(columns[0], columns[i+1], label=self.__labels[i+1])
ax.set(xlabel=x_label, ylabel=y_label,
title=title)
ax.legend()
ax.grid()
if filename:
fig.savefig(filename)
if show:
plt.show()
#New method
def dump(self,filename):
with open(filename, 'w', newline='') as csvfile:
spamwriter = csv.writer(csvfile, delimiter=',',)
spamwriter.writerow(self.__labels)
for line in self.__data:
output = []
for val in line:
output.append(str(val))
spamwriter.writerow(output)
if __name__ == '__main__':
t=TimeSeries(filename="HCSR04_data4_ressort_2022_03_10.csv",time_stamp_column_number=3)
t.plot(x_label='time (s)',y_label='distance(mm)',title='Courbe ZG2!!',filename='test.png')
t.dump('test.csv')
4.2.2. Un exemple d’équations différentielles du second ordre#
Voici un sujet de d’électronique que vous passerez peut-être lors des semestres suivants TDmoteur_temporel_S4A.pdf
On modélise le système suivant :

Voici l’équation différentielle :
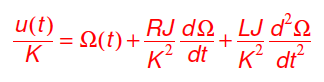
Le travail qui vous sera proposer dans ce TD d’électronique l’année prochaine, permettra de déterminer les différents paramètres de l’équation. Aujourd’hui, nous prendrons les valeurs suivantes pour la résolution numérique:
R = 0.5 Ohm
J = 0.0044 kgm2
L = 300 mH
K = 0.1 V.rad/s
u(t) = 10 V
À faire
Implémenter une classe pour représenter ce système
class Motor :
R : réels
J : réels
L : réels
K : réels
U : réels
omega0 : réels
omega1 : réels
omega2 : réels
- Cette classe fournit au moins deux opérations :
__init__(): un constructeur qui prend en paramètre les valeurs des paramètressimulate(self,sim_dt,log_dt,duration): une méthode que nous codrons dans un second temps.
4.2.3. Résoudre#
Il ne reste plus qu’a reprendre la méthode d’Euler explicite pour implémenter une méthode simulate().
- La méthode
simulate()prend en paramètres : le pas de simulation
le pas de trace
la durée de la simulation
La trace (log) est la liste des valeur que nous mémoriserons. Il n’est pas toujours de mémoriser toutes les valeurs simulées. Le pas de trace définit alors la précision à laquelle on mémorise les résultats.
La méthode simulate(self) renvoie un TimeSeries qui contient les séries temporelles de la vitesse du moteur et de ses dérivées premières et secondes.
4.2.4. Performances & précision#
Jouons avec le pas de simulation pour comprendre le compromis entre temps de simulation et erreur numérique…
À faire
Erreur numérique
Augmentez le pas de simulation jusqu’à observer des résultats de simulations aberrants. Puis baissez le pas de simulation jusqu’à constater que cela n’améliore plus les résultats de manière significative
À faire
Temps de calcul
Lorsque le pas de simulation devient petit, les temps de résolution deviennent importants. Il peut être intéressant de vérifier que votre code ne consomme pas inutilement du temps de calcul.
En utilisant Cprofile ou timeit(), essayez d’améliorer l’efficacité de la méthode simulate().
if __name__=="__main__":
#profilage
import cProfile
import timeit
m1=Motor()
m2=Motor()
m3=Motor()
#c_profile
cProfile.run('ts1=m2.simulate_slow(0.00001,0.001,7.0)')
cProfile.run('ts=m1.simulate(0.00001,0.001,7.0)')
cProfile.run('ts2=m3.simulate_fast(0.00001,0.001,7.0)')
#en utilisant timeit
print(timeit.timeit('m=Motor();ts1=m.simulate_slow(0.0001,0.001,7.0)',setup='from motor import Motor',number=20))