Lesson: Sensory-Motor Control
Today's Lesson
- Learning about sensory-motor control and PID control
- Writing code to enable vehicule to follow a line - here's a link to a sample solution for the line follower
Sensory-Motor Control and PID Control
One foundational concept in robotics is sensory-motor loops and control. The robot's sensor readings inform how it moves in its environment, which will then influence the next sensor readings from the robot, and the loop goes on. One of the most well known sensory-motor control methods is PID (Proportional Integral Derivative) control, which is depicted in the block diagram below:
The PID control function can be represented as follows:
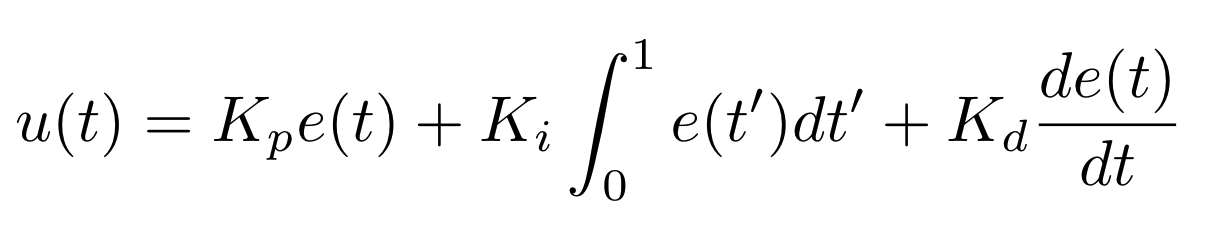
Where Kp, Ki, and Kd, are the constant coefficients for the proportional, integral, and derivative terms; e(t) represents the difference between the goal (setpoint) and the sensor measurement (process variable). The three following graphs display how a system responds to a step change in the setpoint to each component of the PID controller separately and all the components combined at different values of Kp, Ki, and Kd.

Response of the process variable to a step change of the setpoint for different values of Kp. Source: Wikipedia.
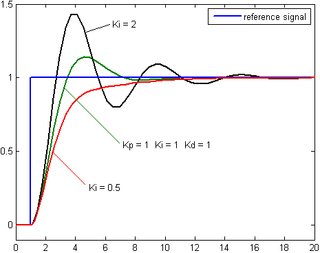
Response of the process variable to a step change of the setpoint for different values of Ki. Source: Wikipedia.
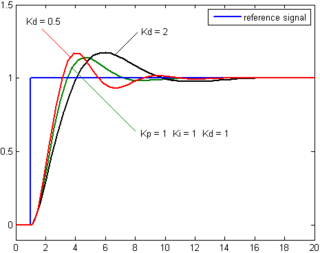
Response of the process variable to a step change of the setpoint for different values of Kd. Source: Wikipedia.
This YouTube video by Brian Douglas is a great resource providing a clear explanation of the PID controller.
Coding Exercise: Line Following
setup.py gazebo_lineFollow.launch.py camera_lidar_gazebo.urdf line_world.world launch_config.rviz
Getting Started
Considering, we have created iml_buche package :
$ ros2 launch iml_buche gazebo_lineFollow.launch.py
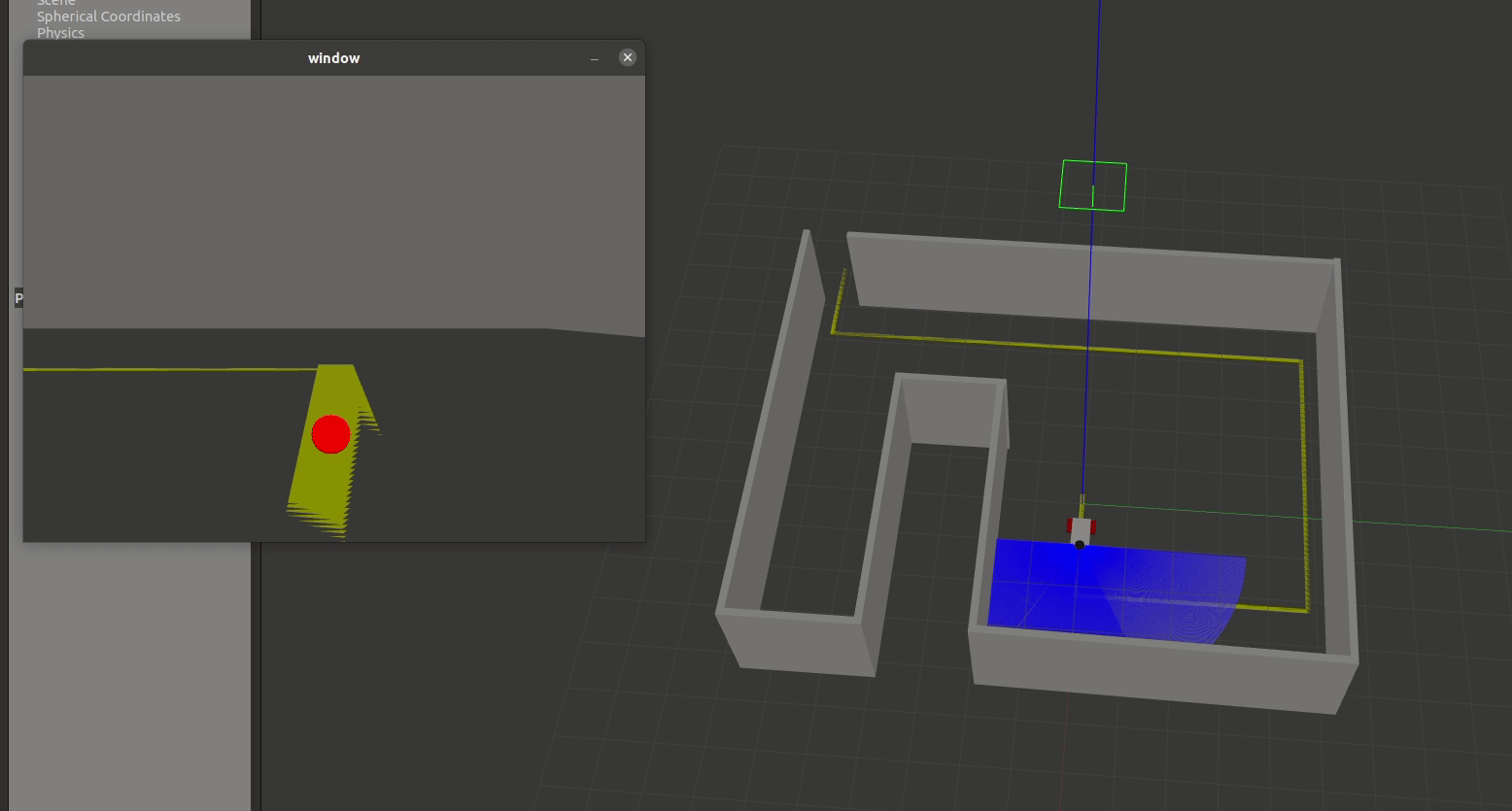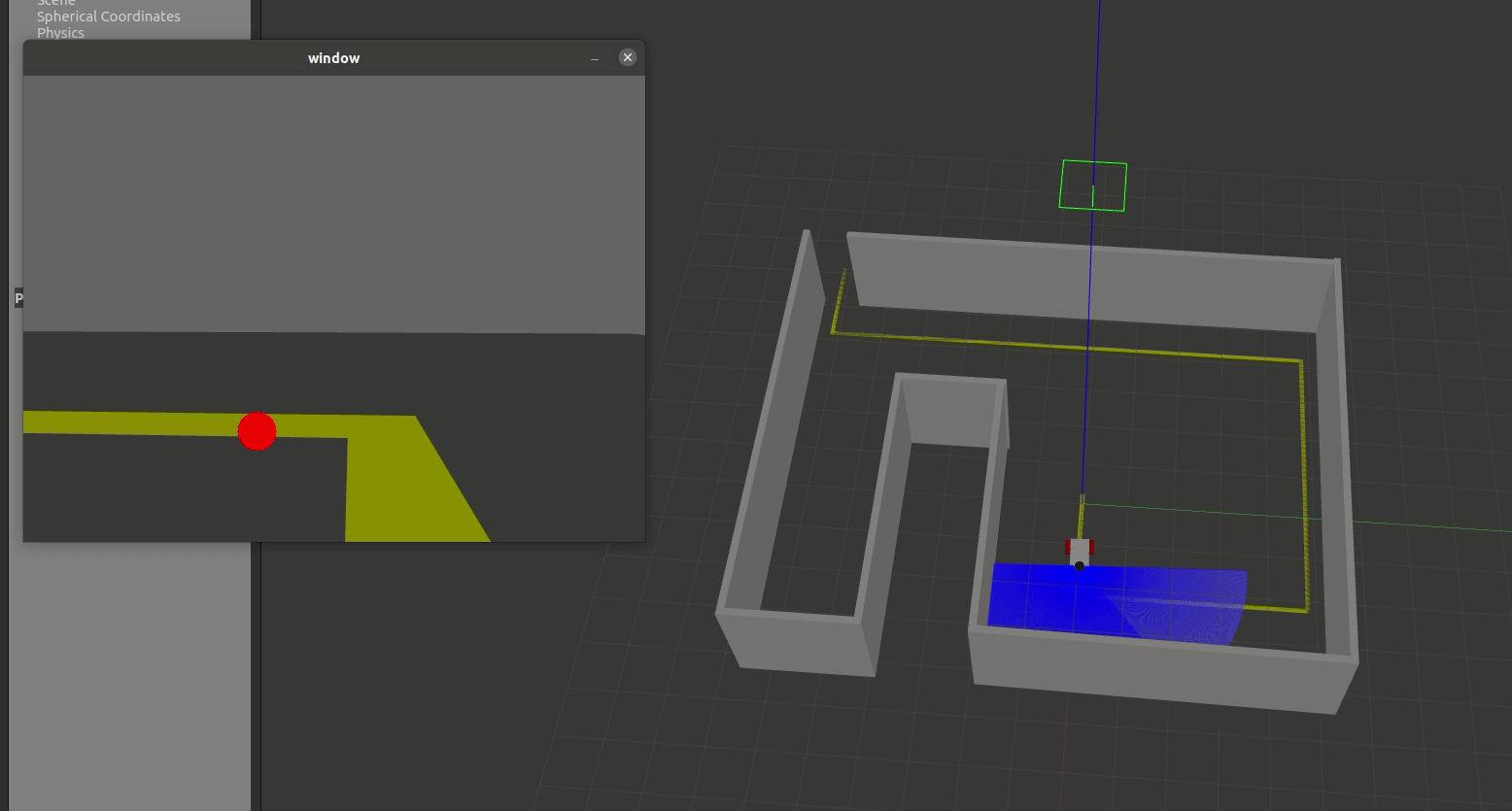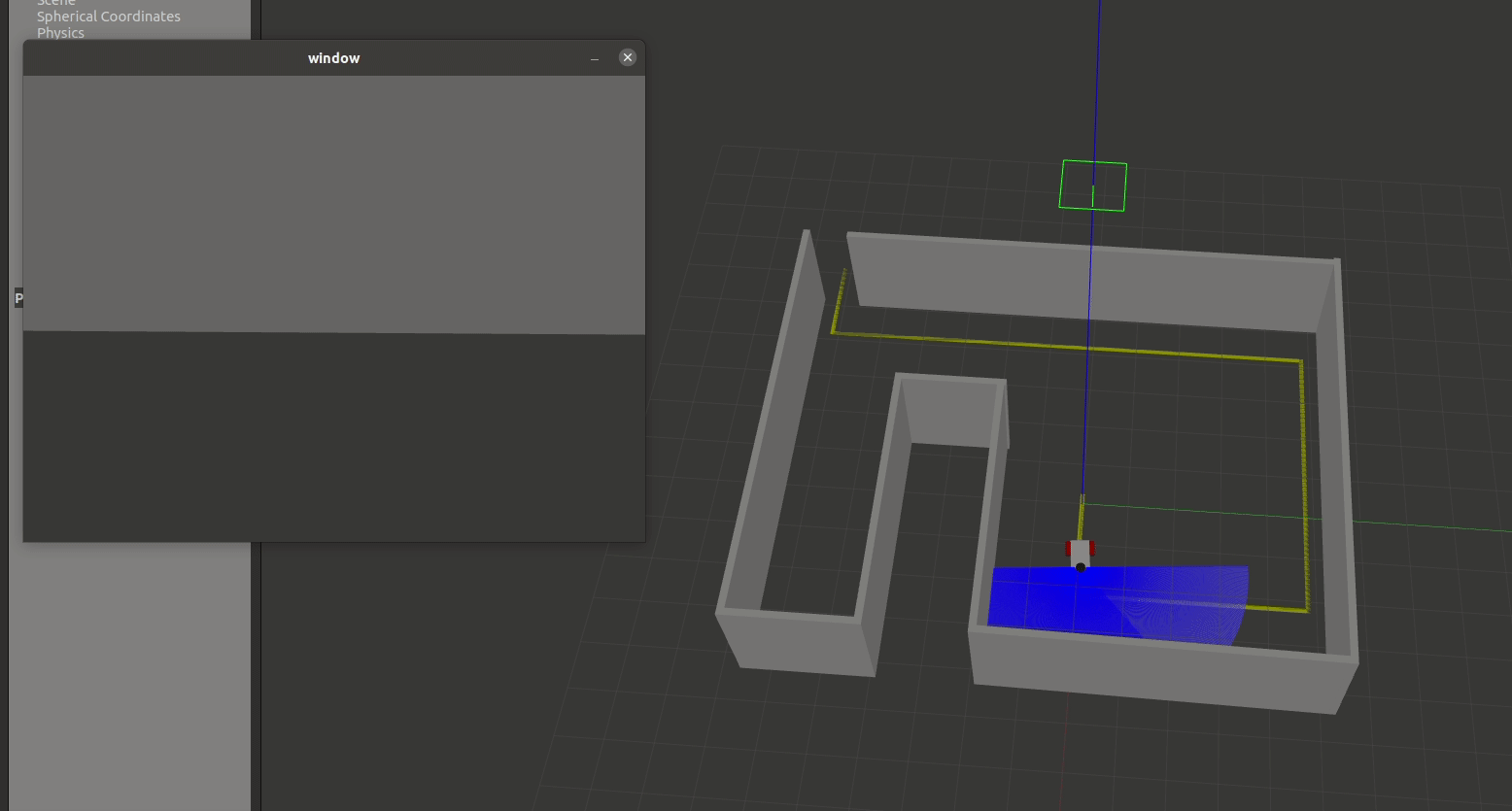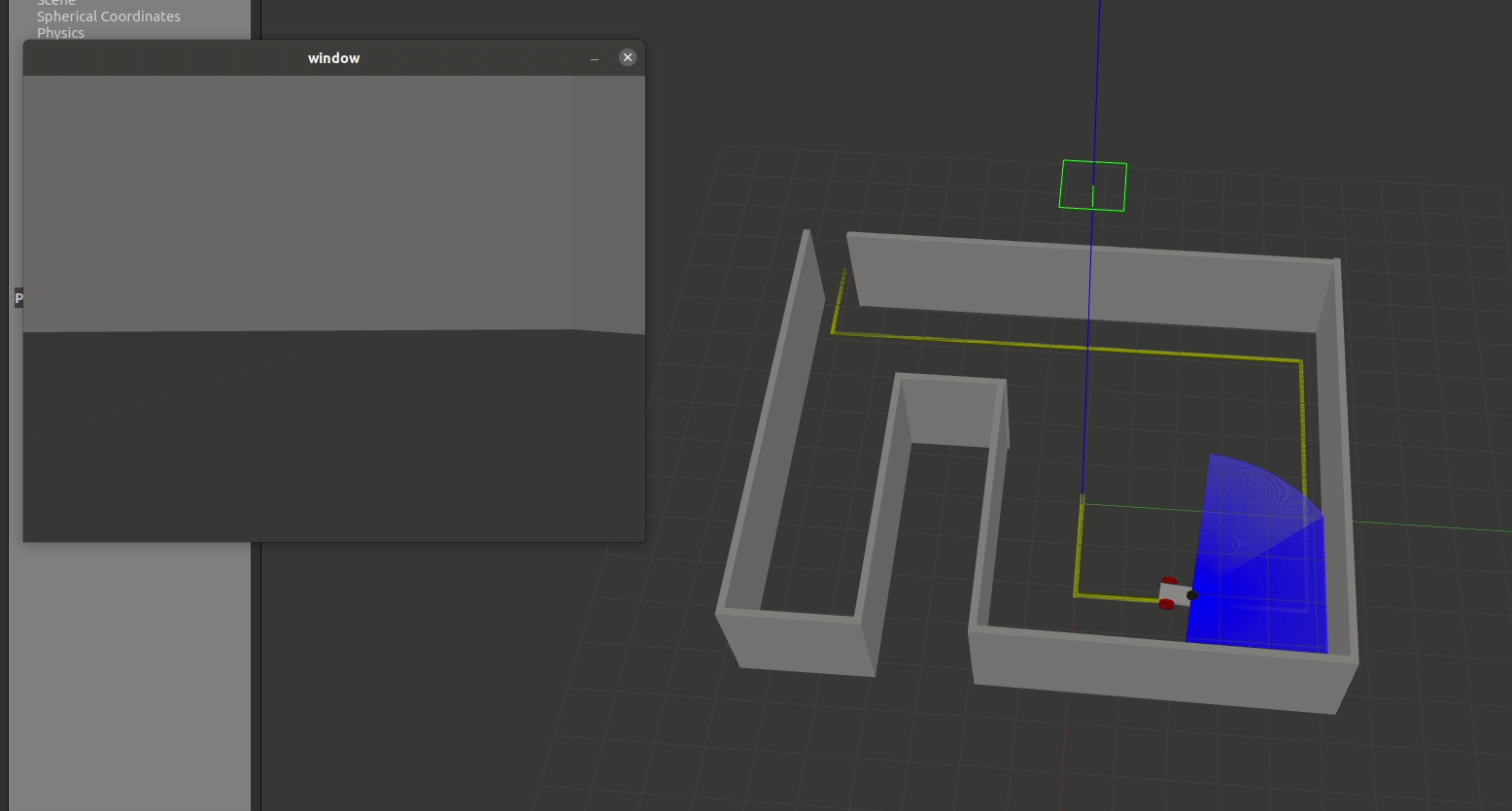
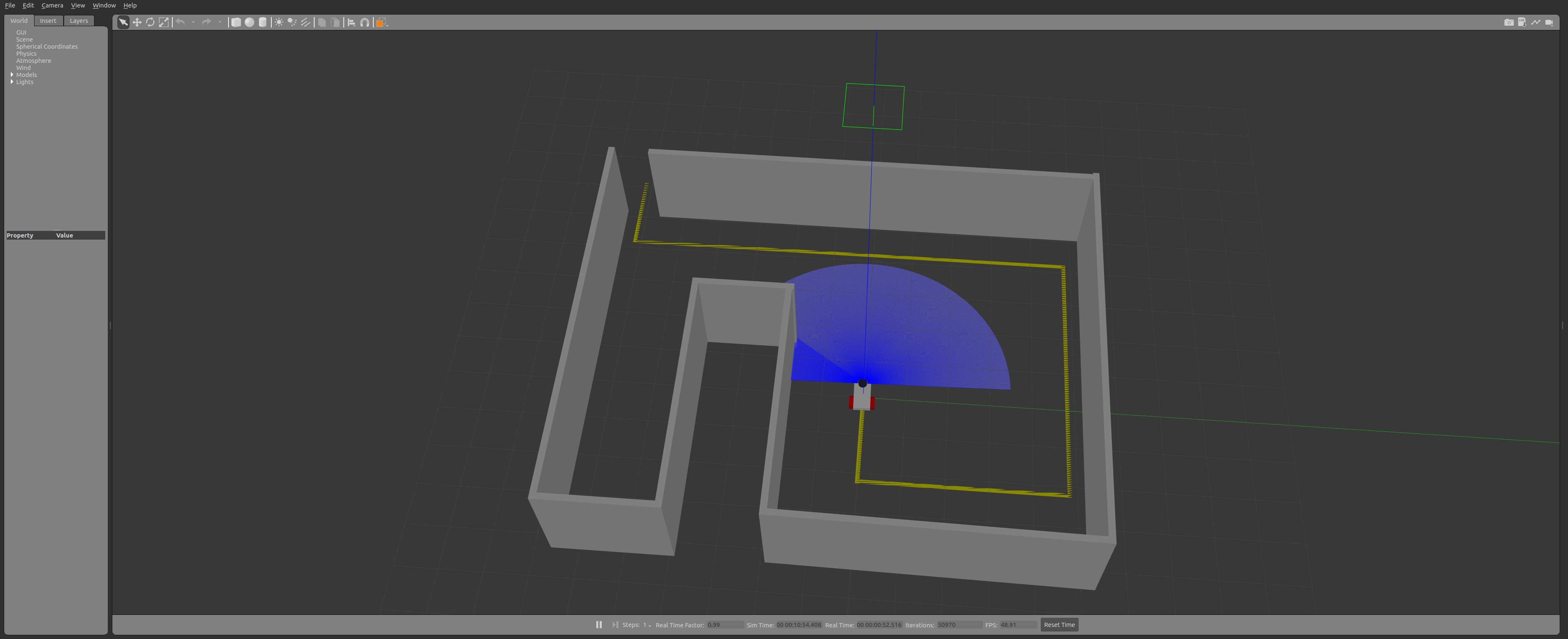
In Gazebo, you should see a vehicule at the beginning of a yellow line in an enclosed room (see image below). Your goal is to program the robot to follow the yellow line, writing your code in line_follower.py.
The starter code implements a helpful debugging window to help visualize the center of the computed yellow pixels. Once you've correctly identified the center of the yellow pixes, your window should look something like the following:

Understanding the Starter Code
Read through the starter code in line_follower.py. We encourage you to look up what certain OpenCV functions do to better understand what's going on. Make sure that you all discuss and understand what the following variables represent and what values they will hold: h, w, d, cx, cy.
Implementing the Line Follower
This programming exercise contains 2 main components:
-
Defining the range for what you will consider a "yellow" pixel in the image feed.
- OpenCV uses the following ranges for H, S, and V:
H: 0-179, S: 0-255, V: 0-255. As this OpenCV documentation suggests, you may find the following helpful (except you'll want to investigate yellow instead of green):green = np.uint8([[[0,255,0 ]]]) hsv_green = cv2.cvtColor(green,cv2.COLOR_BGR2HSV) print(hsv_green) -
You may also find the "Swatches" section on the HSV Wikipedia page helpful. Remember, you'll have to convert from the HSV ranges in the Wikipedia page
H: 0-360, S: 0.0-1.0, V: 0.0-1.0to the numeric ranges OpenCV expectsH: 0-179, S: 0-255, V: 0-255.- For example, the HSV Wikipedia color \(H = 60^{\circ}, S = \frac{1}{4}, V = \frac{5}{8}\) converts to the OpenCV HSV values of \(H = \big(\frac{60^{\circ}}{360^{\circ}} \cdot 180 - 1\big) = 29, S = \big(\frac{1}{4} \cdot 256 - 1\big) = 63, V = \big(\frac{5}{8} \cdot 256 - 1\big) = 159\)
- OpenCV uses the following ranges for H, S, and V:
-
Implementing proportional control to enable the robot to follow the yellow line. This will involve:
- Setting up a ROS2 publisher to control the movement of the robot.
- Computing an "error" term (the difference between the goal and the sensed reality). This most important part here is defining the "goal" and the "reality" comparison.
- Using the error term to determine how the robot moves in accordance with the principles of proportional control.
To run your code:
$ ros2 run iml_buche line_follower_modeOnce you've successfully implemented your proportional control line follower, it should look something like the following: